1. Простой процент: наращенная сумма, текущая стоимость, коэффициенты наращения и дисконтирования.

Простой процент определяется как произведение капитала, процентной ставки и времени: , где P – первоначальный капитал, j – номинальная годовая процентная ставка, t – срок депозита (в годах), I – простой процент (в денежном выражении). Сумма первоначального капитала и наросшего процента называется наращенной суммой (S). Итак, 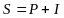. Наращенную сумму часто обозначают FV . Коэффициент наращения показывает наращенную сумму в расчете на одну денежную единицу первоначального капитала (.) .Приведенной (текущей) стоимость -первоначальный капитал, обеспечивающий наращенную сумму S, обозначают PV= Коэффициентом дисконтирования показывает текущую стоимость одной денежной единицы наращенной суммы, т.е. то количество денег, которое нужно положить на счет в настоящий момент времени для того, чтобы обеспечить одну денежную единицу наращенной суммы. Обозначаем буквой . Итак, .

2. Сложный процент: наращенная сумма, текущая стоимость, коэффициенты наращения и дисконтирования.

Процент называется сложным, когда после начисления процента начальный капитал вместе с наросшим процентом снова кладется на счет в банке, в следующем периоде времени процент нарастает не только с первоначального капитала, но также и с процента, наросшего в первом периоде. Наращенная сумма, . Время между двумя последовательными капитализациями (начислениями) процента называется периодом капитализации процента ,m- число капитализаций процента в течение года . Коэффициент наращения  (показывающий наращенную сумму в расчёте на одну денежную единицу первоначального капитала), находится по формуле: 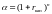. Текущая стоимость – это первоначальный капитал, обеспечивающий заданную наращенную сумму. . Коэффициент дисконтирования  (показывающий текущую стоимость в расчете на одну денежную единицу наращенной суммы). .

3. Смешанный метод начисления процентов при нецелом числе периодов капитализации: наращенная сумма, текущая стоимость, коэффициенты наращения и дисконтирования.

В соответствии со смешанным методом, вначале нужно найти наращенную сумму для целого числа периодов капитализации в сроке депозита. (Здесь через 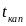обозначен срок депозита, выраженный в периодах капитализации. Заметим, что 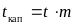.) Эта сумма находится по формуле для сложного процента: . Затем, для оставшейся дробной части срока депозита начисляется простой процент с капитала (наросшего за целое число периодов капитализации ). Заметим, что периода капитализации – это года. Следовательно, к концу срока депозита наращенная сумма составит: 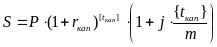. Учитывая, что , формулу можно также записать в виде: .

4. Общий метод начисления процентов при нецелом числе периодов капитализации: наращенная сумма, текущая стоимость, коэффициенты наращения и дисконтирования.

В соответствии с общим методом, наращенная сумма ищется по формуле ,где- S наращенная сумма, Р- первоначальный капитал, ,m- число капитализаций процента в течение года.