45. Построение трубопроводной характеристики. Статический напор. Потребный напор

статический напор – разница между уровнем воды во всасывающем резервуаре и высотой нагнетания как показано на схеме 2.1. Этот напор показан как H_s на схеме 2.2. В данном примере допускается, чтобы уровни воды в обоих резервуарах находились в условиях действия на них только атмосферного давления.

Вторая составляющая давления подачи насоса требуется для того, чтобы преодолеть трение потока жидкости, текущего по трубопроводу, клапанам, коленям и фитингам, которые находятся на пути от всасывающего резервуара к напорному. Это будет оцениваться исходя из того, что чем длинее труба, тем больше фитингов на ее пути, тем выше будут потери напора на трение. Напор, созданый насосом на выходе из напорного патрубка, должен быть с учетом преодоления трения на протяжение всей системы . Так как жидкость следует вдоль трубы, сумма трений на преодоление оставшегося своего пути постепеннно снижает скорость течения в трубопроводе и должна достигнуть значения «0» только после входа в напорный резервуар. Суммарные потери на трение показаны как H_f на схеме 2.2. Имея определенные H_s и Р_f , следующим шагом будет изобразить характеристики системы. Сделать это можно посчитав H_f для изменения расхода в системе. Несколько различных выбранных точек расхода достаточно для того, чтобы задать точки, на основе которых может быть построен график кривой. График системы кривых может быть построен при помощи суммарной высоты напора, Н_t в зависимости от расхода в системе где: Суммарная высота напора=Статический напор+Потери напора на трение или H_t=H_s+H_f нижняя отметка системы характеристик на оси Н это статический напор H_s. Это точка, в которой значение расхода равно «0». Затем наносится кривая с тенденцией возрастания значений суммарной высоты напора и расхода.

Потребный напор равен геометрическому напору плюс разность давлений на поверхности уровней в напорном и приемном резервуарах, плюс потери напора в системе на преодоление гидравлических сопротивлений.

Н тр=Нг+(р2-р1)/γ+(V2^2-V1^2)α^4/2g+∑hw

∑hw=(α*l/d+∑ξi)*V^2*2g

d=const

Hтр=Нст+kV^2

y=a+bx^2

Hтр=Hст+kQ^2/ω^2

46. Построение трубопроводной характеристики при парал и посл соедин корот трубопроводов

Послед.

Q1=Q2=Q3=Q (расход) ∑ hm-n=∑ h1+ ∑ h2+ ∑h3 (потери)

Парал.

Q=Q1+Q2+Q3

∑h1=Hm*Hn=∑h2=∑h3

∑h1=k1Q1m

∑h2=k2Q2m

∑h3=k3Q3m

Для постр хар-ки парал соед неск трубопр нужно сложить расходы хар-к этих трубопров при одинак ординатах ∑h

47.Расчёт длинных трубопроводов.Определение магистрали.Понятие коэф-та расхода.Построение трубопроводной характеристики в случае тупикового трубопровода.

Это трубопроводы постоянного по длине диаметра, у которых основными являются потери напора по длине, а местными потерями напора и скоростным напором можно пренебречь.

Потери напора по длине трубопровода определяют по формуле Дарси—Вейсбаха:

Учитывая, что расход Q = VЧS и скорость движения потока тогда

или

где А — удельное сопротивление трубопровода, определяемое по справочным таблицам;

Для переходной области удельное сопротивление Ао=А*b,

где b — поправочный коэффициент, учитывающий зависимость коэффициента гидравлического трения l от числа Рейнольдса.

Кроме удельного сопротивления А в литературе по гидравлике для решения задач приводится способ расчета длинных трубопроводов, базирующийся на формуле Шези.

Широко применяемые гидравлические параметры — это модуль расхода

сопротивление трубопровода ST=A*l, проводимость трубопровода

. С помощью вышеуказанных параметров потери напора по длине можно определить следующим образом:

Произведение ε и φ принято обозначать буквой и называть коэффициентом расхода, т.е. μ = εφ.

48.Выбор насоса, работающего на трубопроводную систему.Построение трубопроводной характеристики.Определение потребного напора.Поле насосов.Хар-ки насоса.Определение рабочей точки насоса.

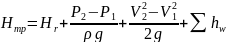
Подбор насоса осуществляется на основании построения трубопроводной хар-ки.

1)строим хар-ку

2)берём каталог насосов

По каталогу рассматриваем хар-ки насоса-кривые зависимости:

Это экспериментально полученные кривые зависимости.

Для построения трубопроводной хар-ки воспользуемся уравнением:

-высота подъёма жидкости от линии забора до макс.высоты;

-перепад давлений

потребный напор для обеспечения нужной подачи можно определить, составив уравнения Бернулли для характерных сече-

ний 0-0, 1-1 и 2-2

где hН и hВС - потери напора на нагнетательном и всасывающем участках.

Под напором насоса (H) понимается удельная механическая работа, передаваемая насосом перекачиваемой жидкости.

H = E/G [m]

E = механическая энергия [Н•м]

G = вес перекачиваемой жидкости [Н]

При этом напор, создаваемый насосом, и расход перекачиваемой жидкости (подача) зависят друг от друга. Эта зависимость отображается графически в виде характеристики насоса. Вертикальная ось (ось ординат) отражает напор насоса (H), выраженный в метрах [м]. Возможны также другие масштабы шкалы напора. При этом действительны следующие соотношения:

10 м в.ст. = 1 бар = 100 000 Па = 100 кПа

Точка, в которой пересекаются характеристики насоса и системы, является рабочей точкой системы и насоса. Это означает, что в этой точке имеет место равновесие между полезной мощностью насоса и мощностью, потребляемой трубопроводной сетью. Напор насоса всегда равен сопротивлению системы. От этого зависит также подача, которая может быть обеспечена насосом.

49. Гидродинамическое подобие - это подобие потоков несжимаемой жидкости, включающее в себя подобие геометрическое, кинематическое и динамическое.

Из геометрии известно, что геометрическое подобие означает пропорциональность сходственных размеров и равенство соответствующих угло в. В гидравлике под геометрическим подобием понимают подобие тех поверхностей, которые ограничивают потоки жидкости, Таким образом в гидравлике геометрическое подобие означает подобие русел или трубопроводов, по которым течёт жидкость.

Кинематическое подобие это подобие линий тока и пропорциональность сходственных скоростей. Это значит, что для кинематического подобия потоков требуется соблюдение геометрического подобия.

Динамическое подобие заключается в пропорциональности сил, действующих на сходственные элементы кинематически и геометрически подобных потоков, и равенство углов, характеризующих направление действия этих сил.

В потоках жидкостей (в нашем случае в трубопроводах, в гидромашинах и т.д.) обычно действуют разные силы – силы давления, силы вязкого трения, силы тяжести, инерционные силы. Соблюдение пропорциональности всех сил, действующих в потоке, означает полное гидродинамическое подобие.

На практике полное гидродинамическое подобие достигается редко, поэтому обычно приходится ограничиваться частичным (неполным) гидродинамическим подобием, при котором имеется пропорциональность лишь основных сил.

Записывается подобие следующим образом. Например, пропорциональность сил давления Р и сил трения Т, действующих в потоках I и II, можно записать в виде

.

-Критерий подобия Эйлера

При напорном движении идеальной несжимаемой жидкости для обеспечения гидродинамического подобия достаточно одного геометрического подобия. Безразмерная величина, представляющая собой отношение разности давлений к динамическому давлению (или разности пьезометрических высот к скоростной высоте), называется коэффициентом давления или числом Эйлера и обозначается Eu.

где - разность статических напоров

- Критерий подобия Рейнольдса

Для гидродинамического подобия геометрически и кинематически подобных потоков с учетом сил вязкости требуется равенство чисел Рейнольдса, подсчитанных для любой пары сходственных сечений этих потоков.

- Критерий подобия Фруда

В тех случаях, когда движение жидкости является безнапорным и происходит под действием разности нивелирных высот, условие подобия потоков описывается иначе, с помощью другого критерия подобия - числа Фруда. Этот критерий учитывает пропорциональность в отношениях сил инерции к силам тяжести. Однако для подавляющего большинства интересующих нас задач в области машиностроения этот критерий не имеет значения и рассматриваться не будет.

- Число Маха:

— скорость течения

— местная скорость распространения звука в движущейся среде

- Струхаля число

Критерий подобия нестационарных движений жидкостей или газов. Характеризует одинаковость протекания процессов во времени: ut = wl/u, где u — характерная скорость течения, l — характерный линейный размер, t — характерный для нестационарного движения промежуток времени, w — характерная частота (иногда через Sh обозначают обратную величину ut/l)

- Вебера

Мера соотношения сил инерции и поверхностного натяжения; отражает влияние последней на движение поток

50.

1. Гигроскопическая — в виде обособленных капелек располагается на частицах породы. Капельки плотно адсорбированы частицами породы и под влиянием молекулярных сил притяжения не в состоянии передвигаться в жидкой фазе. Отделиться от частиц по роды гигроскопическая вода может, только перейдя в газообразную форму. Ее можно удалить из породы путем нагрева последней до 105.. 110° С.

2. Пленочная —в виде воды, образующей вокруг частицы породы сплошную пленку. Минимальная толщина пленки может быть равна сечению молекулы воды. Пленочная вода передвигается от частицы с толстой пленкой к частице с более тонкой пленкой в любом направлении, преодолевая гравитационные силы.

3. Капиллярная — содержащаяся в каналах породы, диаметр которых не превышает 1 мм. Эта вода находится под влиянием молекулярных сил и сил поверхностного натяжения. Поднимается она снизу вверх, т. е. в направлении, противоположном действию гравитационных сил.

4. Гравитационная — характеризуется свободной капельножидкой водой, которая перемещается в горных породах под влиянием и по направлению действия силы тяжести, т. е. сверху вниз. Появляется в порах более 1 мм в диаметре.

Tечение жидкости в трубопроводах различного сечения может происходить в условиях полного их заполнения, т. е. когда частицы жидкости соприкасаются с внутренней поверхностью трубопровода по всему периметру сечения. Опытом установлено, что давление жидкости в таком трубопроводе вдоль потока не остается постоянным. Такое движение называется напорным. Примером напорного движения является обычный водопровод.

Течение реальной жидкости может происходить в открытых руслах, желобах или трубопроводах при условии неполного затопления труб, т. е. когда частицы жидкости соприкасаются с внутренней поверхностью трубопровода не по всему периметру сечения, а только по части периметра %. В этом случае в верхней части потока образуется свободная поверхность жидкости и давление вдоль потока остается постоянным. Такое движение жидкости называется безнапорным. Примером безнапорного движения может служить течение воды в естественных потоках, желобах, а также в трубопроводах канализационных сетей.

29.Определение коэффициентов местных сопротивлений для внезапного и плавного расширения, внезапного и плавного сужения, поворота трубы на 90 град.

Внез. Расширение:

ζ_р=(1-(ω1/ω2))²

Внез.сужение:

ζ_с=(1-ω2/ω1).0,5

ф-ла Идемчика

Плавное расширение:

ζ=К_д.(1-(ω1/ω2))²

К_д—коэф. смягчения

Плавное сужение:

ζ=((1/ε)-1)^с.К_с

ε- коэф. сжатия

ε= ω_d/ω₂

Поворот на 90:

ζ₉₀=0,051+0,19d/R

ζ₁₈₀=(0,051+0,19d/R).2

30. Явление кавитации. Критическое число кавитации.

-это явление холодного кипения жидкости.

В сеч.1-1 V1 и P1

В сеч. 2-2 V2 и P2

V2>>V1

P2<<P1

Если значение давления в сеч 2 достигнет Р при данной t, то из жидкости начнут интенсивно выделятся пузырьки растворенных газов.

В сеч.3-3 V3<<V2

P3>>P2

Т.к .T >V пузырьки газов начинают схлопываться на поверхности , выбивая мол-лы металла, что вызывает эрозию материала. Образуется отверстие.

Количественной характеристикой кавитации является число кавитации:

(Каппа)Н=(Р₁-Р_н.п. )/((ρ.V₁)/2)

Если Н<Н_кр,то кавитации не будет.

37-38. Истечение жидкости через насадки

Насадок:

-внутренний

-наружный

1.Насадок Вентури-внешний цилиндрический насадок L=(3,5-7)d

Назначение насадка-увеличение расхода

Q₀<Q_в до 34%

Насадок Вентури увеличивает расход на 34 вследствие наличия зоны вакуума внутри насадка,что обуславливается сжатием струи вследствие изменения потенциальной энергии mgh на кинетическую mV²/2.

нНасадок может работать со срывом,если H₁>H_кр

H_кр=(p₁-p_н.п.)/(ρ_ж-g) =13 м

H₁=10м, то срыв невозможен.

Данные насадки применяются в качестве водовыпусков у основания плотин.

2.Насадок Борда.

Потери значительны

Q_B>Q_б>Q₀

3.Внешний сходящийся насадок.

V =

Насадок увеличивает скорость.

Данные коноидальные насадки вследствие уменьшения потерь увеличивают дальность струи

Диффузионный

Общее уравнение для определения скорости и расхода через насадок

V=µ_НW

ВНЕШНИЙ РАСХОДЯЩИИЙСЯ

ИНВЕРСИЯ-ЯВЛЕНИЕ ИЗМЕНЕНИЯ ПОПРЕЧНОЙ ФОРМЫ СТРУИ ЖИДКОСТИ ИЛИ ГАЗА,ВЫХОДЯЩЕЙВ ЖИДКОСТЬ ИЛИ ГАЗ ДРУГОЙ ПЛОСКОСТИ.

54.

Для гравитационной плотины наибольшее значение из проявлений фильтрации имеет фильтрационное давление на ее подошву, или так называемое фильтрационное противодавление, снижающее сопротивление плотины сдвигу. Уменьшение противодавления достигается устройством противофильтрационной завесы в основании у верховой грани плотины, а также устройством дренажа основания. Величина фильтрационного противодавления зависит от многих факторов: трещиноватости скалы и ее характера, условий выхода фильтрационного потока в нижний бьеф, плотности контакта плотины и скального основания, глубины и качества противофильтрационной завесы, наличия или отсутствия дренажа основания.

Противофильтрационные завесы выполняются, как правило, путем цементации буровых скважин. В неблагоприятных условиях (агрессивные воды) вместо цементного раствора нагнетается битум или асфальт, разогретый или холодный в виде эмульсии. В этих же условиях, но при наличии трещин значительных размеров, каверн (карстовых) или полостей применяют глинизацию скважин. Дренаж основания осуществляется обычно в виде ряда специальных дренажных скважин, закладываемых в нем на небольшом расстоянии от завесы.

Роль дренажа основания очень важна, там как он снижает фильтрационное противодавление, чего одна противофильтрационная завеса, не доходящая по глубине до водоупора, не в состоянии сделать. Выполнять дренажные скважины лучше из специальной галереи (потерны) в плотине, что позволяет контролировать его работу.

Гидродинамическая сетка фильтрации подземных вод представляет собой систему линий равного напора (гидроизогипс) и нормальных к ним линий тока. Построение такой сетки начинается обычно с проведения гидроизогипс грунтового потока в условиях эксплуатации водоза­борного сооружения. Для этого определяется :положение уровня подземных вод в различных точках пласта по всей области фильтрации. Эти точки могут располагаться по некоторой заданной сетке, которая должна сгущаться на участках расположения водозаборных скважин, а также вблизи характерных точек подземного потока (раздельных точек). Уровень подземных вод в фиксированных точках определяется аналитически (в простейших случаях) или с использованием разнообразных моделирующих и цифровых устройств, широко применяемых при гидрогеологических исследованиях. Далее, путем интерполяции известных значений уровня в точках строятся изолинии уровня подземных вод при работе водозабора. Выбирается какая-либо точка на одной из гидроизогипс с большим значением уровня, из этой точки восставляется пер­пендикуляр к ней (рис. 37,а). Далее на перпендикуляре находится точка, располагающаяся на середине расстояния между выбранной гидроизогипсой и соседней с ней с меньшим значением уровня; из этой точки опускается перпендикуляр на сосед­нюю гидроизогипсу, и его пересечение с этой гидроизогипсой дает точку, лежащую примерно на одной линии тока с выбран­ной вначале точкой.

С хемы к построению гидродинамической сетки:а — построение линий тока; б — фрагмент гидродинамической сетки; 1 — линии тока; 2 — гидроизогипсы; 3 — ячейки сетки; 4 — полоса тока

55.Метод электродинамической аналогии (ЭГДА) основан на аналогии

уравнений движения электрического тока и безвихревого (потенциально-

го) движения жидкости. Двумерное безвихревое течение и движение элек-

трического тока в плоском проводнике с постоянной удельной электро-

проводностью описываются уравнением Лапласа. Поэтому оказывается

возможным исследовать обтекание тел идеальной жидкостью на электри-

ческих моделях, причем для соблюдения подобия должны быть выполне-

ны следующие условия:

1) электрическая модель должна представлять изучаемую область

течения в некотором масштабе без геометрического искажения;

2) граничные условия для модели и натуры должны быть аналогич-

ны.

В этом случае эквипотенциали (линии равного значения потенциала

V) в электрическом поле V(х, у) = const соответствуют эквипотенциалям в

потоке жидкости φ(х, у) = const (здесь φ - функция скоростного потен-

циала), а силовые липни в электрическом поле соответствуют линиям -

тока в жидкости.

Для решения задач плоского потенциального обтекания в настоящее

время преимущественно используются модели, в которых в качестве элек-

тропроводного материала применяется бумага с графитовым покрытием.

Граничные условия таковы:

1. Вдали от обтекаемого тела, где не сказывается его искажающее

влияние на поток, на линиях, перпендикулярных вектору скорости w,

функция скоростного потенциала сохраняет постоянное значение: φ =

const. Опыт показывает, что это условие удовлетворяется на расстоянии от

обтекаемого тела около трех его продольных размеров. На модели (рис.3)

это условие достигается заделкой в графитированную бумагу прямолиней-

ных металлических шин перпендикулярно направлению набегающего по-

тока: так как электропроводность металла намного выше, чем бумаги с

графитовым покрытием, при подаче на шины разности потенциалов от

внешнего источника на бумаге между шинами устанавливается течение

электрического тока, соответствующее равномерному потоку жидкости.

В качестве единицы потенциала принимают напряжение, приложен-

ное к шинам. При этом принимают, что одна шина имеет потенциал V=

0%, а другая V = 100%. Тогда все измерения будут производиться в долях

от максимального падения напряжения между шинами.

2. На линиях тока, ограничивающих исследуемую область, и на по-

верхности обтекаемого тела функция скоростного потенциала не меняется

в направлении нормали к границе: дφ /дп = 0. На модели, чтобы выполнить

это условие, достаточно обрезать по этим линиям электропроводную бума-

гу, т. е. заменить проводник изолятором (воздухом). Поскольку электриче-

ский ток может течь только вдоль линий обреза, на этих участках и будет

выполняться требуемое условие - вектор скорости направлен по касатель-

ной.

Помимо линий равного потенциала φ = const, методом ЭГДА можно

построить также линии тока ψ(х, у) = const, т. е. линии, вдоль которых век-

торы скорости направлены по касательной. Эквипотенциали и линии тока

взаимно ортогональны. При построении семейства линий тока граничное

условие φ = const заменяется эквивалентным ему условием дψ/дп = 0, а

граничное условие дφ /дп = 0 заменяется эквивалентным ему условием ψ

= const. На электрической модели строят линии равного потенциала элек-

трического поля; но, в зависимости от выбора граничных условий, эти ли-

нии будут соответствовать в потоке жидкости или эквипотенциалям (ана-

логия «А»), или линиям тока (аналогия «В»). Сетка эквипотенциалей и ли-

ний тока, построенная на одном графике, называется гидродинамической

сеткой течения и дает полное представление о скоростном поле потока.

Метод ЭГДА позволяет также определить величину циркуляции Г,

м /с, входящей в формулу Жуковского для подъемной силы крыла еди-

ничной длины:

Ry = ρ w∞Г, Н/м, (8)

где ρ - плотность жидкости, обтекающей крыло, w∞ - скорость не-

возмущенного потока. Величина циркуляции зависит от формы профиля

крыла и угла атаки; ее определение аналитическими методами сложно.

Значительно проще определяется циркуляция методом ЭГДА.

1. Первым научным трудом о гидравлики можно считать трактат Архимеда плавающих телах" (250 г. до н.э.). На рубеже 16-17 веков Леонардо да Винчи написал исследование "О движении и измерении воды".Последующие главнейшие работы принадлежат Галилею, Торичелли Паскалю, Ньютону. Торичелли сформулировал главный закон истечения идеальной жидкости из отверстий, Паскаль установил закон о передаче давления внутри жидкости, Ньютон высказал гипотезу о внутреннем трении в жидкости.Но как самостоятельная наука гидравлика начала формироваться только после работ М.Ломоносова, Д Бернулли и Л.Эйлера. В18 веке были установлены основные законы гидравлики, ставшие ее основой.В 19 веке в области гидравлических исследований можно отнести работы французского ученого Шези - изучавшего равномерное движение жидкости Вентури - исследовавшего истечение через насадки; Вейсбиха- местные и путевые сопротивления; Базена- истечение жидкости через водосливы; О. Рейнольдса -режимы движения жидкости. Большую роль в развитии гидравлики (19 в.) сыграли русские ученые: И.С. Громек ( ур-« Громека для вихревого движения жидкости); Профессор Н. Е. Жуковский (рассмотрел явление гидравлического удара, разработал теорию о подъемной силе крыла).В наше время а современной инженерной гидравлике ведущая роль принадлежит академику Павлавскому Н.Н., который исследовал важные проблемы в области равномерного и неравномерного движения жидкости, разработал новые методы расчета фильтрации под гидротехническими сооружениями. Большой практический интерес представляют работы в области теории неравномерного движения Рахманова, Чертоусава, Чугаева, Леей.Крупные исследования турбулентного режима движения жидкости выполнены академиком Колмагоровым, учеными Великановым, и Гуржиенко.В случае понятие о единичной массовой силе совпадает с определением ускорения. Если жидкость, находится под действием только сил тяжести, то единичной силой является ускорение свободного падения: g=M_g/М.где M_g - масса жидкости. Если жидкость находится в сосуде, движущимся с некоторым ускорением а, то жидкость в сосуде будет обладать таким же ускорением (ускорением переносного движения): а=Mа/М. Поверхностные силы равномерно распределены по поверхности и пропорциональны площади этой поверхности. Эти силы, действуют со стороны соседних объёмов жидкой среды, твёрдых тел или газовой среды В общем случае и называется напряжением. Нормальная составляющая поверхностных сил называется силой давления Р, а напряжение (единичная сила) называется давлением): р=(Р/S)*S где S-площадь поверхности. Напряжение тангенциальной составляющей поверхностной силы(касательное напряжение г) определяется аналогичным образом (в покоящейся жидкости Т=0)r=T/SВеличина давления (иногда в литературе называется гидростатическим давлением) в системе СИ измеряется в Паскалях.1Па=1н/м².Поскольку эта величина очень мала, то величину давления принято измерять в мега-паскалях МПа 1МПа = 1* 10⁶Па.В употребляемой до сих пор технической системе единиц давление измеряется в технических атмосферах, ат,1 ат =1кг/см² = 0,1 МПа, 1 МПа = 10 ат. В технической системе единиц давление кроме технической атмосферы измеряется также в физических атмосферах, А 1А = 1.033 ат. Различают давление абсолютное, избыточное и давление вакуума. Абсолютным давлением называется давление в точке измерения, отсчитанное от нуля Если за уровень отсчёта принята величина атмосферного давления, то разница между абсолютным давлением и атмосферным называется избыточным давлением.Р_изб= Р_абс - Р_а.Если давление, измеряемое в точке ниже величины атмосферного давления, то разница между замеренным давлением и атмосферным называется давлением вакуума

Р_изб= Р_а – Р_в

2. Плотность и уд. вес .К основным физ свойствам жидкости относят те её св-ва, которые определяют особенности поведения жид-ти при её движении. Такими явл св-ва, хар-е её концентрацию жидкости в пространстве, свойства опред. процессы деформации жидкости, определ. велечину внутреннего трения в жидкости при её движении, поверхностые эффекты. Важнейшим физ свойством жидкости, опред ее концентрацию в пространстве, явл. ее плотность. Под плотностью понмаеться масса единицы объема жидкости: р= M/W.M -масса жидкости,W - объём, занимаемый жидкостью.В международной системе единиц СИ масса вещества измеряется а кг, объем жидкого тела в м³ , тогда размерность плотности жидкости а системе единиц СИ –кг/м³ В системе единиц СГС плотность жидкости измеряетсн и г/см ³ . Величины плотности реальных капельных жидкостей в стандартных условиях изменяются в системе единиц СИ в широких пределах от 700 кг/м ³ до 1600 кг/м³ а плотность ртути достигает 13550 кг/м , плотность чистой воды составляет 998 кг/м " В системе единиц СГС пределы изменения плотности жидкости от 0,7 а/см до 1.8 г/см³ плотность чистой воды 0,998 г/см. Величины плотности газов меньше плотности капельных жидкостей приблизительно на три порядка, т.а. в системе единиц СИ плотности газов при атмосферном давлении и температуре ⁰С изменяются в пределах от 0,09 кг/м ³ до 3,74 кг/м³ , плотность воздуха составляет 1,293 кг/м ³ Плотность капельных жидкостей и газов зависит от температуры и давления. Зави­симость величины плотности жидкости и газа при температуре отличной от 20 ⁰С определяется по формуле Д И. Менделеева:Р₁=р₂₀/(1+В(T-T₀)) где: р и р₂₀- плотности жидкости (газа) при температурах соответственно ГиГ₀=20^вС,В - коэффициент температурного расширения. Исключительными особенностями обладает вода, максимальная плотность которой отмечается при 4 ⁰С.Плотность капельных жидкостей в зависимости от давления может быть определена в соответствии с уравнением состояния упругой жидкости: р(р) = р_капе^{в(р-ркап)} ,где р_кап-плотность капельной жидкости при атмосферном давлении,В-коэффициент объёмного сжатия капельной жидкости.Плотность идеальных газов при давлениях отличных от атмосферного можно определить по известному закону газового состояния Менделеева-Клайперона. избыточное давление в жидкостях измеряется манометрами. Это весьма обширный набор измерительных прибором различной конструкции и различного исполнения.

3. Жидкостью в гидравлике называют физическое тело способное изменять свою форму при воздействии на нее сколь угодно малых сил. Различают два вида жидкостей: жидкости капельные и жидкости газообразные. Основной отличительной особенностью капельных и газообразных жидкостей является способность сжиматься (изменять объем) под воздействием внешних сил. Капельные жидкости трудно поддаются сжатию, а газообразные жидкости (газы) сжимаются довольно легко, т.е. при воздействии небольших усилий способны изменить свой объем в несколько раз. В гидравлике рассматриваются реальная и идеальная жидкости. Идеальная жидкость в отличие от реальной жидкости не обладает внутренним трением, а также трением о стенки сосудов и трубопроводов, по которым она движется. Идеальная жидкость также обладает абсолютной несжимаемостью. Такая жидкость не существует в действительности, и была придумана для облегчения и упрощения ряда теоретических выводов и исследований.

1 Па = 1 Н/м² = 10-3 кПа = 10-6 МПа.

За единицу давления в Международной системе единиц (СИ) принят паскаль - давление вызываемое силой 1 Н, равномерно распределенной по нормальной к ней поверхности площадью 1 м². Основные механические характеристики

Одной из основных механических характеристик жидкости является ее плотность. Плотностью жидкости называют массу жидкости заключенную в единице объема.

Основные физические свойства. Сжимаемость - свойство жидкости изменять свой объем под действием давления. Сжимаемость жидкости характеризуется коэффициентом объемного сжатия, который определяется по формуле

Т емпературное расширение - относительное изменение объема жидкости при увеличении температуры на 1°С при Р = const. Характеризуется коэффициентом температурного расширения

Силы поверхностного натяжения - эти силы стремятся придать сферическую форму жидкости. Силы поверхностного натяжения обусловлены поверхностными силами и направлены всегда внутрь рассматриваемого объема перпендикулярно свободной поверхности жидкости. Рассмотрим бесконечно малый объем жидкости на свободной поверхности. На него будут действовать силы со стороны соседних объемов. В результате, если сложить вектора всех сил действующих на рассматриваемый объем, то суммарная составляющая сила будет направлена перпендикулярно внутрь рассматриваемого объема. Вязкость жидкости - свойство жидкости сопротивляться скольжению или сдвигу ее слоев. Суть ее заключается в возникновении внутренней силы трения между движущимися слоями жидкости, которая определяется по формуле Ньютона

Испаряемость жидкости. Испаряемость свойственна всем капельным жидкостям, однако интенсивность испарения неодинакова у различных жидкостей и зависит от условий в которых она находится: от температуры, от площади испарения, от давления, и от скорости движения газообразной среды над свободной поверхностью жидкости (от ветра). Растворимость газов в жидкостях характеризуется объемом растворенного газа в единице объема жидкости и определяется по закону Генри:

4 . Гидростатика- это раздел гидравлики, в котором рассматр законы , действ в покоящихся жидкостях. В результ действ внешних сил внутри жидкости появляется напряжение. Сжимающее напряжение, возникающее внутри покоящейся жидкости наз гидростатическим давлением.

Св-ва гидростат давления. 1) Г/ст давл направлено всегда по внутренней нормали к площадке на кот это давление действует. Рассмотрим некот обьем жидкости, наход в равновесии. разделим разделим этот обьем плоскостью SS. На поверхн раздела возьмем точку А. в этой точке действ г/ст дав. предположим что давление Р направлено наклонно. Тогда Р можноразложить на 2 составл ее силы: Р и Р-касательную. Жидкость не может сопротивляться касат усилиям и частицы Ж под действ Р выйдут из равновесия, т е нарушиться основное условие о равновесии Ж=>предположение о наклонной силе не верно=>единственным направлением Р является направление по нормали. далее докажем что г/ст дав направлено только по внутренней нормали. Предположим что г/ст дав может быть направлено по внеш нормали. Однако эта растягивающая сила вызовет движение частиц жидк, поскольку идеальн Ж не оказывает сопротивление растягивающим усилиям, -> предположение не верно, поскольку противоречит исходному условию о нахождении Ж в покое. Г/ст дав может быть направлено только по внутренней нормали, т е внутрь Ж и явл сжимающим напряжением.

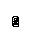
2) Величина г/ст давления в любой точке жидкости по всем направлениям одинакова. Выделим внутри жидкости элементарную призму.

Рассмотрим условие равновесия этой призмы под действием внешних сил:- поверхностные нормальные силы, действ на грани призмы. -обьемные силы, пропорциональные массе, т е силы тяжести. Следовательно г/ст давление в исследуемой точке А по всем направлениям одинаково.

3) Г/ст давление в точке зависит от ее координат в пространстве. Это очевидно, поскольку при погружении тела в глубину жидкости на него давит все более высокий столб жидкости, соответственно давление будет повышаться.