1.Определение временных рядов

Временно́й ряд (или ряд динамики) — собранный в разные моменты времени статистический материал о значении каких-либо параметров (в простейшем случае одного) исследуемого процесса. Каждая единица статистического материала называется измерением или отсчётом, также допустимо называть его уровнем на указанный с ним момент времени. Во временном ряде каждому отчету должно быть указано время измерения или номер измерения по порядку. Временной ряд существенно отличается от простой выборки данных, так как при анализе учитывается взаимосвязь измерений со временем, а не только статистическое разнообразие и статистические характеристики выборки^[1].

Примеры временных рядов:

Временные ряды, как правило, возникают в результате измерения некоторого показателя. Это могут быть как показатели (характеристики) технических систем, так и показатели природных, социальных, экономических и других систем (например, погодные данные). Типичным примером временного ряда можно назвать биржевой курс, при анализе которого пытаются определить основное направление развития (тенденцию или тренда).

2. Особенности представления и моделирования временных рядов.

Временной ряд – множество последовательных наблюдений, упорядоченных во времени по уровням состояния либо изменения некоторого изучаемого наблюдения (времени). (например: динамика продаж за неделю)

Отличие временного ряда от случайной выборки:

1. в общем случае члены временного ряда не являются статистически независимыми. y₁, y₂, … , y_N – статистические зависимые.

2. случайная величина члена временного ряда имеет различное распределение.

Временной ряд характеризуется средним значением M(y) и дисперсией D(y).

Динамика временного ряда может быть оценена множеством последовательностей:

• абсолютные приросты

• темпы прироста

• темпы роста

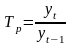
3. Методы анализа временных рядов

Временные ряды исследуются с различными целями. В одном ряде случаях бывает достаточно получить описание характерных особенностей ряда, а в другом ряде случаев требуется не только предсказывать будущие значения временного ряда, но и управлять его поведением. Метод анализа временного ряда определяется, с одной стороны, целями анализа, а с другой стороны, вероятностной природой формирования его значений.

Укажем самые распространенные методы анализа временных рядов.

Название метода	Характеристика метода
Спектральный анализ	Позволяет находить периодические составляющие временного ряда
Корреляционный анализ	Позволяет находить существенные периодические зависимости и соответствующие им задержки (лаги) как внутри одного ряда (автокорреляция), так и между несколькими рядами. (кросскорреляция)
Модели авторегрессии и скользящего среднего	Модели ориентированы на описание процессов, проявляющих однородные колебания, возбуждаемые случайными воздействиями. Позволяют предсказывать будущие значения ряда.
Многоканальные модели авторегрессии и скользящего среднего	Модели применяются в тех случаях, когда имеется несколько коррелированных между собой временных рядов. В них имеются колебания, возбуждаемые одной причиной. Позволяют предсказывать будущие значения ряда.
Сезонная модель Бокса-Дженкинса	Применяется , когда временной ряд содержит явно выраженный линейный тренд и сезонные составляющие. Позволяет предсказывать будущие значения ряда. Модель была предложена в связи с анализом авиаперевозок.
Прогноз экспоненциально взвешенным скользящим средним	Простейшая модель прогнозирования временного ряда. Применима во многих случаях. В том числе, охватывает модель ценообразования на основе случайных блужданий.