2) Заложение, превышение, интервал и уклон прямой.

На черт. изображена прямая АВ и её проекция А₁В₃ на основную пл-ть П₀.

Длина горизонтальной пр-ии a b называется заложением отрезка прямой и обозначается буквой L.

Разность отметок концов отрезка прямой наз-ся превышением (подъёмом) отрезка и обозначается Н

Разделив прямую АВ на равные отрезки, получим т-ку D с отметкой 2: D₂.

Если разность отметок двух т-ек прямой равна единице, то заложение отрезка прямой, определяемого этими т-ми, наз-ся интервалом прямой и обозначается ℓ.

Иными словами, интервал прямой - это заложение, соответствующее подъёму, равному единице.

ℓ=L/Н; (1)

L – заложение;

Н – превышение (подъём);

ℓ - интервал заложения, приходящийся на единицу превышения.

Уклон прямой определяется тангенсом угла наклона прямой к плоскости уровня.

i = tg  ( - угол наклона прямой к пл-ти П₀).

Уклоном прямой называется отношение превышения прямой к её заложению.

tg  = Н/ L = 1 / ℓ, i = 1 / ℓ (2)

Из равенства следует, что уклон линии является величиной, обратной её интервалу.

Уклон и интервал прямой могут быть вычислены при помощи равенств (1) или (2) или определены графически, при помощи совмещения прямой с плоскостью П₀ и выполнения построений, рассмотренных выше.

Понятия уклон и интервал используются для характеристики продольного профиля пути, крутизны откосов насыпей и выемок

Билет№23

1) Определить НВ отрезка АВ вращением вокруг проецирующей оси.

Р ешение:

2) Градуирование прямой – нахождение на пр-и прямой т-ек, имеющие целые числовые отметки.

Градуирование основано на способе пропорционального деления отрезка прямой линии.

Задача 1. Проградуировать прямую АВ, заданную проекцией

А₂₀ В₂₇ .

Решение:

Задачу решают, используя теор. Фалеса. Проводим через т-ку В в произвольном направлении линию и откладываем на ней через равные промежутки отрезки с 21 до 27. Затем соединяем т-ку 27 с т-кой А₂₇. ||-но полученному отрезку прямой проводим прямые от т-ек 21 – 26. Эти прямые пересекут отрезок АВ в определённых т-ках, которые и делят саму прямую АВ на равные прмежутки от 20 до 27. таким образом, мы проградуировали прямую АВ.

Решим такую же задачу другим способом.

Задача 2. Проградуировать прямую АВ, заданную проекцией

a_16,5 b_13,5 .

Решение:

Необходимо определить на пр-ии данной прямой положение пр-ий т-ек с отметками 16, 15, 14.

| |-но проекции прямой А_16,5 В_13,5 проведём ряд прямых, отстоящих друг от друга на равном расстоянии произвольной величины, и примем их за линии уровня с отметками 13, 14, 15, 16, 17. На прямых ,  - ных к проекции данной прямой и проведённых через точки А_16,5 В_13,5 , отметим соответственно точку А' на уровне 16,5 и точку В' - на уровне 13,5 , затем соединим их прямой линией. Точки пересечения этой прямой с линиями уровня будут иметь отметки 14, 15, 16. Основания  - ров, опущенных из этих точек на проекцию прямой, и будут проекциями точек, имеющих целые отметки 14, 15, 16. Очевидно, что эти точки и делят проекцию прямой на равные отрезки.

Описанный способ градуирования прямой при помощи || - ных прямых, проведённых на равных расстояниях друг от друга, положен в основу «палетки», применяемой при наводке горизонталей рельефа местности на картах и планах.

Билет№24

1) Определить НВ Δ АВС вращением вокруг проецирующих осей.

Р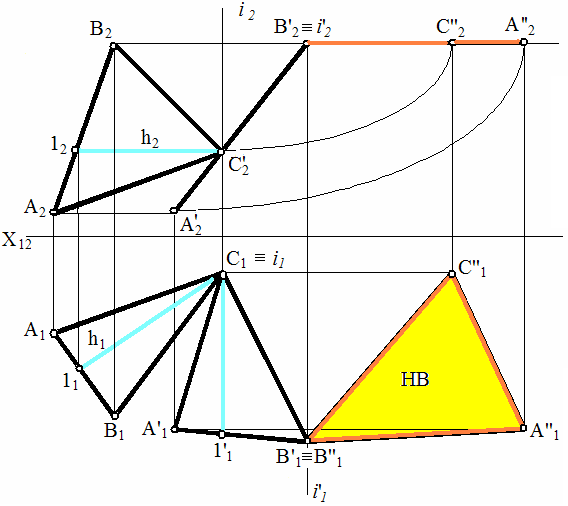 ешение:

2) Построить точку пересечения прямой А₄ В₇ с плоскостью, заданной масштабом уклонов ∑_i .

Алгоритм решения задачи такой же, как на эпюре Монжа:

1. Через прямую необходимо провести вспомогательную пл-ть общего положения Г.

2. Г ∩ Р Þ СD

3. СD ∩ АВ Þ К

1. Проводим через прямую АВ плоскость-посредник Г общего положения. Градуируем прямую АВ. Далее в любом направлении, но взаимно ||-но проводим горизонтали плоскости-посредника Г от точек А и В.

2. Находим линию пересечения одноимённых горизонталей плоскостей Г_i и ∑_i - это линия СD.

3. Проекцией искомой точки пересечения прямой с плоскостью ∑_i будет точка К - точка пересечения прямой АВ и прямой СD.

Билет№25

1) Теорема о прямом угле.

Если одна сторона прямого угла параллельна какой-либо плоскости пр-ий, а другая сторона не перпендикулярна к ней, то на эту плоскость пр-ий прямой угол проецируется в НВ

Если две прямые пересекаются под прямым углом, то проекции их в общем случае образуют угол, не равный 90⁰.

Для того, чтобы прямой угол проецировался в НВ, необходимо и достаточно, чтобы одна из его сторон была ||-на, а другая не -на пл-ти пр-ий.

Действительно, пусть сторона АВ прямого угла АВС ||-на пл-ти П₁. требуется доказать, что проекция его: угол А₁В₁С₁ = 90⁰.

Прямая АВ -на пл-ти ∑, т.к. АВ -на двум прямым этой пл-ти ВС и ВВ₁, проходящим через т-ку В.

Прямая АВ и её пр-ия А₁В₁ – две ||-ые прямые, а потому А₁В₁ также -на пл-ти ∑. Следовательно, А₁В₁ -на В₁С₁.

2) Поверхности вращения (исключая конус и цилиндр) относятся к неразвёртываемым поверхностям. Для них строят условные развёртки, заменяя части этих поверхностей отсеками развёртываемых поверхностей.Это называется аппроксимацией.

Развёртка сферы и тора.

Суть построения состоит в том, что мы должны построить развёртку поверхности, разделив её на несколько долей (как апельсин). И, таким образом, строим развёртку одной доли, другие – её повторяют.

Итак, делим гор. пр-ию поверхности на 8 равных частей. Надо заметить, что развёртка получится тем точнее, чем на большее количество частей мы разделим поверхность.

Одну из частей делим снова пополам. Таким образом, получаем одну целую дольку. Будем строить её развёртку.

• На фронтальной пр-ии очерковую линию делим с помощью произвольно взятых точек (чем их >, тем точнее развёртка);

• Находим горизонт. пр-ии данных точек.

• Затем на свободном месте листа проводим горизонтальную линию - экватор сферы. Отмечаем произвольно некоторую точку 1;

Проводим через неё вертикальную линию ();

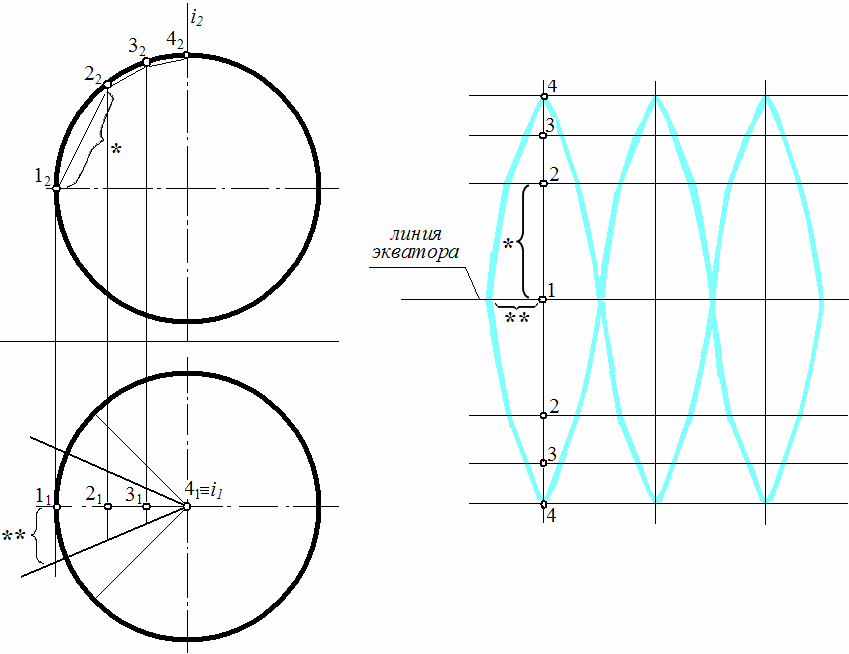• Откладываем на этой линии расстояния, взятые с фронтальной пр-ии, получим высоту доли. А вправо и влево – расстояния, взятые с гор. пр-ии.

Далее точки соединяем плавной линией с помощью лекало.

Таких долей должно быть 8.

Билет№26