1) Признак принадлежности т-ки и прямой пл-ти.

Теорема 1: Прямая  пл-ти, если она имеет с ней две общие т-ки.

Теорема 2: Т-ка  пл-ти, если она расположена на прямой, лежащей в данной пл-ти.

2) Построить т-ку пересечения прямой ℓ с пл-тью общего положения, заданного ∆ АВС. (основная позиционная задача)

Решение

Алгоритм решения задачи:

1). Выбор посредника

Q  П₂  Q_П2  ℓ

След этой пл-ти Q_П2 совпадает с ℓ₂.

2). Построение ЛП Q с заданной пл-тью ∆ АВС

Q ∩ ∑  (1₂ – 2₂)  (1₁ – 2₁) – ЛП

3). Опред. т-ки пересечения прямой с пл-тью - т. К₁  т. К₂

ℓ ∩ (1 - 2)  т. К

4). Опред. видимость прямой ℓ методом конкурирующих т-ек.

Билет17

1) Главные линии пл-ти (особые)

1.Горизонталь пл-ти – прямая, принадлежащая заданной пл-ти и || П₁

Если пл-ть задана следами, то фронт-ная пр-ия гор-ли всегда ||оси Х₁₂, а гор-ная пр-ия её - || горизонтальному следу пл-ти.

2 Фронталь пл-ти – прямая, принадлежащая заданной пл-ти и || П₂

Если пл-ть задана следами, то гор-ная пр-ия фр-ли всегда || оси Х₁₂, а фронт-ная пр-ия её - фронтальному следу пл-ти

2) развёрткой поверхности наз-ся плоская фигура, получаемая при последовательном совмещении пов-ти с пл-тью, без образования складок и разрывов

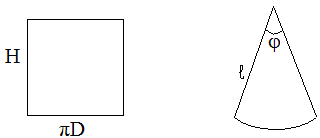
Боковая поверхность цилиндра представляет собой прямоугольник со сторонами Н, πD.

Боковая поверхность конуса представляет собой сектор круга, радиус которого равен ℓ - длине образующей конуса, а угол при его вершине  = 360⁰ R / ℓ.

Билет№18

1 )Линия наибольшего ската (ЛНС) – это прямая, - ая к горизонтали плоскости и составляющая max-ый угол с плоскостью П₁ (эта линия определяет угол наклона заданной пл-ти).

2) Развёртка пирамиды.

Мы выяснили, что для построения развёртки необходимо определить нат. величины всех элементов поверхности.

Основание пирамиды параллельно плоскости П₁, поэтому оно уже спроецировано на эту плоскость в НВ:

∆ АВС  П₁  ∆ А₁ В₁ С₁ – НВ

Необходимо найти НВ боковых граней, она состоит из треугольников. Для построения НВ треугольников, необходимо определить Н В -ны боковых ребер.

SС || П₂ (в простр-ве), S₁ C₁ || Х₁₂, т.е. S₂С₂ –НВ (на черт.).

Поэтому необх. найти НВ–ны SA и SВ вращением вокруг проецирующей оси i₁ ≡ S₁ .

После определения НВ-ин всех элементов, строим развёртку пирамиды.

Предположим на грани ВSC находится т-ка М₁, необходимо нанести ее на развёртку. Для этого через данную т-ку проводят прямую (S - 1₁), соединяющую вершину и основание пирамиды  определяем М₂  находим НВ прямой (S - 1₁) вращением вокруг оси Þ наносим на развёртку данную прямую и т-ку М.

Билет№19

1) Линия наибольшего наклона – это линия, -ая к фронтали плоскости и составляющая наибольший угол с пл-тью П₂.