2) Поверхности, образованные вращением плоской кривой.

Поверхности данной группы называются поверхностями общего положения.

Алгоритм построения поверхностей:

1. На меридиане (образующей) выделить ряд т-ек;

2. Каждую т-ку повернуть вокруг оси i до положения || оси Х₁₂, т.е провести параллели;

3. Определить проекции точек на другой плоскости проекций;

4. Полученные точки соединить плавной огибающей касательной линией для получения очерка поверхности;

5. Определить видимость поверхности.

Билет№7

1) Прямые частного положения – это прямые, параллельные или перпендикулярные какой-либо пл-ти пр-ий. Существуют 6 прямых частного положения, которые, в свою очередь, делятся на две группы:

Прямые уровня – это прямые, параллельные какой-либо плоскости пр-ий

Проецирующие прямые – это прямые, перпендикулярные какой-либо пл-ти пр-ий,

Если в пространстве прямая расположена в пл-ти пр-ий, то на черт. одна из её пр-ий совпадает с осью Х₁₂

2)Принадлежность т-ки поверхности.

Теорема: т-ка принадлежит поверхности вращения, если она лежит на параллели этой поверхности.

Поэтому, чтобы построить недостающую проекцию т-ки на поверхности вращения, необходимо провести через неё параллель и найти на другой проекции данной параллели искомую т-ку

Билет№8

1) Принадлежность т-ки линии

Теорема : Т-ка принадлежит линии, если одноимённые проекции т-ки лежат на одноимённых проекциях линии.

2) Поверхности, образованные вращением окружности.

Определитель такой поверхности: Σ ( i, ℓ ), где i - ось вращения, ℓ - окружность.

а) сфера (шар) – поверхность, образованная вращением окружности вокруг ее диаметра

б) тор – поверхность, образованная вращением окружности вокруг оси, лежащей в пл-ти окружности, но не совпадающей с её диаметром

открытый тор (кольцо) образуется в случае, если окружность не пересекает ось вращения.

закрытый тор – ось вращения лежит в пл-ти окружности, не пересекаясь, но касаясь окружности.

Билет №9

1) Взаимное расположение прямых линий.

Прямые в пространстве могут:

1. быть параллельными;(которые лежат в одной плоскости и не имеют общих точек)

2. пересекаться;(лежат в одной плоскости и имеют 1 общую точку)

3. скрещиваться.(не лежат в одной плоскости и не параллельны)

2) Поверхности, образованные вращением кривых II порядка.

При вращении кривых II порядка (эллипсы, параболы, гиперболы), образуются поверхности, называемые: эллипсоидом, параболоидом, гиперболоидом вращения.

Определитель поверхности:

Σ ( i, ℓ ), где i - ось вращения, ℓ - кривая.

а) эллипсоид вращения - образуется, если сферу сжать или растянуть вдоль одного из диаметров, его меридианом является эллипс. Если эллипс вращается вокруг большой оси, эллипсоид наз-ся вытянутым (рис.1); если вращение происходит вокруг малой оси, эллипсоид наз-ся сжатым или сфероидом

б) параболоид вращения – образуется при вращении параболы вокруг её оси.

Параболоидом вращения является поверхность параболических зеркал, применяемых в прожекторах и фарах автомобилей, где используется фокальное свойство параболы; если в фокусе параболы поместить источник света, то световые лучи, отражаясь от параболы, будут распространяться параллельно друг другу. На этом же свойстве основано и действие звукоулавливателей и радиотелескопов

в) гиперболоид вращения – образуется вращением гиперболы вокруг её оси (т.е. данная поверхность может быть образована т.ж. вращением прямой линии, что мы и рассмотрели выше)

Билет№10

1) Теорема о прямом угле.

Если одна сторона прямого угла параллельна какой-либо плоскости пр-ий, а другая сторона не перпендикулярна к ней, то на эту плоскость пр-ий прямой угол проецируется в НВ

Если две прямые пересекаются под прямым углом, то проекции их в общем случае образуют угол, не равный 90⁰.

Для того, чтобы прямой угол проецировался в НВ, необходимо и достаточно, чтобы одна из его сторон была ||-на, а другая не -на пл-ти пр-ий.

Действительно, пусть сторона АВ прямого угла АВС ||-на пл-ти П₁. требуется доказать, что проекция его: угол А₁В₁С₁ = 90⁰.

Прямая АВ -на пл-ти ∑, т.к. АВ -на двум прямым этой пл-ти ВС и ВВ₁, проходящим через т-ку В.

Прямая АВ и её пр-ия А₁В₁ – две ||-ые прямые, а потому А₁В₁ также -на пл-ти ∑. Следовательно, А₁В₁ -на В₁С₁.

2) Свойство проецирующей поверхности:

Если одна из пр-ий линии, принадлежит проецирующей поверхности, то другая проекция линии совпадает со следом этой поверхности

Билет№11

1) Пл-ти могут быть заданы следующими определителями:

1. Т ремя т-ми, не лежащими на одной прямой. (тремя несовпадающими т-ми).

∑ (А,В,С)

2. П рямой и т-кой, не лежащей на ней.

∑ (ℓ, А)

3. Двумя пересекающимися прямыми.

∑ (a ∩ b)

4. Двумя параллельными прямыми.

∑ (a || b)

5. Плоской фигурой.

∑ ( АВС)

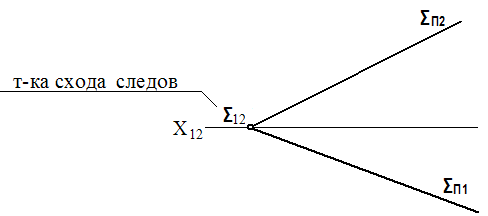
6. Следами.

∑ ( ∑_П1, ∑_П2 )

2) Свойство проецирующей поверхности:

Если одна из пр-ий линии, принадлежит проецирующей поверхности, то другая проекция линии совпадает со следом этой поверхности

Билет№12

1) Пл-ти общего положения – пл-ть ни параллельная, ни перпендикулярная ни одной из пл-тей пр-ий.