Два представления о сходимости qr-, ql-алгоритмов

Рассмотрим вопрос о сходимости 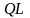-алгоритма. Если сдвиги 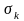не используются, то -алгоритм называется основным.

Вообще с , -алгоритмами связаны два представления о сходимости. Строго говоря, сходимость , -алгоритмов нужно понимать как сходимость матричной последовательности . В общем случае можно показать, что такая последовательность сходится к диагональной матрице, на диагонали которой находятся собственные значения исходной матрицы (симметричной). Если - несимметричная матрица, то матричная последовательность сходится к блочно-диагональной матрице, каждый диагональный блок которой отвечает собственному значению.

Однако можно понимать сходимость несколько иначе.

Теорема (случай симметричной матрицы). Пусть собственные значения матрицы удовлетворяют условию:

.

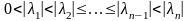Пусть матричная последовательность получена основным -алгоритмом, тогда имеет место равенство:

,

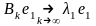где .

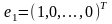В соответствии с приведенной теоремой сходимость понимается как стремление к 0 внедиагональных элементов первого столбца матрицы. На практике как только 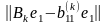становится малой, это означает, что элемент 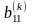можно рассматривать как приближенное значение собственного значения . После этого, если не является кратным, итерационный процесс можно продолжить для матрицы размера , отбросив первую строку и первый столбец, и т.д.

Теорема о сингулярном разложении матрицы

Пусть — -матрица с элементами , ( ). Для нее справедливо разложение, называемое сингулярным:

, (1)

где ― матрицы размерности и соответственно, , , при этом являются ортогональными , т.е. удовлетворяют соотношениям: , где ― единичная матрица соответствующей размерности. Столбцы матрицы и матрицы называют соответственно левыми и правыми сингулярными векторами (СНВ) матрицы , величины ― сингулярными числами (СНЧ), а сингулярными тройками . При рассматривается сингулярное разложение матрицы .

Разложение (1) может быть представленно в форме внешних произведений:

.

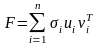В общем случае сингулярное (спектральное) разложение матрицы определяется неоднозначно. Вспомним, что вектор называется лексикографически положительным, если его первая ненулевая компонента положительна. Назовем сингулярное разложение (1) нормальным, если столбцы матрицы лексикографически положительны.

Теорема. Невырожденная матрица имеет единственное нормальное сингулярное разложение, если ее СНЧ попарно различны:

.

Утверждение 2. Пусть есть сингулярное разложение -матрицы в соответствии с (1). Собственными значениями симметричной матрицы 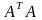являются 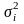, а правые СНВ 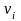— ортонормированные СВ .

Доказательство. Для матрицы имеет место соотношение:

. (2)

Равенство (2) очевидно представляет спектральное разложение матрицы , причем — ее СВ, а диагональные элементы — СЗ.