
- •1.Метод Ньютона решения нелинейного уравнения. Геометрический смысл метода Ньютона
- •Метод хорд решения нелинейного уравнения. Геометрический смысл
- •И непрерывны на ;
- •Скорость сходимости метода хорд. Преимущества и недостатки
- •Метод Ньютона решения системы нелинейных уравнений, его модификация, уменьшающая вычислительную сложность
- •Подобное преобразование матрицы, его свойства
- •Лемма Гершгорина
- •Алгоритм определения количества собственных значений, меньших заданного числа, его преимущества и недостатки
- •Алгоритм поиска ближайшего к заданному числу собственного значения
- •Степенной метод нахождения максимального по модулю собственного значения. Область применимости степенного метода
- •Метод обратной итерации нахождения минимального по модулю собственного значения. Условия целесообразности его использования
- •Нахождение наименьшего собственного значения положительно определенной матрицы
- •Преобразование отражения. Сведение матрицы к почти треугольному виду
- •Сохранение ширины ленты матрицы в qr-, ql-алгоритмах
- •Два представления о сходимости qr-, ql-алгоритмов
- •Теорема о сингулярном разложении матрицы
- •Чувствительность собственных значений (сингулярных чисел) и собственных векторов (сингулярных векторов) к возмущающим воздействиям
- •Задача наименьших квадратов. Решение линейной задачи наименьших квадратов с помощью сингулярного разложения матрицы
- •Метод решения задачи Коши, основанный на разложении решения в ряд Тейлора
- •Метод Эйлера решения задачи Коши. Геометрический смысл метода Эйлера
- •Монотонные матрицы. Достаточное условие монотонности матрицы
Метод обратной итерации нахождения минимального по модулю собственного значения. Условия целесообразности его использования
Квадратная -матрица имеет полную систему нормированных собственных векторов , определенных в (1), и предположим, что
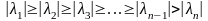 .
(6)
.
(6)
Для произвольно выбранного вектора определим:
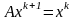 ,
(7)
,
(7)
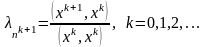 (8)
(8)
Если матрица невырожденная, то уравнение (7) можно записать в виде:
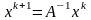 .
.
Итерации
(7), (8) в этом случае описывают степенной
метод для матрицы
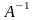 ,
обратной к
.
Если
,
обратной к
.
Если
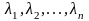
собственные значения матрицы , то
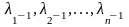
собственные
значения матрицы
,
а соответствующие собственные векторы
совпадают. Тогда согласно условию (6)
при
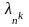 сходится к максимальному по модулю
собственному значению матрицы
,
т.е. к минимальному по модулю собственному
значению матрицы
.
Векторная последовательность
при
стремится по направлению к вектору
сходится к максимальному по модулю
собственному значению матрицы
,
т.е. к минимальному по модулю собственному
значению матрицы
.
Векторная последовательность
при
стремится по направлению к вектору
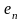 .
.
Вычисление
обратной матрицы является трудоемкой
задачей, поэтому имеет смысл вектор
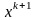 определять как решение системы линейных
алгебраических уравнений (7). Тогда метод
обратной итерации имеет смысл использовать
в виде:
определять как решение системы линейных
алгебраических уравнений (7). Тогда метод
обратной итерации имеет смысл использовать
в виде:
Шаг 1. Выбрать единичный вектор .
Шаг 2. Для сделать:
а) решить систему линейных уравнений
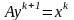 ;
;
б)
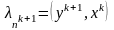 ;
;
в) ;
г)
сравнить
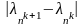 с заданной погрешностью вычисления.
с заданной погрешностью вычисления.
Алгоритм
этого метода записывается аналогично
алгоритма степенного метода. При этом
целесообразно предварительно разложить
матрицу
в произведение
,
где
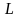 -
нижняя треугольная матрица с единицами
на главной диагонали, а
- верхняя треугольная. Если такое
разложение имеется, то количество
операций на каждом шаге метода обратной
итерации сравнимо с количеством операций
для степенного метода. При этом нужно
арифметических операций для этапа 2(а),
операций для этапа 2(б),
-
на этапе 2(в). Значительные начальные
затраты на треугольное разложение
матрицы (
-
нижняя треугольная матрица с единицами
на главной диагонали, а
- верхняя треугольная. Если такое
разложение имеется, то количество
операций на каждом шаге метода обратной
итерации сравнимо с количеством операций
для степенного метода. При этом нужно
арифметических операций для этапа 2(а),
операций для этапа 2(б),
-
на этапе 2(в). Значительные начальные
затраты на треугольное разложение
матрицы (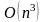 )могут
быть амортизированы по всем сделанным
шагам. Недостатки этого метода аналогичны
степенному. Но для метода обратной
итерации выбор сдвига (о чем будет
рассказано ниже) может значительно
улучшить скорость его сходимости.
)могут
быть амортизированы по всем сделанным
шагам. Недостатки этого метода аналогичны
степенному. Но для метода обратной
итерации выбор сдвига (о чем будет
рассказано ниже) может значительно
улучшить скорость его сходимости.
Нахождение наименьшего собственного значения положительно определенной матрицы
Рассмотрим еще один способ определения наименьшего собственного значения матрицы.
Пусть
- симметричная и положительно определенная
матрица. В этом случае все ее собственные
значения положительны. Обозначим
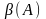 -
максимальное,
-
максимальное,
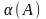 - единственное минимальное собственные
значения матрицы.
- единственное минимальное собственные
значения матрицы.
Рассмотрим
новую матрицу
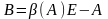 и новую задачу на собственные значения
для этой матрицы:
и новую задачу на собственные значения
для этой матрицы:
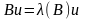 .
.
Если
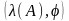 - собственная пара для
,
то
- собственная пара для
,
то
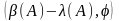 - собственная пара для
.
Действительно:
- собственная пара для
.
Действительно:
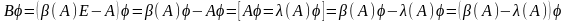 .
.
Поскольку
меньшему
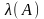 отвечает большее
отвечает большее
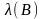 ,
то
,
то
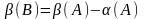 .
.
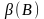 -
единственное, его можно вычислить при
помощи степенного метода, а затем
определить:
-
единственное, его можно вычислить при
помощи степенного метода, а затем
определить:
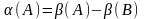 .
.
Таким образом, для вычисления нам нужны максимальные собственные значения матриц и .
