Подобное преобразование матрицы, его свойства

Определение 4. Пусть 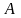- данная матрица, - невырожденная матрица. Тогда преобразование

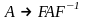
называется подобным преобразованием матрицы .

Подобное преобразование играет огромную роль в процессе решения задач на собственные значения в силу следующего свойства.

Теорема. Пусть матрица 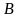получена путем подобного преобразования матрицы , т.е. . Если - собственная пара матрицы , то - собственная пара . Иными словами: подобное преобразование не меняет спектр матрицы.

Доказательство. Рассмотрим характеристический многочлен для матрицы :

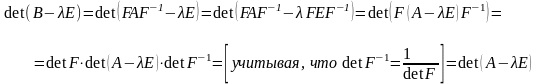
т.е. характеристические многочлены матриц и совпадают, а значит совпадают характеристические уравнения, а следовательно, совпадают и спектры: собственные значения у матриц и одинаковые.

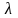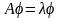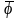Пусть теперь - собственный вектор матрицы , отвечающий собственному значению . Это означает, что . По доказаному выше - это собственное значение и матрицы , а значит существует собственный вектор матрицы , отвечающий , т.е. такой, что: .

.

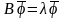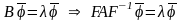Умножим обе части последнего равенства на матрицу слева. Получим:

,

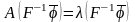т.е. вектор - собственный вектор матрицы . Зная, что - собственный вектор матрицы , а значит, и для любого 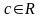, получаем, что

,

откуда после умножения обеих частей на матрицу слева получаем:

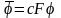
собственный вектор матрицы . При 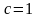получаем: , что и требовалось доказать.

Лемма Гершгорина

Определение 1. Локализация собственных значений - определение границ спектра, или границдля каждого собственного значения.

Лемма Гершгорина. Пусть - произвольная матрица. Обозначим

.

Все собственные значения матрицы находятся в объединении 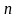кругов с центрами в точках и радиусами 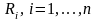, называемых кругами Гершгорина, т.е. для каждого собственного значения матрицы обязательно найдется круг, что:

.

Доказательство. Покажем, что каждое собственное значение матрицы попадает хотя бы в один из кругов Гершгорина. Пусть - собственное значение матрицы , а - соответствующий собственный вектор, т.е.

. (1)

Обозначим через 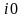индекс такой компоненты вектора , что

.

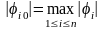Индекс может определяться неоднозначно.

Запишем уравнение с номером из системы (1):

. (2)

В левой части равенства (2) выделим слагаемое с номером :

.

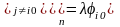Преобразуем эквивалентным образом последнее равенство:

,

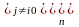Учитывая, что , а собственный вектор не может быть нулевым, то 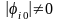, , 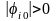поэтому последнее неравенство можно разделить почленно на 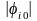, не меняя знак:

. (3)

Поскольку , то 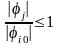, тогда (3) можно продолжить:

,

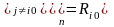что и требовалось доказать.

Следствие. Если все круги Гершгорина, отвечающие матрице попарно не пересекаются, то каждый из них содержит точно одно собственное значение.