Билет 5. Выбор вида эмпирической зависимости
Нами была рассмотрена линейная зависимость вида у=Ах+В для случаев, когда А 0; В = 0 и А 0, В 0. Но, к сожалению, построение этой зависимости не дает ответа на вопрос о том, какая аналитическая зависимость наилучшим образом подходит к имеющемуся распределению. Наиболее популярные на практике эмпирические зависимости имеют вид:
1) линейная функция: у = Ах + В;
2) показательная функция: у = АВх ;
3) дробно-рациональная функция: у = (Ах+В)-1;
4) логарифмическая функция: у = А . ln(х)+В;
5) смешанная функция: у = АхВ.
В зависимости от параметра В она определяет параболическую (В > 0), гиперболическую (В < 0) и линейную (В = 0) зависимости;
6) гиперболическая функция: у = А + В/х;
7) дробно-рациональная функция: у=х/(Ах+В).
Билет 6. Определение параметров эмпирической зависимости
Часто из физических соображений следует, что зависимость между величинами хорошо описывается моделью вида , где вид зависимости известен. Тогда применение критерия наименьших квадратов приводит к задаче определения искомых параметров из условия минимума функции:
Если зависимость от параметров нелинейна, то экстремум функции ищут методами минимизации функций нескольких переменных.
Билет 7. Решение системы алгебраических уравнений при помощи функции lsolve.
Системы уравнений многие просто-таки ненавидят еще со школы — прямо как русскую литературу. Что ж, школа может привить отвращение ко многим вещам, которые без нее могли бы оказаться гораздо более интересными. Как и любая обязаловка, она убивает романтику изучения чего-то нового. Но теперь, когда вас никто не заставляет изучать решение систем уравнений, вы можете взглянуть на них с совершенно новой для себя стороны. И поможет в этом, конечно же, MathCAD.
Для обозначения систем линейных алгебраических уравнений у математиков есть своя аббревиатура — СЛАУ. Ее используют намного чаще, чем полное название, что, в общем-то, вполне естественно — эта аббревиатура и произносима легко, и не перекрывается с другими математическими аббревиатурами. Так что и мы с вами тоже будем ее применять. СЛАУ называется система уравнений следующего вида:
k11x1 + k12x2 + … + k1nxn + l1 = 0
k12x1 + k22x2 + … + k2nxn + l2 = 0
…
kn1x1 + kn2x2 + … + knnxn + ln = 0
Здесь kij и li — какие-то числовые константы, называемые, соответственно, коэффициентами и свободными членами уравнений, а xj — переменные. Такие уравнения обычно записывают также с помощью матриц:
KX + L = 0
С помощью функции lsolve можно получать и аналитические решения СЛАУ. Давайте попробуем заменить одно из чисел в матрице коэффициентов на букву — например, "а". Функция lsolve сразу выдаст ошибку, но не нужно этого пугаться — нужно просто заменить знак равенства на стрелку (ее можно найти на панели инструментов Symbolic или же записать комбинацией клавиш Ctrl + .). Дело в том, что знак "равно" в MathCAD'е используется для численных вычислений, а стрелка — для символьных, то есть при решении систем уравнений в общем виде нужно применять именно стрелку.
Билет 8. Решение системы алгебраических уравнений матричным методом.
AX = B,
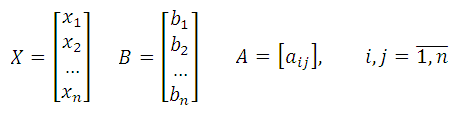
В скалярной форме записи
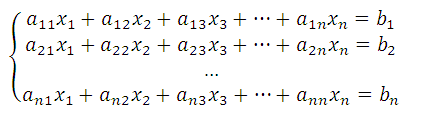
Система (1) имеет
единственное решение, если
Билет 9. Решение системы алгебраических уравнений Метод Крамера.
Метод Крамера применяется для решения систем линейных алгебраических уравнений (СЛАУ), в которых число неизвестных переменных равно числу уравнений и определитель основной матрицы отличен от нуля. В этой статье мы разберем как по методу Крамера находятся неизвестные переменные и получим формулы. После этого перейдем к примерам и подробно опишем решение систем линейных алгебраических уравнений методом Крамера.
Метод Крамера основывается на двух свойствах определителя матрицы:
Определитель квадратной матрицы
Сумма произведений элементов какой-либо строки (столбца) квадратной матрицы на алгебраические дополнения соответствующих элементов другой строки (столбца) равна нулю
Билет 10. Критерия адекватности в виде минимума суммы квадратов отклонений между экспериментальными и расчетными значениями.
В качестве внутренних критериев могут фигурировать списки факторов, задействованных в моделях (Брусиловский, Розенберг, 1981). Так, если FX - список факторов, с помощью которых задается динамика некоторой экосистемы в имитационной модели, а FY - список факторов, использованных в самоорганизующейся модели той же экосистемы, то возможны четыре ситуации.
Ситуация 1. FX Ì FY, т.е. в имитационной модели отсутствуют некоторые существенные факторы. Здесь и далее под существенными понимаются факторы, включенные ЭВМ (без субъективного выбора исcледователем) в оптимальную по сложности самоорганизующуюся модель, построенную по результатам натурных наблюдений над экосистемой. Таким образом, имитационная модель считается недоусложненной и признается внутренне неадекватной.
Ситуация 2. FX É FY, т.е. в имитационной модели присутствуют "лишние" факторы (несущественные по результатам самоорганизации). Имитационная модель считается переусложненной, но может быть признана внутренне адекватной.
Ситуация 3. FX U FY = Æ , т.е. в имитационной модели одновременно отсутствует часть существенных факторов и присутствует часть несущественных факторов. В этом случае имитационная модель одновременно является недо- и переусложненной по сравнению с соответствующей самоорганизующейся моделью и также должна быть признана внутренне неадекватной.
Ситуация 4. FX = FY, т.е. списки факторов, характеризующих состояние экосистемы в имитационной и самоорганизующейся моделях, совпадают (фактически этой ситуации соответствует рассмотренный выше вариант сравнения аналитических моделей взаимодействия популяций растений). Имитационная модель должна быть признана внутренне адекватной.
Билет 11. Интегральный критерия адекватности.
Билет 12. Классификация языков программирования
Существующие языки программирования классифицируют по четырём основным группам: процедурные, объектно ориентированные, функциональные и логические. Кратко рассмотрим особенности каждого подхода.
Процедурное программирование
Программа отделяется от данных. Программа состоит из последовательности команд, обрабатывающих данные. Данные как правило хранятся в виде переменных. Весь процесс вычисления сводится к изменению их содержимого.
Декларативные языки программирования
К ним относятся функциональные и логические языки программирования. В этих языках не производится алгоритмического действия явно, то есть алгоритм не задается прграммистом, а строится самой программой. В декларативных языках задается, производится построение какой-либо структуры или системы, то есть декларируются (объявляются) какие-то свойства создаваемого объекта. Эти языки получили широкое применение в системах автоматизированного проектирования (САПР), в так называемых CAD-пакетах, в моделировнии, системах исккусственного интеллекта
Объектно-ориентированное программирование
Переменные и функции группируются в так называемые классы. Благодаря этому достигается более высокий уровень структуризации программы. Объекты, порождённые от классов вызывают методы (функции или процедуры) друг друга и меняют таким образом состояние свойств (переменных). В принципе объектно ориентированный способ написания программ не является чем то особенным и самостоятельным, поскольку базируется на процедурной модели программирования.
Языки программирования для компьютерных сетей
Сетевые языки предназначены для организации взаимодействия удаленных компьютеров в интенсивном интерактивном режиме, а поэтому они построены на принципах интерпретации, то есть построчной, интерактивной обработки строк программного кода, описывающего некоторый сценарий (скрипт) сетевого взаимодействия компьютеров, поэтому часто они называются скриптовыми языками.