Тема IV. Чисельне інтегрування

§1. Інтерполяційні формули чисельного інтегрування

Якщо функція неперервна на відрізку й відома її первісна , то визначений інтеграл можна обчислити за формулою Ньютона-Лейбніца:

.

Проте на практиці часто цією формулою неможливо скористатися з двох причин:

1. первісна не виражається в елементарних функціях;

2. функція задана у вигляді таблиці.

У цих випадках застосовують методи числового інтегрування. Ці методи полягають у тому, що функцію замінюють на відрізку апроксимуючою функцією простішого вигляду (наприклад, многочленом), а потім приймають .

Розглядатимемо методи обчислення визначених інтегралів без особливостей, тобто інтегралів зі скінченими границями інтегрування від функцій, які на проміжку інтегрування не перетворюються на нескінченність.

Розглянемо визначений інтеграл

, (1)

де – підінтегральна функція, – задана вагова функція така, що .

Однією із загальних ідей при побудові алгоритмів наближеного обчислення інтегралу (1) є така: для функцій будується деяке наближення і наближено покладають

, (2)

тут наближення має бути таким, щоб інтеграл (2) обчислювався простіше, ніж (1).

На практиці поширені наближення , які лінійно виражаються через значення функції та її похідних у точках сітки .

Тоді, в загальному, формула для має вигляд:

(3)

і називається квадратурною формулою. Числа називаються вузлами квадратурної формули, а числа – коефіцієнтами або ваговими коефіцієнтами. Величина

(4)

називається залишковим членом квадратурної формули. На практиці найчастіше вживають квадратурні формули виду:

, (5)

у яких використовуються лише значення функції і не використовуються похідні. Формулу (5) можна отримати, якщо вибрати у вигляді:

(6)

де – інтерполяційний многочлен степеня для функції за вузлами фундаментальні інтерполяційні многочлени

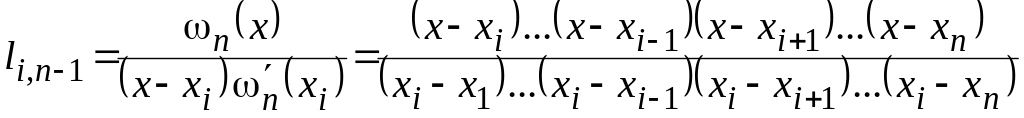(7)

Тоді,

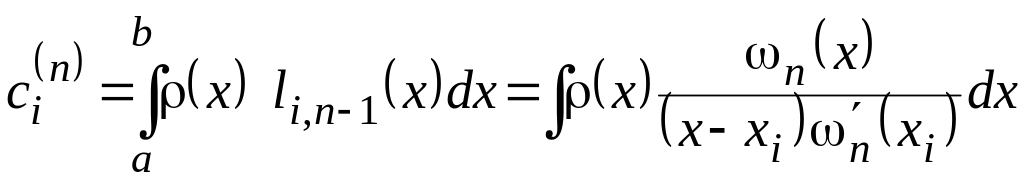(8)

і формула (5) називається формулою інтерполяційного типу.

Якщо залишковий член квадратурної формули дорівнює нулю на множині всіх алгебраїчних многочленів не вище – го степеня, то кажуть, що квадратурна формула має алгебраїчний ступінь точності .

Тоді, алгебраїчний степінь точності формули інтерполяційного типу (5) з ваговими коефіцієнтами (8) є , бо

.

Найпростішими серед формул інтерполяційного типу, які широко використовуються в практичних обчисленнях є формули Ньютона-Котеса.

§2. Квадратурні формули складеного типу

Якщо у квадратурній формулі (5) з ваговими коефіцієнтами (8) для інтеграла (1) з вагою вузли рівновіддалені, то така формула називається формулою Ньютона-Котеса. Якщо крок , , тобто множина вузлів не містить точок і , то квадратурна формула Ньютона-Котеса називається формулою вікритого типу. Якщо ж , , тобто множина вузлів містить точки і , токвадратурна формула Ньютона-Котеса називається формулою замкненого типу.

Якщо покласти , то для формул відкритого типу , а для формул замкненого типу .Тоді і виконаємо у інтегралі заміну та позначимо , то

. (1)

У інтегралі (1) замінимо функцію інтерполяційним многочленом Лагранжа з вузлами у точках , тобто

. (2)

Підставивши вираз (2) у інтеграл (1) дістанемо

,

де

, (3)

, (4)

Враховуючи заміни, перепишемо (3) у вигляді

, (5)

де

.

Порівнюючи (6) і (5) § 4, отримаємо, що тут

.

Значення не залежить від проміжку інтегрування і можуть бути обчислені 1 раз і назавжди. При цьому справджується рівність , яка означає рівність рівновіддалених від кінців проміжку інтегрування коефіцієнтів і приблизно двічі скорочує кількість обчислень.

Величини при зростанні необмежено зростають . А це означає, що при великих малі похибки в значеннях функції можуть дати велику похибку у квадратурній сумі – неусувна похибка. Тому на практиці не використовують формули Ньютона- Котеса з великим , а щоб зменшити похибку при чисельному інтегруванні на великому проміжку , то його попередньо розбивають на велику кількість малих інтервалів і на кожному з них застосовують квадратурну формулу з невеликою кількістю вузлів. Знайдена таким чином квадратурна формула називається формулою складеного типу.