§2. Метод ділення навпіл

Найпростішим методом розв’язування рівняння є метод ділення навпіл, який ще називають методом дихотомії або бісекції. Цей метод дає змогу також довести існування кореня на відрізку , якщо , тобто непервна функція на кінцях відрізка набуває значення різних знаків або перетворюється в 0.

Обчислення виконують за такою схемою.

Ділимо відрізок пополам і замінюємо його тією половиною, яка містить корінь:

якщо , то ;

якщо , то

При (або ) обчислення припиняються, тому, що середина останнього відрізка дає значення кореня із заданою точністю , а саме, .

Такий ітераційний процес збігається із швидкістю геометричної прогресії із знаменником , тобто

Кількість ітерації, потрібних для виконання нерівності

є

Основний недолік методу – повільна збіжність.

§ 3. Метод Ньютона

Нехай рівняння на відрізку має ізольований корінь , тобто , а функції і неперервні та зберігають знак на відрізку .

Якщо у розвиненні рівняння в околі точки

,

де , , – точне значення кореня, відкинути останній доданок і замінити на , то отримаємо рівняння вигляду

.

Розв’язавши його відносно , дістанемо

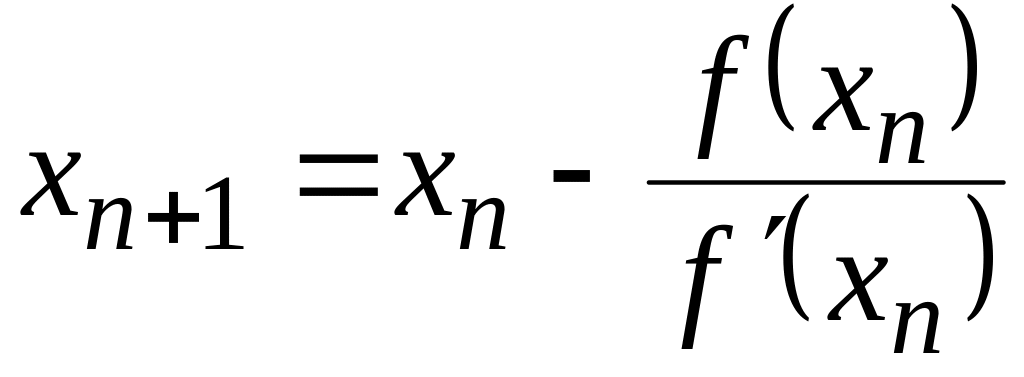, , . (4.1)

Формула (4.1) визначає метод Ньютона, який ще називають методом лінеаризації або методом дотичних. Як бачимо метод Ньютона є методом простої ітерації , де функція

. (4.2)

Припустимо, що відрізок містить єдиний корінь рівняння і функція має неперервні похідні , які не перетворюються в нуль на . Тоді , причому .

Це означає, що існує окіл точки , в якому , і якщо початкове наближення взято з цього околу, то за теоремою §3 послідовність , знайдена за методом Ньютона, буде збігатися до .

Теорема.

Нехай функції неперервні і відмінні від нуля на (зберігають знак на ), тоді якщо початкове наближення задовольняє умові то послідовність методу Ньютона збігається до кореня .

Для оцінки похибки припустимо, що

.

Тоді за теоремою Лагранжа отримаємо

або врахувавши, що –

(4.3)

З іншої сторони, за формулою Тейлора

,

,

звідки будемо мати

(4.4)

Враховуючи (4.4), із (4.3) отримаємо

(4.5)

З цієї оцінки видно, що для досягнення заданої точності ітераційний процес треба продовжувати доти, поки для двох послідовних наближень не виконуватиметься нерівність .

Оцінка (4.5) є апостеріорною, а тому зручною для застосування і свідчить про високу швидкість збіжності методу Ньютона. З формули (4.2) видно, що чим більше значення в околі кореня, тим менша поправка додається до попереднього наближення. Тому, метод Ньютона зручно застосовувати тоді, коли в околі кореня графік функції має значну крутість. Недоліком методу є складність вибору початкового наближення.

Тема іi. Методи розв’язування систем рівнянь

§1. Розв’язування слар

Знаходження коренів систем лінійних алгебраїчних рівнянь (СЛАР) – одна з математичних задач, яка часто зустрічається як в інженерній, так і в науковій практиці.

Розглянемо СЛАР вигляду , де А – квадратна матриця розмірності , b – заданий вектор, х – шуканий вектор. Система у розгорнутій (покомпонентній) формі має вигляд:

З лінійної алгебри відомо, що за умови , ця система має єдиний розв’язок, який можна знайти за правилом Крамера, проте застосування цього правила для розв’язування цієї системи є надзвичайно трудомістким.

Коренем або розв’язком системи лінійних алгебраїчних рівняння називається вектор , який, будучи підставлений в систему, перетворює всі рівняння цієї системи в правильні числові рівності

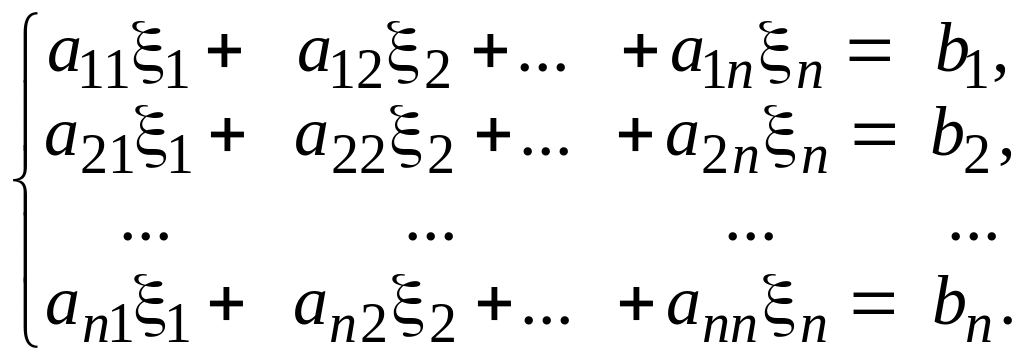
Методи розв’язування СЛАР можна поділити на дві групи: точні й ітераційні.

Точними називаються такі методи, які дають змогу знайти точний розв’язок СЛАР за допомогою виконання скінченої кількості арифметичних операцій у припущенні, що всі обчислення виконуються точно (без заокруглень), а коефіцієнти системи і вільні члени – точні числа. Але на практиці всі обчислення виконуються з обмеженою кількістю десяткових розрядів, а ірраціональні коефіцієнти і вільні члени, якщо такі є, замінюються раціональними числами. Тому в процесі обчислень вдаються до округлень, а це означає, що розв’язки, які обчислюються за точними методами, фактично є наближеними числами з певними похибками (похибками округлень). До точних методів належать правило Крамера, метод Гаусса, метод квадратних коренів, метод прогонки тощо.

Ітераційними називають такі методи, які дають змогу знайти наближений розв’язок С,ЛАР із заздалегідь указаною точністю шляхом виконання скінченої кількості арифметичних операцій, хоч самі обчислення можуть проводитися і без округлень, а коефіцієнти системи і вільні члени бути точними числами. Точний розв’язок СЛАР за допомогою ітераційних методів можна знайти лише теоретично як границю збіжного нескінченного процесу. Розв’язуючи СЛАР ітераційними методами, крім похибок округлення, потрібно враховувати також похибку методу. До ітераційних належать метод ітерації, метод Якобі, метод Зейделя тощо.

Вираз називається нев’язкою, і завжди може бути обчисленим. Нев’язка дає нам порядок точності знаходження коренів СЛАР.