Висновки

У роботі розглянуто фізичну сутність поняття гравітаційного потенціалу, історія його виникнення способи визначення та порівняння.

У результаті теоретичних досліджень, що грунтуються на дослідах коливань математичних маятників, зроблено оцінку маси та розмірів запасів залізної руди в районі міста Комсомольска. Користуючись даними отриманими за допомогою радіолокаційних вимірювань з космічних кораблів оцінено розміри неоднорідності на дні океану

Зроблено оцінку поправки до гравітаційного потенціалу згідно теорії Енштейна. Визначено енергію рознесеня частинок маси Землі на нескінченність.

Аналіз даних отриманих під час розрахунку маси та розмірів залізної руди свідчать про високу коректність провелених досліджень так як вони з високою точністью співпадають з даними отриманими з геологічної служби ПГЗКа.

Дані роботи були використані в учбовому процесі навчальних закладів міста Комсомольск (гірничного ліцею, політехнічного технікуму, школах).

На даний момент часу на Полтавському гірничо збагачувальному комбінаті видобуто 1 млрд. гірських порід. Маса розвіданої залізної руди з допомогою різних способів достатньо точно узгоджується з отриманими даними в роботі. На результат дослідження впливає нерівномірний розподіл неоднорідностей в районі міста(кар’єр та відвали). Автором роботи проведено лекції по матеріалам свого дослідження в школах міста та на виробництві.

Список використаних джерел

1. А.Ю. Дриженко и др. Открытая разработка железных руд Украины: состояния и пути совершенствования. Монография. Полтава «Полтавський літератор» 2009

2. Журнал «Успехи физических наук» том 158 выпуск 3 июль 1989 ст. №513, 514 , 515, 525,526,528, 520

3. Журнал «Квант» № 8,11

4. Задачи по физике. Под редакцией О.Я. Савченко Москва. «Наука» 1988

5. І.М. Кучерук, І.Т. Горбачук Загальний курс фізики том 3 Київ «Техніка» 1999

6. І.М. Кучерук, І.Т. Горбачук Загальний курс фізики том 1 Київ «Техніка» 1999

7. Корявов В.П. Методы решения задач в обшем курсе физики . Механика: Учеб. Пособие/В.П. Корявов, - М.: Высш. шк.,2007.-375 с.: ил.

8. Киттель Ч; Найт В.; Рудерман М. Механика: учебное руководство том 1 –М.: «Наука» 1983

9. Марио Льоцци История физики пер. с ит. издательство «Мир» Москва 1970р.

10. Мин Чен. Задачи по физике с решениями. Пер. с англ. и здательство «Мир» Москва 1978р.

11. Соколович Ю.А.; Богданова А.С. Справочное руководство по курсу физики средней школи с примерами решения задач.- Харьков : Ранок, 1999

12. Сивухин Д.В. Обший курс физики том 1 Механика издательство «Наука» Москва 1974

13. Фізика: підручник для 10 кл. загальноосвіт. навч. закл.(профільн. Рівень) авт.: Т.М. Засєкена, М.В. Головко,.-К.: Педагогічна думка, 2010.-304с.,іл.,табл.

14. Я.Б.Зельдович. Теоретическая физика. Сборник задач с решениями / Дж. Корнин, Д. Гринберг, В. Телегди. – М.:КомКнига, 2005

15. Ю.К. Гулак, Є.В. Сандакова. Фізика космосу. Видавнитство «Радянська Школа» Київ – 1976.

16. Г.И. Шипов Теория физического вакуума. Москва «НАУКА» 1997.

17. Дж. Кронин, Д.Гринберг, В. Телегди. Теоретическая Физика. Перевод с анг. Г.В. Даниляна. Под редакцией П.А. Крупчицкого. Москва.

18. Б.С. Беликов. Рещение Задач по физике. Общие методы. Москва «Высшая школа» 1986.

19. В.П Корявов. Методы решения задач в общем курсе физики. Механика. Москва «высшая школа» 2007.

20. Кл.Э. Суорц. Необыкновенная физика обыкновенных явлений. Москва «Наука» Главная редакция физико-математической литературы 1986.

ДОДАТКИ

Додаток А

ПГЗК

Підприємство, Місцезнаходження, Тип залізних кварцитів	Середній вміст заліза	Балансові запаси по категоріям, млн. тн.
		А+B+
Горишене-плавнинське	32,4	1626,0	52,0
-Магнетитове	35,1	902,3	52,0
-Кумингтонито-магнетитове	29,1	723,7	-
Лавриковське	34,8	299,3	66,7
-Магнетитове	35,2	276,6	-
-Кумингтонито-магнетитове	29,1	22,7	66,7
Резервні,розвідані
Еристовське	33,7	822,1	49,9
-Магнетитове	34,4	747,6	7,3
-Кумингтонито-магнетитове	26,7	74,5	42,6
Білановське	31,1	1626,8	37,3
-Магнетитове	33,2	1079,3	25,6
-Кумингтонито-магнетитове	27,0	546,4	11,6

Додаток Б

Кременчуцький залізо рудний район. Росташований на лівому березі р.Дніпро (Полтавська обл.). В більшості випадках він з’єднується з Кривим рогом та розглядається як одна Криворізько-Кременчуцька залізорудна зона. Район представляє полосу метаморфозо ванних залізисто-кременистих порід, які тягнуться в північно-східному направлені на 45 км. при ширині від 0,2 до 3,5км. Кременчуцьку синкліналь складають чотири родовища Криворізької серії. Найбільш продуктивним родовищем є Саксаганське потужністю до 1300м, складається із п’яти шарів залізистих кварцитів, розділених сланцевими горизонтами. Найбільш рудоносним є друге знизу під родовище потужністю 40-200м.

В районі п’ять родовищ: Горищеплавниньске, Лавриковське, Ерестовське, Білановське, та Кременчуцьке з загальними запасами більш ніж 4504млн. тон. Перші два роробляються кар’єром Полтавського ГОКа, інші три є резервними. Запаси представлені залізистим кумінгтоніто-магнетитовими кварцами (1301,9 млн.т) з середнім вмістом заліза 27,4%, магнетитовим кварцом (2033,9млн. т.) з середнім вмістом заліза 32,8% та багатими залізними рудами (28, млн.т.) з середнім вмістом заліза 58,5%

Додаток В

Робота сил поля тяжіння.

Потенціальна енергія взаємодії мас. Потенціал.

Сила тяжіння , переміщаючи тіло виконує роботу. Знайдемо роботу сили тяжіння під час руху матеріальної точки масою m у полы тяжіння, створеному точковою масою M. При елементарному переміщенні маси m, сила тяжіння виконує елементарну роботу.

=

Рис1.9 Пояснення до додатку В

де F= - модуль сили тяжіння; dR= cos a – зменшення відстані між масами m і M при переміщенні .

Робота сили тяжіння при скінченному переміщенні маси по довільній траєкторії з точки 1 у точку 2, відстані яких до маси M дорівнюють визначаються інтегралом

A=

Звідси випливає, що робота сили тяжіння не залежить від форми шляху, а визначається тільки початковим і кінцевим положенням маси m у полі тяжіння. Отже, сили тяжіння консервативні. Якщо , то маса m віддаляється від маси M як джерела поля тяжіння і A ; цю роботу виконують зовнішні сили проти сил поля тяжіння. Якщо то маса m наближається до джерела поля тяжіння і А , тобто сили тяжіння виконують додатню роботу. Оскільки сили тяжіння консервативні , то виконана ними робота при переміщенні матеріальної точки масою m між двома положеннями 1 і 2 в полі тяжіння дорівнює зменшенню потенціальної енергії маси m:

З попередніх формул дістаємо:

У задачах механіки, як уже зазначалося, основну роль відіграє не потенціальна енергія а її змінна. Тому потенціальну енергію можна відрахувати від будь-якого початкового рівня. За початок відліку потенціальної енергії можна вибрати таке розміщення тіл при якому гравітаційної взаємодії немає. Це матиме зміст коли тіла m і M перебуватимуть на нескінченній відстані ( . Тоді 1/ 0 і 0. При переміщенні матеріальної точки m з нескінченності на відстань R від тіла масою M потенціальна енергія точки m буде

U= .

При такому (умовному) виборі початкової точки відліку потенціальна енергія двох матеріальних точок, що взаємодіють, завжди від’ємна і зростає при збільшенні відстані між ними.

Для однорідного поля за нульовий рівень потенціальної енергії беруть поверхню тіла, яке створює поле. Тоді потенціальну енергію тіл, що знаходяться на відстані h від джерела поля, запишемо як

U=mGh; G-const.

Ці формули виражають потенціальну енергію взаємодії обох тіл. Якщо поле тяжіння, створене системою матеріальних точок, маси яких 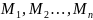, то потенціальну енергію матеріальної точки масою m, яка заходиться ввідповідно на відстанях від матеріальних точок, виражають так:

З виразу U= видно , що величина

Не залежить від маси m, а залежить тільки від маси M і відстані від цього тіла до точки поля. Ця величина скалярна, її називають потенціалом поля тяжіння. Потенціал поля є його енергетичною характеристикою. Користуючись поняттям потенціалу, формулу

можна подати так:

=m( ,

Де і - потенціали точок 1 і 2.

Потенціал точки поля тяжіння, створеного системою матеріальних точок, відповідно визначається

Оскільки поле тяжіння є потенціальним силовим полем, то між обома його характеристиками – напруженістю і потенціалом (R) існує зв'язок. Силу тяжіння, яка діє на матеріальну точку масою m, можна визначити за формулою

=m (R),

де - радіус вектор матеріальної точки проведений від точкової маси m в даній точці поля

U(R)= m (R),

Де R – відстань до центра тяжіння. При нескінченно малому переміщенні маси m сила тяжіння виконує роботу за рахунок зменшення потенціальної енергії.

Звідси знаходимо

або в координатній формі

.

Напруженість у даній точці поля тяжіння дорівнює градієнту потенціалу в цій точці, взятому із знаком мінус. Вектор grad завжди направлений у бік зменшення напружності потенціального поля і чисельно дорівнює зміні напруженості на одиниці довжини у цьому напрямі.