2.6 Знаходження поправочного коефіцієнта до гравітаційного потенціалу в теорії Ейнштейна

Згідно ньютонівській теорії тяжіння гравітаційний потенціал визначається формулою:

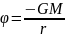
Згідно теорії Ейнштейна ця формула потребує уточнення. Якщо ввести поправку першого порядку, то гравітаційний потенціал можна записати у вигляді:

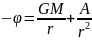
Виходячи з міркувань розмірностей попробуємо знайти вираз для поправочного коефіцієнта А. Очевидно що він повинен залежати від швидкості світла та постійних G і M. Хорошим вважається тільки рішення отримане з точністю до множника 2

Нехай D(A) – розмірність параметра А

D(A)=D(GMr)

D( )=D(m )=D (енергія)

D(r)= D( ) A ~ .

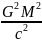Зробимо оцінку величини поправки по відношенню до ньютонівського потенціалу наприклад для Сонця:

=

Для Землі ця величина дуже мала, для Меркурія дуже вагома.

РОЗДІЛ 3 Застосування гравітаційного потенціалу в області практичних досліджень.

3.1 Визначення неоднорідності земної поверхні на дні океану.

За допомогою спеціального радіолокаційного висотоміра який знаходився на американському космічному кораблі було визначено, що поверхня океану в районі «Бермудського трикутника» нижча нормального рівня на 25 метрів. Припускаючи, що цей прогин можна пояснити присутністю під водою кульової неоднорідності, яка заповнена водою. Оцінимо радіус даної неоднорідності вважаючи, що середня глибина океану в даному районі становить h=6 км, середня густина земної породи

Вільна поверхня води в полі земного тяжіння завжди встановлюється так, що в будь якій точці її поверхні сила тяжіння перпендикулярна до неї, а отже направлена до центру Землі по радіусу. Із-за наявності кульової неоднорідності поверхня океану викривлена – сумарна сила тяжіння (зі сторони Землі і зі сторони неоднорідності) направлена, власне кажучи, не вздовж радіуса Землі.

Сила, яка діє на пробну масу m:

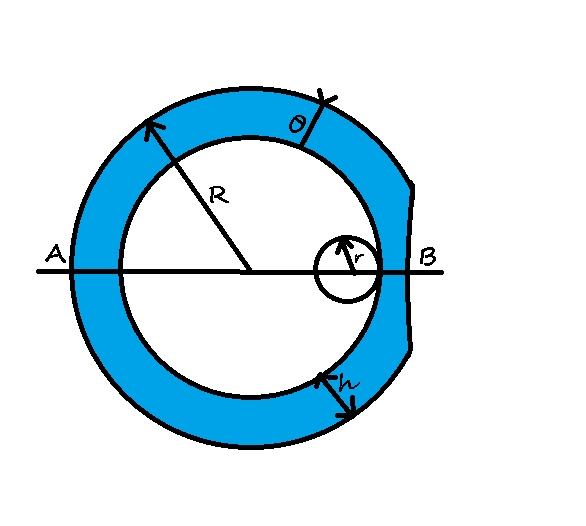
Рис Прогин в океані в районі Бермудського трикутника.

Введемо поняття потенціалу поля тяжіння точкової маси М (дорівнює потенціальній енергії одиничної маси в полі маси M). Вираження аналогічне вираженню потенціалу електричного поля точкового заряду Q:

.

(Знак мінус виражає основну відмінність між і 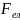: під дією гравітаційних сил тіла завжди притягуються. Оскільки потенціальна енергія при безкінечно великій відстані r прямує до нуля то в випадку сил тяжіння потенціальна енергія виявляється від’ємною.)

Потенціальна енергія частинки маси m на поверхні води повинна бути скрізь однакова(Оскільки сила тяжіння скрізь перпендикулярна поверхні , робота сили тяжіння при переміщенню частинки по поверхні дорівнює нулю.) Отже поверхня океану (поверхня землі) – еквіпотенціальна. Запишемо потенціал поля тяжіння Землі в точці А, яка знаходиться далеко від неоднорідності, і в точці В яка знаходиться безпосередньо під неоднорідністю в точці А; наявністю неоднорідності можна знехтувати вважаючи потенціал рівним , Де R- радіус Землі, M=4/3 - її маса. Щоб знайти потенціал в точці В, використаємо принцип суперпозиції. Рисунок показує суперпозицію полів тяжіння Землі та неоднорідності. З малюнка зрозуміло, що потенціал в точці В складається із потенціалу поля тяжіння Землі (без неоднорідності) та поля тяжіння кульової маси з густиною 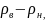тобто точкової маси ( ,

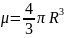де r-радіус неоднорідності, .

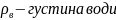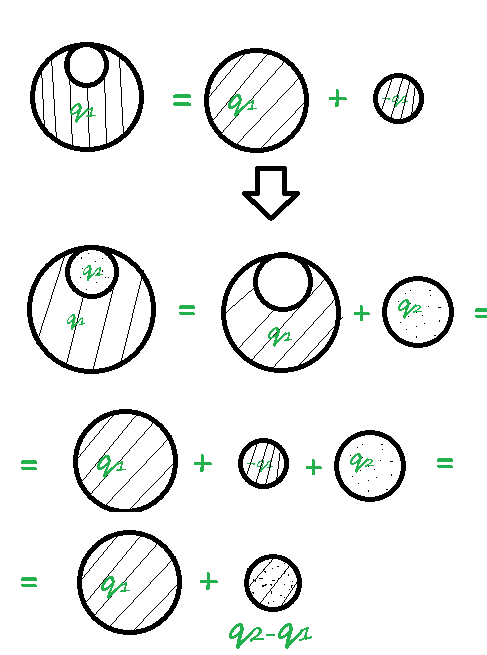
Рис Пояснення до задачі

Оскільки поверхня океану – еквіпотенціальна, 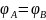, тобто

Пертворимо цей вираз:

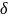Нехтуючи в лівій частині і – в правій, отримуємо .

Або підставляючи

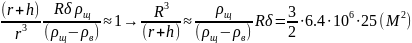
(Тут підставлені числові значення R=6.4 м,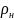 = , , 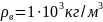Оцінимо значення . Для цього використаємо той факт, що функція монотонно зростає при . Безпосередніми розрахунками легко переконатися, що знаходиться в інтервалі між 18 та 20 км.