5.9 Определение параметров системы контроля
При двух результатах контроля (Да и Нет) возможны четыре альтернативные события, оцениваемые через их вероятности (рисунок 5.2):
Г- годное изделие признано годным, a - негодное изделие, но признано годным,
Бр- негодное изделие признано негодным, b- годное изделие, признано негодным.
Суммарная вероятность событий р(Г) + р(a) + р(b) + р(Бр) = 1,
a - ошибки первого рода; a= Nош / Nn , где Nn - общее число устройств, Nош – число устройств с дефектом, но признанных годными;
b - ошибки второго рода; они дают относительно небольшие потери.
Проведём анализ функции стоимостных потерь от ошибок первого рода. Необходимо добиться, чтобы a® min, т.е. Спотери = F (a) ® min; но затраты на контроль существенно увеличиваются: при a ® 0 имеем lim g(a) ®¥ .
Пример 5.5. Решим задачу поиска оптимальных параметров системы контроля. Последовательность решения:
1. Введем целевую функцию j(a):
j(a) = F(a) + g(a), где F(a) - потери от ошибок (функция потерь),
g(a)
- затраты на контроль.
0
Рисунок 5.3 – Влияние ошибок первого рода
2. Функция потерь F(a) = Сошиб ×Nош = Сошиб ×a Nn .
3. Потери второго типа определяются по формуле: g(a) = А×е – к .
Следовательно, j(a) = Сошиб ×a Nn + А×е– к Þ min, поэтому в точке минимума производная по a равна нулю. Продифференцируем :
j/(a) = Сошиб × Nn – к А×е– к .
После логарифмирования получим: a* = (1/к)×ln [(Сошиб × Nn) / (к×A)].
4. Допустим, путем статистического анализа максимальные затраты соответствуют минимуму ошибок: к=10, Сошиб = 2000, Nn=100000, А=3000. Тогда a*= 0,1×ln[(2000×100000)/(10×3000)] = 0,011 - в этих случаях дефектное (негодное) изделие будет признано годным.
5.10 Анализ и оптимизация систем управления запасами
Под системой управления запасами (СУЗ) понимается система фирмы, которая обеспечивает какими-либо ресурсами (устройствами, сырьём, деталями) производственный процесс. В упрощенном виде – это служба снабжения со складами. Весь запас ресурса – это омертвлённый капитал, его оптимальный уровень определяет качество службы менеджмента.
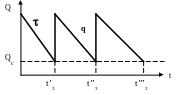
Рисунок 5.4 – График потребления и пополнения ресурса
Пусть нужно в каждый момент времени иметь такое количество ресурса Q, чтобы потери были наименьшие.
Пример 5.6. 1. Исходные данные. Пусть годовая потребность фирмы Qг составляет 1300 шт./год, стоимость одного устройства p=6,5 рублей/шт. При осуществлении одного заказа (объём заказа q согласован с поставщиком) фирма несёт определённые затраты А=5 рублей/заказ, стоимость хранения одного устройства Cхр=0,2 руб./год. Устройства поставляются после заказа немедленно.
2. Сформулируем функцию суммарных затрат Z одного заказа.
Z = A ×(Qг /q) + 0,5× Cхр×q ® min
Производная dz/dq = – A× Qг ×q-2 + 0,5×Cхр, откуда при dz/dq = 0 получаем оптимальную величину заказа q* =[ 2×A× Qг / Cхр ]1/2 = [ 2×5×1300 / 0,2]1/2 = 255 шт.
Количество заказов Qг / q* = 1300/255 = 5 раз в год.
Цикл заказа tзаказа = 365/5 =73 дня.
Более подробно проблемы закупочной логистики управления запасами рассмотрены в работах [8, 13, 14].
Задача 5.1. Результаты стратегий S1S4 работы фирмы в разных условиях V1V4 среды (с учётом вероятности их проявления) представлены в таблице 5.8. Какая стратегия является наилучшей и почему?
Таблица 5.8 - Результаты стратегий
-
Стратегии
Среда и её вероятность
V1 (p1=0,1)
V2 (p2=0,2)
V3 (p3=0,4)
V4 (p4=0,3)
S1
10
8
6
5
S2
12
10
8
8
S3
10
10
10
6
S4
18
14
6
2