14. Логика высказываний. Предикаты, операции, свойства операций.

15. Отображения, функции.

Функции отображения

Особое внимание в матетматике уделяют понятию функции соответствия.

Функции (f)– соответствие f(X,Y,Г) называются функции, если для любых элементов х из множества Х и У из множества У xfy₁, xfy_2, y₁=y₂.

При этом множество х называется областью определения функции, а у – множество значений функции.

Способы задания функции:

1. Табличный

2. Аналитический (наиболее распространенный). Задавая аналитическую функцию фактически посредствам условной записи формулируем или задаем алгебраическую и неалгебраическую операцию посредством которой связаны ч и у.

3. Графический. Множество пар графика функции соответствия можно изобразить в виде точек функции множество, при этом точки могут представлять кривую, которая при определенных функциях задает функцию.

16. События и их классификация.

Под опытом или испытанием будем понимать всякое осуществление комплекса условий или действий, при которых наблюдается интересующее нас явление. Возможный результат опыта (или опытов, если они повторяются многократно) называют событием.

Событие называют достоверным, если оно обязательно произойдет при испытании. Если в результате испытания событие не может произойти, то его называют невозможным. Случайным будем называть такое событие, которое в результате испытания может произойти или не произойти. Случайные события обозначают прописными буквами латинского алфавита Достоверное событие обозначим буквой 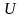, а невозможное — буквой .

Два события называют совместными в данном опыте, если появление одного из них не исключает возможности появления другого в этом опыте, и — несовместными, если они не могут произойти вместе при одном и том же испытании.

Несколько событий в данном опыте будем называть попарно несовместными (или просто несовместными), если любые два из них несовместны.

Будем говорить, что несколько событий образуют полную группу, если они попарно несовместны и в результате испытания непременно произойдет одно из них.

Два события, образующие полную группу, называются противоположными. Для любого события противоположное событие будем обозначать (читается “не ”).

Равновозможными назовем такие события, когда нет основания полагать, что одно из них является более возможным, чем другие.

17. Классическое определение вероятности. Статистическое понятие вероятности.

С каждым испытанием, вообще говоря, могут одновременно наступить несколько интересующих нас событий. Например, при одном бросании игрального кубика события “выпало четыре очка” и “выпало четное число очков” не исключают друг друга. Все возможные, исключающие друг друга, результаты одного испытания будем называть элементарными исходами (или элементарными событиями) испытания.

Пусть — полная группа равновозможных элементарных исходов испытания. При некоторых исходах событие наступает, при других — не наступает. Исходы, при которых событие наступает, будем называть благоприятствующими событию  .

Вероятностью события , обозначаемой , называется отношение числа элементарных исходов испытания, благоприятствующих событию , к числу всех равновозможных и образующих полную группу элементарных исходов, то есть

Классическое определение вероятности предполагает, что число элементарных исходов испытания является конечным и эти исходы равновозможны. Однако на практике весьма часто встречаются испытания с бесконечным числом возможных исходов. Кроме того, часто невозможно результат испытания, даже с конечным числом исходов, представить в виде совокупности равновозможных элементарных исходов.

Ввиду этого наряду с классическим определением вероятности пользуются статистическим, которое часто бывает более удобным для приложений.

Пусть производится однотипных испытаний, в которых может появиться событие

Относительной частотой (или частостью) события  обозначаемой называется отношение числа опытов, в которых появилось событие к числу всех проведенных опытов, то есть

Оказывается, что по мере увеличения числа испытаний значения относительных частот события изменяются мало, устойчиво колеблясь при этом около некоторого постоянного числа причем эти отклонения тем меньше, чем больше число испытаний. Это число и называется вероятностью события в статистическом смысле.

Таким образом, при статистическом определении за вероятность события принимают его относительную частоту или число, близкое к ней.