1. Множества.

Множество – совокупность объектов, объединённых по некоторому признаку.

Обозначают – А, В, С, …

Объект, принадлежащий множеству, называется элементом множества.

Обозначают – а, в, с,…

а А , а А

2. Способы задания множеств. Равные множества.

- перечислением элементов:

А={а, в, с, d}

- указанием характеристического свойства

А и В называются равными, если они состоят из одних и тех же элементов (А=В)

Критерий равенства множеств:

А=В тогда и только тогда, когда А В и В А.

Множество называется пустым, если оно не содержит ни одного элемента.

Обозначают

3. Подмножества. Диаграммы Эйлера-Венна.

Если каждый элемент множества В является также элементом множества А, множество В называется подмножеством множества А (обозначение - B ⊆ A или A ⊇ B).

Диаграмма Эйлера-Венна - наглядное средство для работы со множествами. На этих диаграммах изображаются все возможные варианты пересечения множеств. Количество пересечений (областей) n определяется по формуле: n=2N, где N - количество множеств. Таким образом, если в задаче используется два множества, то n=22=4, если три множества, то n=23=8, если четыре множества, то n=24=16. Поэтому диаграммы Эйлера-Венна используются в основном для двух или трех множеств. Множества изображаются в виде кругов (если используется 2-3 множества) и эллипсов (если используется 4 множества), помещенных в прямоугольник (универсум).

Диаграмма Эйлера-Венна - наглядное средство для работы со множествами. На этих диаграммах изображаются все возможные варианты пересечения множеств. Количество пересечений (областей) n определяется по формуле:

n=2^N, где N - количество множеств.

Таким образом, если в задаче используется два множества, то n=2²=4, если три множества, то n=2³=8, если четыре множества, то n=2⁴=16. Поэтому диаграммы Эйлера-Венна используются в основном для двух или трех множеств.

Множества изображаются в виде кругов (если используется 2-3 множества) и эллипсов (если используется 4 множества), помещенных в прямоугольник (универсум).

4. Пересечение множеств.

Пересечением А В называется множество, состоящее из элементов, принадлежащих каждому из множеств А и В.

А В = {x l x A и x }

5. Объединение множеств.

Объединением А В называется множество, состоящее из элементов, принадлежащих хотя бы одному из множеств А или В.

А В = {x l x A или x }

6. Дополнение к множеству. Свойства. Разность множеств.

Разностью А \ В называется множество, состоящее из элементов А, не принадлежащих В.

А \ В={x l x A и x }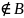

Дополнением называется множество, состоящее из элементов А, не принадлежащих В, если В А.

B_A’ = {x | x A и x В А}

B’ – дополнение до универсального множества

7. Кортеж. Декартово произведение множеств.

Кортеж – совокупность объектов, объединённых по некоторому признаку в определённом порядке.

Обозначают: (а₁, а₂, …, а_n)

Длина кортежа – число его элементов.

(a;b) – упорядоченная пара.

(а;b) ≠(b;a)

Декартовым произведением А называется множество пар (а;b) таких, что а А и b В.

АВ={(a;b) l a A и b B}

Декартовым произведением

… называется множество кортежей ( , , …, ) таких, что , , …,

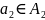… = {( , , …, ) l , , …, }