4.5 Вычисления стационарного распределения

Случайная устойчивость говорит нам, что состояния выживают с положительной вероятностью, когда фоновый шум исчезающе мал, но она не говорит, как вероятны эти состояния, когда шум всего лишь "небольшой". Априори мы не можем сказать, сколько "обоснованного' шума, так как это зависит от приложения под рукой. Отсутствие такой оценки представляет интерес спросить, как тесно стационарные распределения ɱ приближается к его асимптотическому пределу, когда уровень шума положителен. В этом разделе мы покажем, как получить точную оценку распределения ɱ для игры 2x2, что дает ощущение, как сильно случайно устойчивое равновесия выбрано в случае, когда шум небольшой, но не исчезающе мал. Удивителен ответ тем, что выбор может быть резким даже для значительных значений ε (например,. е = .05, или .10) так долго, пока численность населения также велика. Причина этого вскоре станет очевидным.

Рассмотрим однопопуляционную обучающую модель для симметричной координационной игры 2х2 в (4,4). Мы должны определить состояние k^t в момент времени t с числом агентов, играющих действие 1; таким образом, пространство состояний является одно-

Рисунок 4.1. Уникальное k-дерево с ненулевой вероятностью для данного состояния k.

мерным. Пусть (ɣ, 1 - ɣ) – смешанное стратегическое равновесие для каждого игрока, то есть, у = (b-c) / (a - d + b - c). Предположим, что ɣ <1/2, то есть равновесие (1, 1) строго рискодоминирующее. Будет удобно считать, что выборка является полной (s = m), то есть каждый игрок реагирует на все распределение, включая его самого. Пусть 0 < k^t < m – состояние в период t (число агентов, играющих действие 1). Предположим, что с вероятностью 1 - ε, игрок, выбранный в период t +1 выбирает лучший ответ на распределение вероятностей (k^t / m, 1 - k^t / m) и что, с вероятностью ε, он случайно выбирает стратегию 1 или 2, каждая с вероятностью ε / 2. Фиксируем ε ∈ (0,1). Пусть P^m "обозначает матрицу перехода этого процесса, то есть, p^m_kk есть вероятность перехода из состояния k к состоянию k' в одном периоде. Обратите внимание, что процесс либо остается в том же состоянии, либо перемещается в соседнее состояние: P^m_kk˃ 0 только если k' = k – 1 или k + 1. Вероятности перехода являются:

Так как единственно возможный однопериодный переход в соседние состояния (или в то же состояние) каждое состояние k связано только с одним k-деревом с ненулевой вероятностью, а именно дерево T_k, в котором все ребра лежат на линии и направлены к k (см. рис 4,1).

Зафиксируем ε ∈ (0,1). Для каждого натурального m, пусть ɱ^m (к) обозначим как единственное стационарное распределение процесса P^m на пространстве состояний 0 ≤ k ≤ m. По лемме 3.1, ɱ^m(к) пропорциональна произведению вероятностей на краях уникального k – дерева T_k. Мы утверждаем, что, когда m достаточно велико, ɱ^m(к) ставит почти все вероятности состояния k таким, что k / m близко к 1 - ε / 2. Чтобы установить это, давайте расширим (4,10) путем определения вероятности правого и левого переходов для каждого действительного числа ɯ ∈ [0,1] следующим образом:

Для каждого ɯ ∈ [0,1], определим

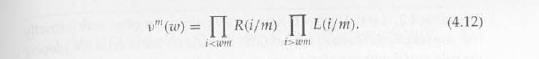
где i пробегает целые 0,1,2… m. Отметим, что для целого k, v^m (k / m) равна произведению вероятностей перехода краев в уникальном k – дереве T_k, следовательно, v^m (k / m) пропорционально ɱ^m(к). Мы будем изучать форму v^m (.), когда m становится большим. Из (4.12) имеем

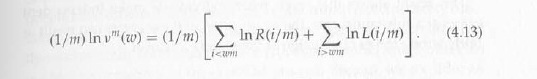
Для каждого ɯ ∈ [0,1] определим функцию V (ɯ) следующим образом:

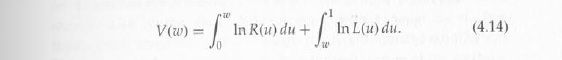
Затем

и сходимость равномерна на [0, 1]. В сущности, - V (ɯ) является случайным потенциалом состояния ɯ когда m – численность населения стремится к бесконечности и ставка ошибки ε является фиксированной. (Эта конструкция является достаточно общей и работает для широкого спектра одномерных процессов).

Пусть ɯ* - точка, в которой V(ɯ) достигает своего максимума. Условие первого порядка V'(ɯ*) = 0, которое имеет место тогда и только тогда, когда R (ɯ*) = L (ɯ*). Существуют два решения: ɯ* = 1 - ε / 2 и ɯ* = ε / 2. Прямая оценка (4,14) показывает, что ɯ*= 1-е / 2 является единственным глобальным максимумом. Для каждого маленького δ > 0 пусть F_δ = {ɯ: |ɯ - ɯ*|> δ} и N_δ/2 = {ɯ: |ɯ - ɯ*|≤ δ/2}. Тогда sup{ V(ɯ): ɯ ∈ F_δ } < inf{V(ɯ): ɯ ∈ N_δ/2 } и

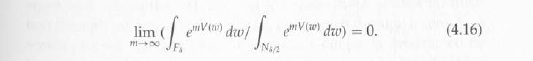
Отсюда и из (4,15) мы заключаем, что v^m(.), а также ɱ^m(.) концентрируются в δ-окрестности ɯ* = 1 -ε / 2 для всех достаточно больших m, то есть

Нт цт ({к: | к / ​​т - (1 - 6/2) | <6)) = 1. (4.17)

Резюмируем это в следующий результат.

Теорема 4.1 Пусть G – симметричная координационная игра 2 х 2 со строгим рискодоминирующим равновесием и пусть Q^m – адаптивное изучение в модели полевой игры размера m, полной выборкой и ставкой ошибки размера ε, 0 < ε <1. Для каждого ε' > ε вероятность сколь угодно высока, что не менее 1 - ε'/2 населения играет рискодоминирующее равновесие, когда m достаточно велико.

Этот результат показывает, что, даже когда люди делают независимые ошибки в существенных темпах, агрегация этих ошибок может привести к довольно мощной силе выбора на популяционном уровне.