Выполнила: студентка 123 группы,

Шатилова Анастасия.

Глава 4

Адаптивное обучение в маленьких играх

В ЭТОЙ ГЛАВЕ мы исследуем свойства адаптивного обучения в играх на две персоны, где каждый игрок имеет ровно два действия. Хотя это особый случай, он может быть использован для отображения широкого спектра социальных и экономических взаимодействий. Мы начнем с введения классическое понятие риска доминирования в игре 2х2, а затем покажем, что она совпадает со случайно стабильным результатом при различных предположениях о процессе обучения. В играх побольше, однако, эти два понятия различаются, как мы увидим в главе 7.

4.1 Доминирование риска

Рассмотрим игру двух лиц G с платежной матрицы

G - координационная игра с чистой стратегией равновесия Нэша (1,1) и (2,2), если и только если выплаты удовлетворяют неравенствам

Равновесие (1.1) есть рискодоминирующее, если

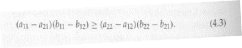
Аналогичным образом, равновесие (2, 2) является доминирующим риском, если обратное неравенство (Харсаньи и Сэлтен, 1988). Если неравенство строгое, то соответствующее равновесие строго рискодомонирующая.

Доминирование риска имеет простую интерпретацию, особенно когда игра является симметричной. Рассмотрим симметричную матрицу выигрышей

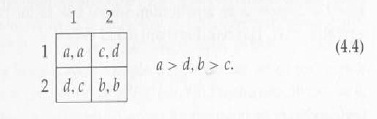
Представьте себе, что каждый игрок не уверен, что другой игрок собирается совершить. Придадим вероятность пятьдесят на пятьдесят действиям других. Ожидаемый выигрыш от игры в действии 1 (А + С)/2, в то время как ожидаемый выигрыш от действий 2 (D + B )/2.Ожидаемая полезность максимизируется, поэтому выбирается действие 1, причем только тогда, когда (А + C) / 2≥ (D + B) / 2, то есть, только если A-D≤B-C. Это равносильно тому, что действие 1 является рискодоминирующим. Другими словами, когда каждый игрок имеет равные шансы на действия 1 или 2 его или ее соперника, оба игрока выберут рискодоминирующие действия.

В более общем случае (4,1), мы можем мотивировать доминирования риска следующим образом. Определим фактор риска равновесия (i, i), где i=1,2, чтобы наименьшая вероятность р была такой, что если один игрок считает, что другой игрок собирается совершить действие i с вероятностью строго больше, чем р, то i – это единственное оптимальное для совершения действие. Рассмотрим, например, равновесие (2,2). Для ряда игроков, наименьшее р удовлетворяет

то есть,

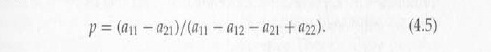
Для игрока столбца, наименьшее из таких р удовлетворяет

то есть,

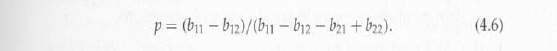
В общем, пусть

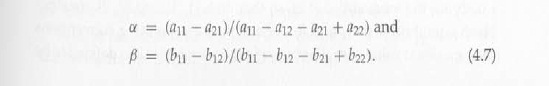
Таким образом, фактором риска для равновесия (2, 2)является α ˄ β, где в общем x ˄ y обозначает минимум х и у. Кроме того, фактором риска для равновесия (1, 1) (1 - α) ˄ (1 - β). Рискодоминирующее равновесие в игре 2х2 есть равновесие, чей фактор риска является самым низким. Таким образом, равновесие (1,1) является рискодоминирующим, если

α ˄ β ≥ (1 - α) ˄ (1 - β)

Равновесие (2, 2) является рискодоминирующим, если выполняется обратное неравенство. Немного алгебраических манипуляций и становится очевидным, что (4,8) эквивалентно

Иными словами, в игре 2 х 2 равновесие является рискодоминирующим, если оно максимизирует выгоду от одностороннего отклонения (Харсаньи и Сэлтен, 1988).

4.2 Случайная стабильность и доминирование рисков в игре 2х2

Напомним, что конвенция – это структура формы (х, х,…, х), где х =(х₁,х₂,…, х_n), являющаяся строгим равновесием G по Нэшу. В таком состоянии каждый будет продолжать играть свою роль в х (без учета ошибок), поскольку х_i является уникальным лучшим ответом, дающим i – ожидания, что все остальные будут играть свою роль в х.

Теорема 4.1. Пусть G есть координационная игра 2 X 2 и пусть P^m,s, ᵋ – адаптивное обучение с памятью M, выборка размера S и ошибка величины ε.

(I) Если информация достаточно неполная (S / M ≤1/2), то из любого исходного состояния спокойный процесс P^{m,s, 0} сходится с вероятностью один к конвенции и блокируется.

(II) Если информация достаточно неполная (S / M ≤1/2) и s и m достаточно велики, случайно устойчивые структуры беспокойного процесса соответствуют один на один рискодоминирующим конвенциям.

Доказательство. Пусть G координационная игра 2 х 2 с платежной матрицей (4,1), удовлетворяющая неравенствам (4,2) так, что и (1, 1), и (2, 2) строгие равновесия по Нэшу. Пусть h₁ и h₂ обозначим как соответствующие соглашения для некоторого фиксированного значения m. Притяжения h₁ определяется как множество состояний h таких, что есть положительная вероятность движения к конечному числу периодов от h до h₁ в спокойном процессе p⁰. Пусть β_i обозначает притяжение h_i, i=1, 2. Чтобы доказать I теорему, мы должны показать, что β₁ и β₂ охватывает пространство состояний.

Пусть h = (x^t-m+1 ,….x’) – произвольное состояние. Существует положительная вероятность того, что оба игрока попробовать определенный набор прецедентов x^t-m+1 в каждый период с t + 1 до t + s включительно. Т.к. ε=0, каждый из них играет лучший ответ. Предположим на минуту, что лучший из ответов является уникальным, скажем, (x*₁, x*₂)=x*. Тогда мы получим перспективу (х*, х*….x*) от периода t + 1 к периоду t + s (если есть связи в лучшем ответе для некоторых игроков, то по-прежнему существует положительная вероятность, что та же пара лучших ответов (x*₁, x*₂)=x* будет выбрана для периодов s, потому что все лучшие ответы имеют положительную вероятность быть выбраными). Заметим, что этот аргумент использует предположение, что s ≤ m/2. Если s слишком велико по отношению к m, некоторые из прецедентов x^t-m+1 ,….x’ "вымрут" к периоду t + s, что противоречит нашему предположению о фиксированном наборе прецедентов для периодов s.

Предположим, что с одной стороны х* является координацией равновесия, то есть х * = (1,1) или х * = (2,2). Существует положительная вероятность того, что, с периодом t + s + 1 через период t +m оба игрока будут совершать действия сразу же. Уникальный лучший ответ на i с любого такого образца х_i* (i = 1,2). Таким образом, к концу периода t +m существует положительная вероятность того, что процесс достигнет соглашение (x*, x*,….x*).

Предположим, с другой стороны, что х * не является координацией равновесия. Тогда х * = (1,2) или х * = (2,1) Без ограничения общности считаем, что х * = (1,2) Существует положительная вероятность того, что от периода t + s + 1 через период t + 2s , строка игроков в дальнейшем будет придерживаться последовательности (x^t-s+1 ,….x’) и играть 1 как лучший ответ. Существует также положительная вероятность того, что одновременно колонка игроков будут попробовать сразу и, следовательно, будут играть 1 как лучший ответ. Таким образом, с периодом t + s + 1 через период t + 2s, мы получим формы (1,1), (1,1), .... (1,1). С этого момента становится ясно, что с положительной вероятностью процесс сходится к конвенции h₁.

Таким образом, мы показали, что из любого исходного состояния существует положительная вероятность достижения h₁ и/или h₂ в конечном числе периодов.

Чтобы установить утверждение (II), применяем теорему 3.1. Пусть г^s₁₂ – наименьшее сопротивление среди всех путей с h₁ и до h₂ функции с размером выборки. Очевидно, что это так же, как наименьшее сопротивление среди всех путей, которые начинаются в h₁ и заканчиваются в ϐ₂, потому что после ввода ϐ₂ не нужно никаких дальнейших ошибок, необходимых для достижения г^s₁₂.

Пусть α и β определены, как в (4,7). Кроме того, пусть [у] обозначим как наименьшее целое число, большее или равное у для любого вещественного числа у. Предположим, что процесс находится в состоянии поглощать h₁, где оба игрока строки и столбца выбрали действие 1 на m периодов подряд. Для игрока столбца чтобы предпочесть действие 2 действию 1, должна быть по крайней мере [αs] случаев действия 2 в образце игрока строки. Это произойдет с положительной вероятностью, если последовательность [αs] игроков колонки выберут действие 2 по ошибке. (Заметим, что при этом используется предположение, что все образцы взяты с положительной вероятностью.) Вероятность этих событий ε^[αs]-порядка. Аналогично, игрок колонки предпочитает действие 2 действию 1 только, если существует по крайней мере [αs] случаев действия 2 в образце игрока колонки. Это произойдет с положительной вероятностью, если последовательность [βs] игроков колонки выберите действие 2 по ошибке, которая имеет вероятность порядка ε^[βs].

Отсюда следует, что переход от h₁ к h₂ есть r^s₁₂ = [αs] ˄ [βs] Простые вычисления показывают, что r^s₂₁ = [(1-α)s] ˄ [(1-β)s]. По теореме 3.1 h₁ случайно устойчив тогда и только тогда, когда r^s₁₂≥ r^s₂₁; аналогично h2 случайно устойчиво тогда и только тогда, когда r^s₁₂ ≤ r^s_21. Если одно равновесие строго рискодоминирующее, скажем, равновесие (1, 1. ), то r^s₁₂ ˃ r^s₂₁ для всех достаточно больших s, поэтому соответствующие конвенции является случайно устойчивый. Предположим, с другой стороны, что два равновесия делят риск доминирования. Тогда α = 1 - β и r^s₁₂ = r^s₂₁ для всех s, так как h₁ к h₂ случайно стабильны. Это завершает доказательство теоремы 4.1.

Мы не утверждаем, что незавершенность, связанная с s/m ≤ 1/2 является наилучшим, но некоторая степень неполноты, необходимой для части (I) теоремы 4.1, выполняется. Чтобы понять почему, рассмотрим этикет игры, описанной в главе 2. Пусть s = m и предположим, что процесс начинается в рассогласованном состоянии, в котором либо оба игрока всегда имеют пользу в периоде s, либо они всегда неуспешны. Из-за реакции игроков на полную историю и нулевого уровня, они уверены, что рассогласуются снова. Этот рассогласованность продолжается вечно, и этот процесс никогда не достигает поглощающего состояния. Заявление (i) теоремы утверждает, что такое циклическое поведение не может произойти, когда информация является достаточно полной, потому что неполная выборка обеспечивает достаточно случайные изменения (даже без ошибок), чтобы вытряхнуть процесс из цикла.