7.3 Виды и методы измерений геометрических параметров изделий

Существуют различные виды и методы измерений.

Виды измерений классифицируют по следующим признакам:

- физическая сущность измеряемых физических величин;

- характеристика точности (измерения равноточные, неравноточные);

- число измерений случайной величины (измерения однократные, многократные);

- измерение определяемой величины во времени (измерения статические, динамические);

- метрологическое назначение (измерения технические, метрологические);

- способ получения числового значения физической величины (прямые, косвенные, совместные, совокупные);

- выражение результатов измерений (измерения абсолютные, относительные).

Равноточные измерения – ряд измерений какой-либо величины, выполненными одинаковыми по точности средствами измерений и в одних и тех же условиях с одинаковой тщательностью. Например, измерение у детали одного и и того же размера разными микрометрами одинаковой точности при одинаковой температуре и влажности помещения, в котором производят измерения.

Неравноточные измерения – ряд измерений какой-либо величины, выполненными различающимися по точности средствами измерений и (или) в разных условиях. В этом случае размер одной и той же детали определяется в разных условиях (например, в разных цехах) или разными средствами измерений (например, в одном цехе штангенциркулем, а в другом микрометром), разными операторами.

Однократное измерение – измерение, выполненное один раз.

Многократное измерение – измерение одной и той же физической величины, результат которого получен из нескольких следующих друг за другом измерений (наблюдений), т.е. измерение, состоящее из ряда однократных измерений.

Метрологические измерения – измерения, выполненные при помощи рабочих эталонов и образцовых средств измерения.

Технические измерения – измерения, выполненные при помощи рабочих средств измерения.

При прямом измерении искомое значение величины находят непосредственно из опытных данных. При­мерами прямых измерений являются измерения длины с помощью линей­ных мер или температуры термометром. Прямые измерения составляют основу более сложных – косвенных.

При косвенном измерении искомое значение величины находят на основании известной зависимости меж­ду этой величиной и величинами, подвергаемыми прямым измерениям, например тригонометрические методы измерения углов, при которых острый угол прямоугольного треугольника определяют по измеренным длинам катетов и гипотенузы.

Совместные измерения – одновременные измерения двух или нескольких разнородных величин для установления зависимости между ними (ряд одновременных, прямых измерений электрического сопротивления проводника и его температуры для установления зависимости сопротивления от температуры).

Совокупные измерения – проводимые одновременно измерения нескольких одноименных величин, при которых искомое значение величин находят решением системы уравнений, получаемых при прямых измерениях различных сочетаний этих величин (нахождение значений массы отдельных гирь набора по известному значению массы одной из гирь: сравнивая массы различных сочетаний гирь, получают систему уравнений, из решения которой находят массу одной из гирь, входящих в набор).

Абсолют­ные измерения основаны на прямых измерениях одной или нескольких основных величин, то есть по шкале прибора определяется полное значение измеряемой величины.

Относительные измерения основаны на измерении отношения величины к одноименной величине, играющей роль единицы, или измерения величины по отношению к одноименной величине, принимаемой за исходную.

Метод измерений – совокупность приемов, обеспечивающих сравнение измеряемой физической величины с её единицей (мерой).

Методы измерений основаны на физических принципах взаимодействия объекта измерения и средств измерения для получения измерительной информации с допустимой погрешностью.

Методы измерений различают:

1. по физическому принципу измерения (механические, пневматические, акустические, оптические, электрические и т.п.);

2. по виду измерительных сигналов в средствах измерения (аналоговые (соответствующая функция непрерывна) и цифровые (функция квантуется));

3. по способу сопоставления измеряемой физической величины и меры, различают метод непосредственной оценки и методы сравнения.

Наиболее распространен метод непосредственной оценки, в нем о физической величине судят по показаниям одного (прямые измерения) или нескольких (косвенные измерения) приборов, которые заранее проградуированы в единицах измеряемой величины.

В методах сравнения измеряемая величина сопоставляется с мерой, которая находится вне средств измерения.

Различают дифференциальный метод, где об измеряемой величине судят по её разности с каким-либо эталоном.

Рассмотрим U-образный жидкостный манометр, измеряемой величиной является давление P_x (рис. 7.3).

Давление P_x находится по формуле:

P_x=P_H+ρgh. (7.2)

Если P_x>P_H, то соответствующая жидкость выдавливается в трубку, соединенную с мерой (эталоном).

Рисунок 7.3 – U-образный манометр

В дифференциальных методах мы предполагаем, что эталон, с которым сравнивается измеряемая величина, находится более точно, чем сама величина - P_x, поэтому ошибка будет заложена в измерении ρgh, а точнее, т. к. довольно точно известны плотность и ускорение свободного падения, то вся погрешность располагается в измерении высоты - h, и чем, больше эта высота, тем меньше погрешность.

Разность между P_x и P_H должна быть как можно меньше, следовательно, высоту h нужно увеличить, например при измерении давления в камере сгорания ракетного двигателя это достигается с помощью уменьшения плотности - ρ - вместо воды используется масло, или наклона плеча пьезометр, если погрешность измерения высоты составляет примерно 1 мм при наличии трубки высотой в 1,5 м, то погрешность будет 1мм/1500. В настоящее время давление окружающей среды - P_H измеряется с высокой точностью, поэтому дифференциальный метод позволяет значительно более точно измерить давление P_x , чем прямым образом, т. е. с использованием манометра.

Разновидностью дифференциального вида является нулевой метод, когда средство измерения при нагружении его измеряемой величиной возвращается в исходное положение.

В рассматриваемом примере величина ρgh→0, т. к. h=0. Гистерезис отсутствует, левое плечо столба уходит в правое, из - за поверхностного натяжения жидкость остается на стенках и, естественно, что показания прибора искажаются, если уравновесить давление P_x, т. е. давление P_H заменить переменным давлением, которое можно достаточно точно измерить, то столбики вернутся в исходное положение, и параметры диссипации энергии будут отсутствовать.

Нулевой метод более точный, т. к. погрешность сосредоточена преимущественно в эталоне, т. е. какова погрешность эталона, такова и погрешность данного метода.

В методе замещения об измеряемой величине судят по изменению измерительного сигнала при замене объекта измерения эталоном.

Рассмотрим нагруженный динамометр, который проградуирован в единицах массы (рис. 7.4).

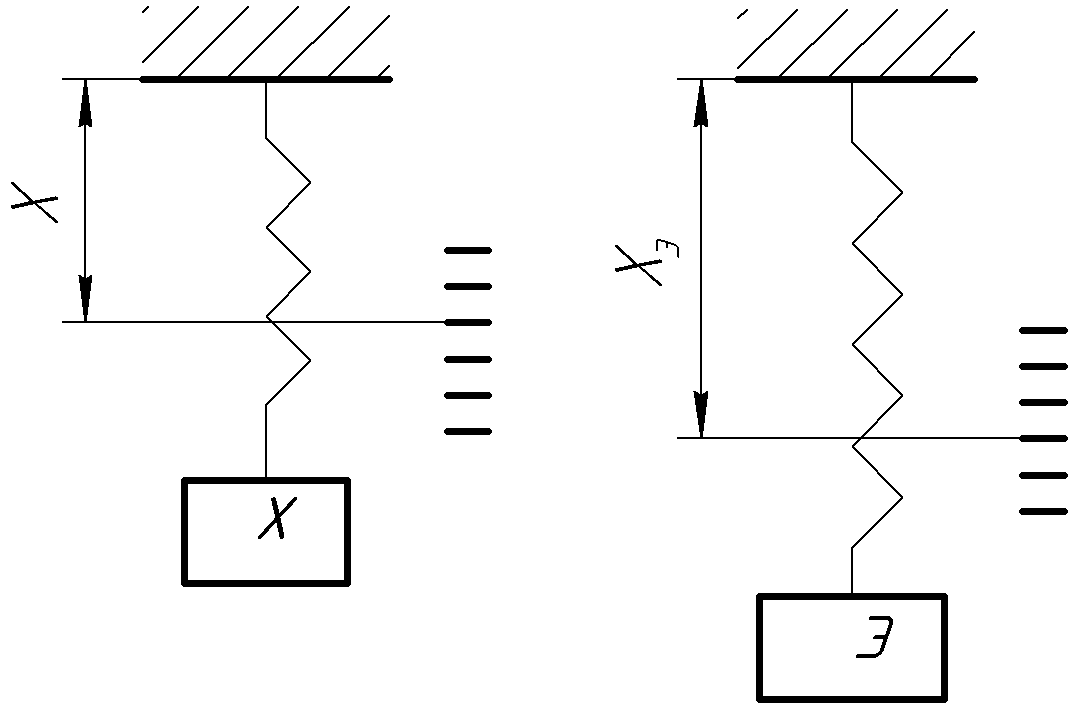
Рисунок 7.4 – Метод замещения:

Х – измеряемая величина, Э – эталон

Вместо измеряемой величины нагружаем средство измерения эталоном.

Об измеряемой величине судим по соотношению:

X / X_э, (7.3)

чем ближе эталон к измеряемой величине, тем точнее будет измерение.

В методе совпадений разность между измеряемой величиной и воспроизводимой мерой определяется с помощью совпадения каких – либо периодических сигналов, например отметок шкалы (штангенциркуль).