34. Теплопроводность через однослойную цилиндрическую стенку при граничных условиях III-го рода.
Р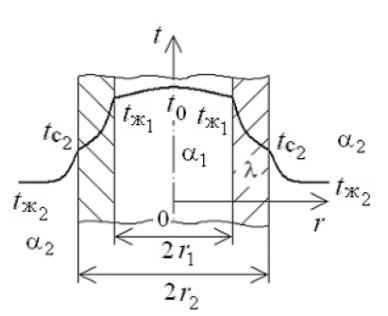
ассмотрим
однородную цилиндрическую стенку
(трубу) с внутренним диаметром
d1
и наружным диаметром d2
(рис.
1) с
постоянным коэффициентом теплопроводности
λ.
Заданы постоянные температуры подвижных
сред tЖ1
и tЖ2,
а также постоянные значения коэффициентов
теплоотдачи на внутренней и наружной
поверхностях трубы α1
и
α2.
Необходимо найти температуры поверхностей
цилиндрической стенки tС1
и
tС2
и тепловой поток через нее.
Будем полагать, что длина трубы велика по сравнению с толщиной стенки. Тогда потерями тепла с торцов трубы можно пренебречь и при установившемся тепловом режиме количество тепла, которое будет передаваться от горячей среды к поверхности стенки, проходить через стенку и отдаваться от стенки к холодной жидкости, будет одно и то же. Так же, как в случае плоской стенки, выразим плотности теплового потока для теплопроводности и двух процессов теплоотдачи. Выразим температурные напоры и почленно сложим уравнения: tЖ1 – tЖ2 = ql/π*((1/(α1*d1)+(1/2* λ)*ln(d2/d1)+(1/(α2*d2)).
Тогда линейная плотность теплового потока определяется как: ql = π*(tЖ1 – tЖ2)/ ((1/(α1*d1)+(1/2* λ)*ln(d2/d1)+(1/(α2*d2)).
Обозначим выражение: kl = (1/(α1*d1)+(1/2* λ)*ln(d2/d1)+(1/(α2*d2),
Тогда уравнение теплопередачи запишется так: ql = π*(tЖ1 – tЖ2)/Rl.
Величина kl называется линейным коэффициентом теплопередачи. Она характеризует интенсивность передачи тепла от одной подвижной среды к другой через разделяющую их стенку. Значение kl численно равно количеству тепла, которое проходит через стенку трубы длиной один метр в единицу времени от одной жидкой среды к другой при разности температур между ними в один градус. Величина Rl = 1/ki, обратная коэффициенту теплопередачи, называется линейным термическим сопротивлением теплопередачи: Rl =(1/(α1*d1)+(1/2* λ)*ln(d2/d1)+(1/(α2*d2), ([м*К)/Вт]. Отдельные составляющие полного термического сопротивления представляют: Rl1 = 1/(α1*d1) и Rl2 = 1/(α2*d2) – линейные тепловые сопротивления теплоотдачи на соответствующих поверхностях; Rlс =(1/2* λ)*ln(d2/d1) - линейное тепловое сопротивление теплопроводности стенки.
В отличие от термических сопротивлений теплоотдачи для плоской стенки здесь термические сопротивления теплоотдачи зависят не только от коэффициента теплоотдачи, но и от диаметра стенки. Если тепловой поток через цилиндрическую стенку отнести к внутренней или наружной поверхности стенки, то получим плотность теплового потока, отнесенную к единице соответствующей поверхности трубы: q1 = Q/(π*d1*l) = (kl /d1)*(tЖ1 – tЖ2), а в свою очередь: q2 = Q/(π*d2*l) = (kl/d2)*(tЖ1 – tЖ2). Обозначим k1 = kl /d1 и k2 = kl /d2 , тогда kl = k1*d1 = k2*d2, следовательно, q1 = k1*(tЖ1 – tЖ2) и q2 = k2*(tЖ1 – tЖ2).
Температуры поверхностей цилиндра: tС1 = tЖ1 – (ql / π)* 1/(α1*d1) и tС2 = tЖ2 + (ql / π)* 1/(α2*d2). В случае теплопередачи через многослойную цилиндрическую стенку линейная плотность теплового потока определяется как:
ql = π*(tЖ1 – tЖ2)/( 1/(α1*d1)+(1/2)*∑(1/λi)*ln(d(i+1)/di)+ 1/(α2*dn+1), [Вт/м]
или ql = π*kl*( tЖ1 – tЖ2).
Величина Rl называется полным термическим сопротивлением теплопередачи многослойной цилиндрической стенки и равна: Rl = 1/ kl = ( 1/(α1*d1)+(1/2)*∑(1/λi)*ln(d(i+1)/di)+ 1/(α2*dn+1).
Температуры стенок: tC(m+1) = tЖ1 – (ql / π)* (1/(α1*d1)+(1/2)*∑(1/λi)*ln(d(i+1)/di)).
Критический диаметр цилиндрической стенки: Линейное термическое сопротивление теплопередачи через цилиндрическую стенку: Rl =(1/(α1*d1)+(1/2* λ)*ln(d2/d1)+(1/(α2*d2), ([м*К)/Вт]. Исследуем функцию вида: Rl = Rl (d2). Функция непрерывна и дифференцируема:
dRl /d(d2) = 1/(2π*d2) – 1/(α2*d22) = 0. Найдем критическую точку: 1/d2 = (1/2λ -1/(α2*d2)) =0, тогда d2 = 2λ/α2 – это критическая точка.
d2Rl /d(d2)2 = 1/(2λ* d22) + 2/(α2*d23) = 1/d22*(2/ (α2*d2) – 1/2λ).
(2/ (α2*d2) – 1/2 λ) = 2α2/(α2*2λ) – 1/2λ = 1/λ*(1-0,5) = 0,5λ>0, т.о. при d2 = 2λ/α2, термическое сопротивление цилиндрической стенки минимальное.