3 3. Теплопроводность через однослойную цилиндрическую стенку при граничных условиях I-го рода.
Рассмотрим стационарный процесс теплопроводности в бесконечной цилиндрической стенке (трубе) с внутренним диаметром d1 и наружным диаметром d2 (рис. 1) с постоянным коэффициентом теплопроводности λ. На наружных поверхностях трубы поддерживаются постоянными значения температуры tС1 и tС2. Необходимо найти распределение температуры в цилиндрической стенке и тепловой поток через нее. В рассматриваемом случае дифференциальное уравнение теплопроводности удобно записать в цилиндрической системе координат (ось Оz совмещена с осью трубы):
2t
=
=0. Так как
труба бесконечная и изотропная, то
дифференциальное уравнение теплопроводности
примет вид
+
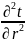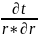= 0. Граничные
условия: при r
=
r1,
t
=
tC1;
при r
=
r2
t
=
tC2.
Если
решить уравнение совместно с условиями,
то получим уравнение температурного
поля в цилиндрической стенке. Задача
решается введением новой переменной:
t = C1*ln(r) + C2. Постоянные интегрирования С1 и С2 можно определить, если в уравнение подставить граничные условия: t = tC1 – (tC1 - tC2)*(ln(r/r1)/ln(r2/r1)). Полученное выражение представляет собой уравнение логарифмической кривой. То обстоятельство, что распределение температуры в цилиндрической стенке является криволинейным, можно объяснить следующим. В случае плоской стенки удельный тепловой поток q остается одинаковым для всех изотермических поверхностей. По этой причине градиент температуры сохраняет для всех изотермических поверхностей постоянную величину. В случае цилиндрической стенки плотность теплового потока через любую изотермическую поверхность будет величиной переменной, так как величина поверхности зависит от радиуса. Для определения количества теплоты, проходящего через цилиндрическую поверхность величиной: F = 2π*r*l в единицу времени, следует воспользоваться законом Фурье: Q = -λ*(dt/dr)*F = (2π* λ*l*(tC1 - tC2))/ln(r2/r1). Из уравнения следует, что количество теплоты, проходящее через цилиндрическую стенку в единицу времени, полностью определяется заданными граничными условиями и не зависит от радиуса. Тепловой поток может быть отнесен либо к единице длины трубы, либо к единице внутренней или внешней поверхности. Тогда расчетные формулы для удельных тепловых потоков примут следующий вид.
Тепловой поток через единицу внутренней поверхности: Q/(π *r1*l) = q1 = (2*λ*(tC1 - tC2))/r1*ln(r2/r1).
Тепловой поток через единицу внешней поверхности:
Q/(π *r2*l) = q2 = (2*λ*(tC1 - tC2))/r2*ln(r2/r1).
Тепловой поток на единицу длины трубы: Q/l = ql = (π*(tC1 - tC2))/((1/2*λ)*ln(r2/r1)). Тепловой поток, отнесенный к единице длины трубы, имеет размерность Вт/м и называется линейной плотностью теплового потока. Как видно из уравнения, при неизменном отношении диаметров линейная плотность теплового потока не зависит от поверхности цилиндрической стенки. Плотности теплового потока через внутреннюю и внешнюю стенки неодинаковы, причем первая больше второй.