Передмова
Метою даних методичних порад є надання допомоги студентам у самостійному вивченні дисципліни «Статистика». Виконання комплексного практичного індивідуального завдання є запорукою оволодіння навичками застосування статистичних методів (методу групування, методу відносних та середніх величин, індексного методу тощо) в процесі статистичного дослідження діяльності суб’єктів господарювання. КПІЗ складено у відповідності з діючою навчальною програмою дисципліни для всіх напрямів підготовки і форм навчання.
Виконання письмового комплексного практичного індивідуального завдання має важливе значення в навчальному процесі, так як сприяє поглибленому вивченню студентом важливих методологічних питань статистики і набуттю практичних навичок при розрахунках статистичних показників, побудові таблиць і графіків, економічній інтерпретації результатів обчислень. КПІЗ охоплює усі основні теми дисципліни «Статистика».
При самостійному вивченні матеріалу потрібно керуватися програмою дисципліни «Статистика» для економічних спеціальностей вищих навчальних закладів і користуватися наведеною в списку літературою.
Комплексне практичне індивідуальне завдання виконується в окремому зошиті, на титульній сторінці якого вказується з якої дисципліни виконується КПІЗ, група, прізвище та ініціали студента, а також номер варіанта завдання, який обирається залежно від порядкового номеру студента за списком.
Комплексні практичні індивідуальні завдання містять десять варіантів. У кожному варіанті міститься десять задач.
Варіанти комплексних практичних індивідуальних завдань
Початкова літера прізвища студента |
Номер варіанта |
А, Б, В |
I |
Г, Д, Е |
II |
Є, Ж, З, І, Ї |
III |
Й, К, Л, М |
IV |
Н, О |
V |
Р, С |
VI |
У, Ф, Х, |
VIІ |
Ц, Ч, Ш, |
VIІІ |
Щ, Ю, Я |
IX |
П, Т |
X |
Завдання виконуються після вивчення навчального матеріалу з відповідних тем дисципліни. Розв’язування задач необхідно викладати повністю, із наведенням усіх необхідних формул, обчислень, проміжних і кінцевих висновків. Результати розрахунків при необхідності слід викладати в табличній формі. КПІЗ повинно бути написане чорнилом або кульковою ручкою, розбірливо, із полями на кожній сторінці для відповідних записів викладача. В кінці наводиться перелік використаної літератури, ставиться дата і особистий підпис студента.
Методичні поради щодо виконання комплексних практичних індивідуальних завдань
Для розв’язання першої задачі кожного варіанта на тему «Зведення і групування статистичних матеріалів» потрібно з’ясувати суть аналітичного групування [26, 27–45], яке вивчає взаємозв’язок між факторною і результативною ознаками. Для цього необхідно визначити, яка з ознак є факторною, а яка – результативною, після чого знайти максимальне й мінімальне значення факторної ознаки, різницю між ними поділити на задану кількість груп. Отримаємо величину інтервалу (і):
,
де
,
– максимальне й мінімальне значення
факторної ознаки;n
– кількість груп, на які необхідно
розбити сукупність.
Нижня межа першої групи дорівнює мінімальному значенню факторної ознаки (Хmin), а верхня межа отримується шляхом додавання величини інтервалу (Xmin+i). Додавши до верхньої межі першої групи величину інтервалу, матимемо верхню межу другої групи і т. д.
Усі розрахунки необхідно виконувати в робочій таблиці, а потім результати перенести у зведену аналітичну таблицю, побудовану за відповідними вимогами [26, 46–73].
У кінці задачі аналізуються дані групової аналітичної таблиці й робляться висновки.
Для розв’язання другої задачі необхідно опрацювати тему «Абсолютні та відносні величини» [26, 74–81].
1. Відносні величини планового завдання – це відношення планової величини до тієї, яка була досягнута на період складання плану.
2. Відносні величини виконання плану – це відношення фактичного виконання завдання до планового (в процентах).
3. Відносні величини структури – це відношення частини до цілого. Вони характеризують структуру суспільного явища.
4. Відносні величини координації – це відношення частин цілого між собою.
5. Відносні величини динаміки характеризують зміни явищ і процесів у часі. Розрізняють відносні величини динаміки з постійною і змінною базами порівняння.
6. Відносні величини інтенсивності характеризують ступінь поширення або розвитку явища в певному середовищі. Їх отримують у результаті порівняння двох різнойменних абсолютних величин, пов’язаних між собою, але які не є додатками або частинами цілого. Вони виражаються іменованими числами.
7. Відносні величини порівняння характеризують співвідношення однойменних величин, які стосуються різних об’єктів, територій, але за один і той же період.
Для розв’язання третьої задачі необхідно обрати вид і форму середньої за економічним змістом показника, який визначається. Наприклад, середню заробітну плату одного робітника визначають шляхом ділення фонду заробітної плати на кількість працюючих. Якщо в умові задачі є дані про заробітну плату одного робітника та їх чисельність, то виходячи з економічного змісту показників для визначення середньої заробітної плати всіх робітників застосовують середню арифметичну зважену:
,
де
–
середня заробітна плата одного робітника;
х –
заробітна плата одного робітника; f
– кількість робітників.
Якщо в умові задачі є дані про фонд заробітної плати й середню заробітну плату одного робітника, то виходячи з економічного змісту цих показників використовують формулу середньої гармонічної зваженої:
,
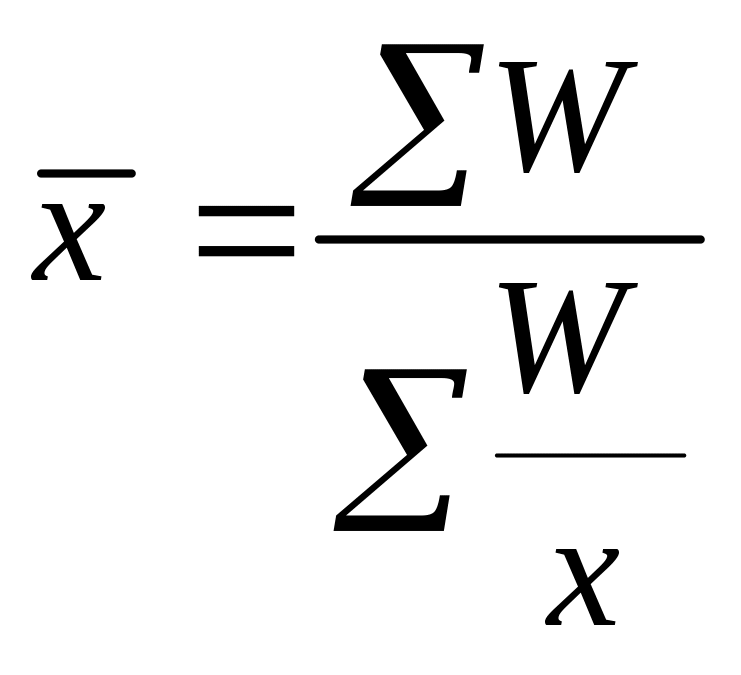де W – фонд заробітної плати.
Аналогічно розраховують інші середні показники [26, 82–95].
Для розв’язання четвертої задачі необхідно засвоїти тему «Показники варіації» [26, 96–105]. Показники варіації розраховуються наступним чином:
Розмах
варіації (
):
.
Середнє
лінійне відхилення (
):
.
Дисперсія
(
):
.
Середня величина (
)
у варіаційному ряді з рівними інтервалами
за способом «моментів» визначається
наступним чином:
,
де
– момент першого порядку,
який розраховується за формулою:
,
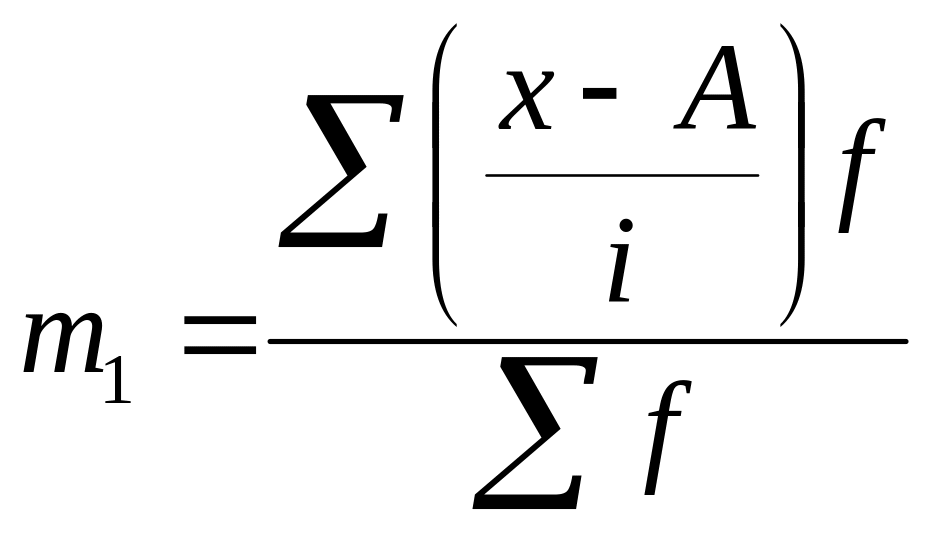де i – величина інтервалу; А – умовне число, переважно середина центрального інтервалу.
Дисперсія (
)за
способом «моментів» розраховується:
,
де
– момент другого порядку
.
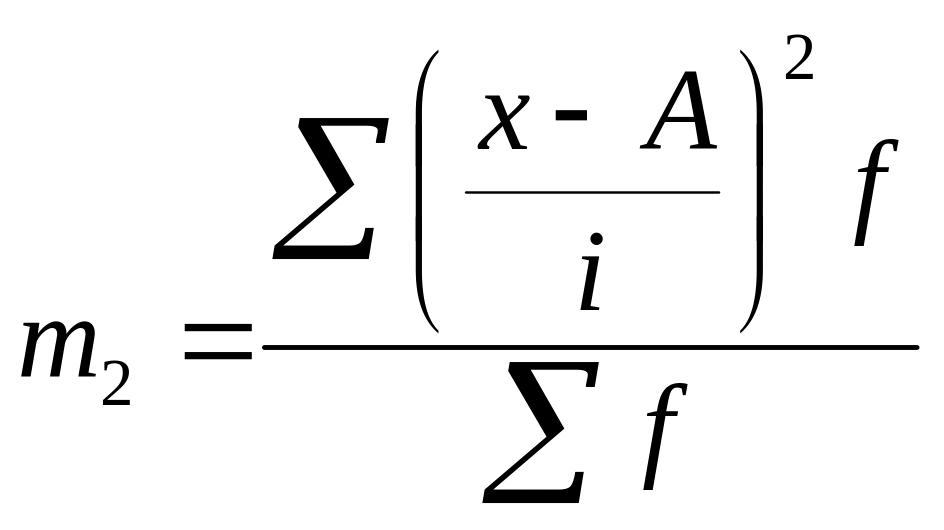Середнє квадратичне відхилення
(
):
.
Коефіцієнт варіації (V):
.
Коефіцієнт
осциляції (
):
.
Відносне
лінійне відхилення (
):
.
Мода
(
)
у варіаційному ряді розраховується за
формулою:
,
де
– нижня межа модального інтервалу; і
– величина
модального інтервалу;
– передмодальна частота;
– модальна частота;
– післямодальна частота.
Медіана
(
)
у варіаційному ряді розраховується
таким чином:
,
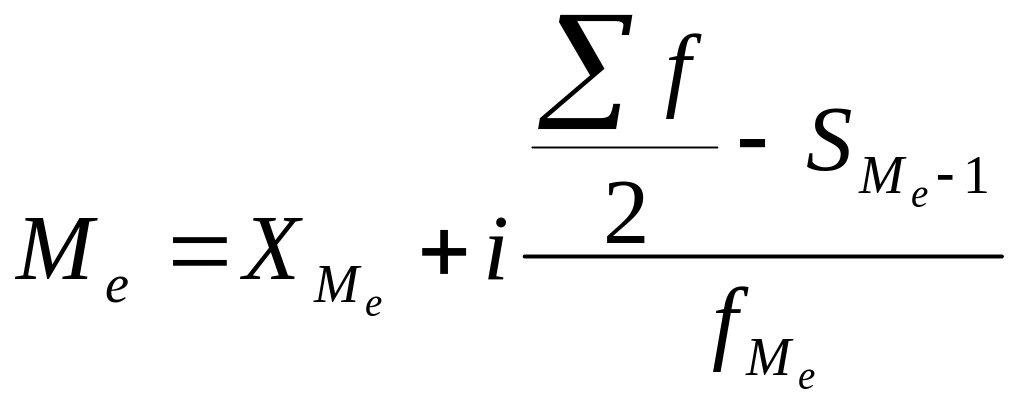де
– нижня
межа медіанного інтервалу; і
– величина медіанного інтервалу;
– частота медіанного інтервалу;
– сума нагромаджених частот домедіанного
інтервалу.
Для розв’язання п’ятої
задачі потрібно
засвоїти тему «Вибіркове спостереження»
[26, 242–268]. Гранична помилка вибірки для
середньої (
):
а) для повторної вибірки:
;
б) для безповторної вибірки:
,
де t
– коефіцієнт довір’я
при певній ймовірності;
– чисельність вибіркової сукупності;
– чисельність генеральної сукупності.
Межі генеральної середньої:
,
де
– середня у вибірковій
сукупності;
– середня у генеральній
сукупності.
Гранична помилка вибірки для
частки (
)
розраховується:
а) для повторного відбору:
;
б) для безповторного відбору:
,
де
– дисперсія альтернативної
ознаки;
де
– кількість одиниць, яким
притаманна певна властивість або ознака.
Межі генеральної частки:
,
де
– вибіркова частка;
– генеральна частка.
В кінці задачі студент робить висновок.
Для розв’язання шостої задачі потрібно опрацювати тему «Ряди динаміки» [26, 168–221].
Аналізуючи ряд динаміки, визначають:
1. Абсолютні прирости, темпи зростання і приросту базисні й ланцюгові, абсолютний вміст 1 % приросту [6, 238–242].
1.1
Абсолютні прирости (
):
а)
базисні
;
б)
ланцюгові
,
де
– поточний
рівень ряду;
– перший
рівень ряду;
–
попередній рівень ряду.
1.2.
Темпи зростання (
):
а)
базисні
;
б)
ланцюгові
.
1.3.
Темпи приросту (
):
а)
базисні
;
б)
ланцюгові
.
1.4. Абсолютний вміст 1 % приросту (А):
,
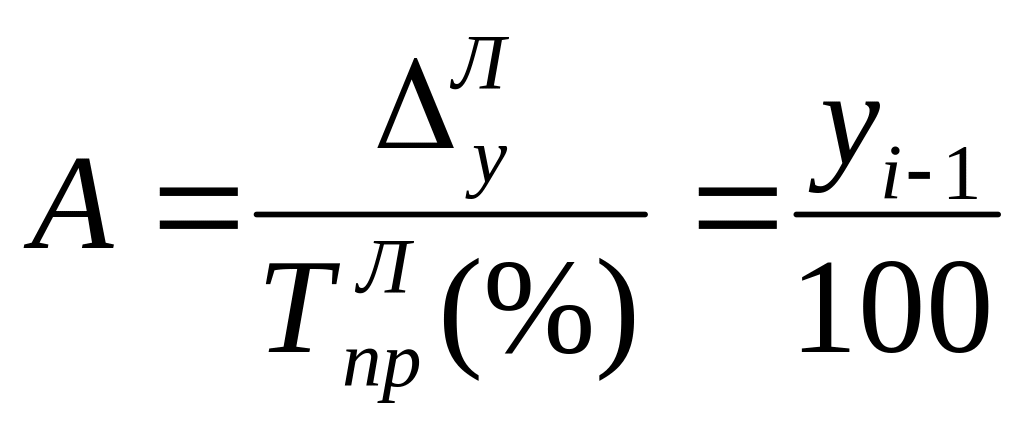де
– ланцюгові
темпи приросту, розраховані у процентах.
2. Середній рівень динамічного
ряду (
)
з однаковими інтервалами розраховують
за формулою середньої арифметичної
простої:
,
де
– сума рівнів ряду;
– кількість рівнів ряду.
3. Середній абсолютний приріст
(
)
розраховується за формулами:
,
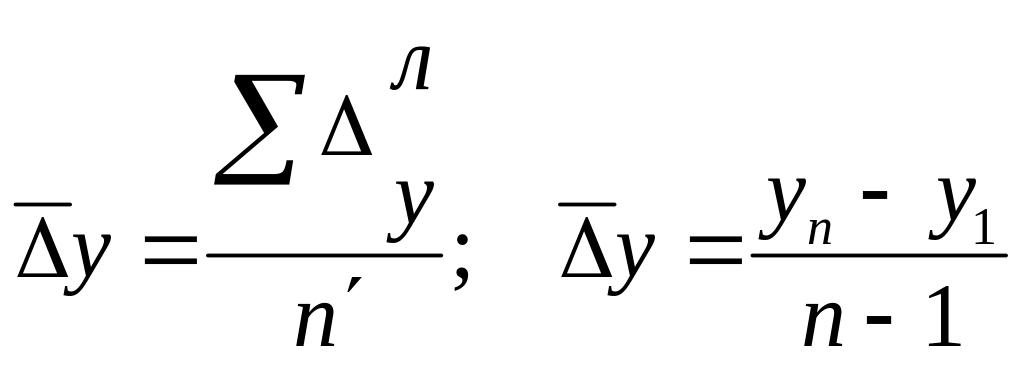де
– сума абсолютних ланцюгових приростів,
– кількість абсолютних ланцюгових
приростів;
– відповідно кінцевий і початковий
рівні ряду,
– кількість рівнів ряду.
4. Середньорічний коефіцієнт
зростання (
)
розраховується за формулами:
,
або
,
де
– ланцюгові коефіцієнти зростання;
– кількість рівнів ряду;
– кількість ланцюгових коефіцієнтів
зростання.
Середньорічний коефіцієнт приросту розраховується за формулою:
.
Після розрахунків необхідно, дотримуючись необхідних вимог, побудувати графік динамічного ряду [26, 46–73] та зробити висновок.
Для розв’язання задач 7–9 потрібно ретельно опрацювати тему «Індекси» [26, 222–241].
Задачу 7 розв’язують з використанням формул для розрахунку індивідуальних і загальних індексів. Наприклад:
,
де
– індивідуальні індекси відповідно
ціни, фізичного обсягу і собівартості
продукції;
– ціна одиниці продукції у базисному
та звітному періодах;
– кількість продукції у базисному і
звітному періодах;
– собівартість одиниці продукції у
базисному та звітному періодах.
Загальний (агрегатний) індекс цін (Ір) визначають за формулою:
,
де
– індексована величина;
– вага.
Загальний індекс фізичного
обсягу (
)
розраховується:
,
де
– індексована величина;
– вага.
Загальний індекс товарообороту
(
)
розраховується:
.
Взаємозв’язок названих індексів має наступний вигляд:
.
Абсолютний
загальний розмір зміни товарообороту
(
)
розраховується наступним чином:
,
в тому числі за рахунок зміни:
а)
цін:
;
б)
фізичного обсягу:
.
Між даними показниками існує взаємозв’язок:
.
Аналогічно
розраховується абсолютний розмір зміни
витрат на виробництво продукції (
).
В залежності від умови задачі 8 використовують формули для розрахунку середніх індексів:
а) середній арифметичний індекс фізичного обсягу:
;
б) середній гармонічний індекс цін або собівартості:
.
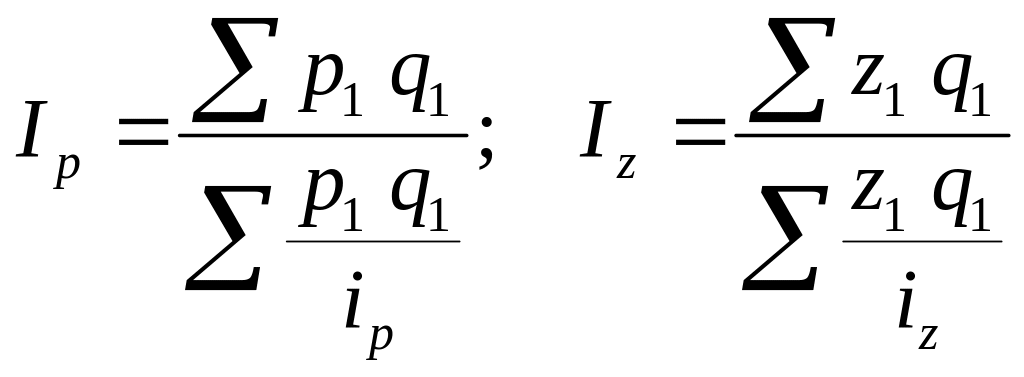У кінці задачі необхідно подати економічний висновок.
Для розв’язання задачі 9 розраховують наступні індекси:
а) індекс собівартості змінного складу:
;
б) індекс собівартості постійного (фіксованого) складу:
;
в) індекс структурних зрушень:
.
Між даними індексами існує відповідний взаємозв’язок:
.
Індекси ціни змінного, постійного складу та структурних зрушень розраховуються аналогічно. У кінці задачі необхідно подати економічний висновок.
Для розв’язання задачі 10 потрібно засвоїти матеріал теми «Статистичні методи вивчення взаємозв’язку» [26, 127–167].
Емпіричне кореляційне
відношення (
)
розраховується за формулою:
,
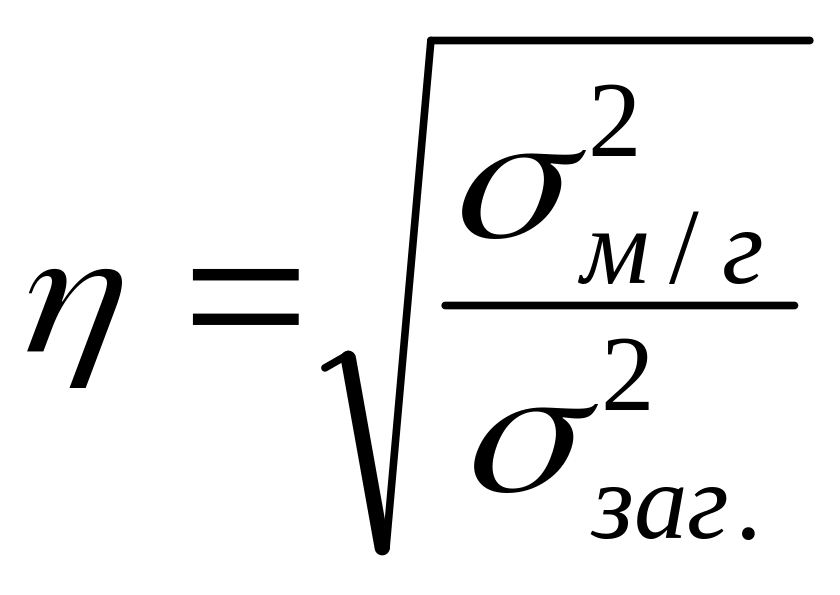де
– міжгрупова дисперсія, яка розраховується
за формулою:
– загальна дисперсія, яка
розраховується за формулою:
де
– групова середня;
– загальна середня для всієї
сукупності;
– кількість одиниць у кожній
групі;
– середня з квадратів значень
у.
Коефіцієнт детермінації (D) розраховується за формулою:
Для визначення сили та напряму зв’язку при лінійній кореляційній залежності використовують рівняння прямої та лінійний коефіцієнт кореляції.
Рівняння прямої має вигляд:
,
де
– вирівняне значення
результативної ознаки;
– факторна ознака;
– параметри рівняння.
Параметри рівняння визначають способом найменших квадратів, розв’язуючи систему рівнянь:
де – кількість значень х та у.
Параметри рівняння розраховуються наступним чином:
;
.
Лінійний коефіцієнт кореляції має вигляд:
де
– середні значення факторної
і результативної ознаки;
– середня з добутку ху;
– середнє квадратичне відхилення ознаки
х, яке
розраховується:
;
– середнє квадратичне відхилення ознаки
у, яке
розраховується:
,
де
;
.
Після розрахунку значення коефіцієнта кореляції будується графік прямої за значеннями х та з дотриманням вимог побудови статистичних графіків та робиться висновок про існування, силу і напрямок зв’язку між факторною і результативною ознаками.
При виконанні індивідуальних завдань студент має дотримуватися таких вимог:
1. Умови задач слід наводити повністю.
2. Розв’язування задач необхідно ілюструвати формулами, розрахунками, поясненнями.
3. Відносні величини, індекси розраховувати з точністю до 0,001, а інші показники – до 0,1.
4. В кінці кожного завдання повинен міститися ґрунтовний економічний висновок.
ВАРІАНТИ КОМПЛЕКСНИХ ПРАКТИЧНИХ
ІНДИВІДУАЛЬНИХ ЗАВДАНЬ
ВАРІАНТ ПЕРШИЙ
(виконують студенти, порядковий номер яких за списком 1, 11, 21, 31)
Задача 1
Є наступні дані про роботу 25–ти підприємств:
Таблиця 1
Підприємство |
Вартість основних засобів, млн. грн. |
Доход (виручка) від реалізації продукції, млн. грн. |
1 |
35 |
25 |
2 |
40 |
28 |
3 |
10 |
16 |
4 |
70 |
129 |
5 |
45 |
56 |
6 |
49 |
44 |
7 |
23 |
28 |
8 |
55 |
94 |
9 |
66 |
119 |
10 |
20 |
25 |
11 |
47 |
35 |
12 |
27 |
23 |
13 |
30 |
32 |
14 |
61 |
96 |
15 |
20 |
15 |
16 |
39 |
42 |
17 |
38 |
44 |
18 |
33 |
43 |
19 |
30 |
14 |
20 |
31 |
30 |
21 |
31 |
32 |
22 |
45 |
79 |
23 |
38 |
39 |
24 |
56 |
89 |
25 |
90 |
153 |
Для вивчення залежності між вартістю основних засобів і доходом згрупуйте підприємства за факторною ознакою, утворивши чотири групи з однаковими інтервалами. По кожній групі і по сукупності визначте:
1. Кількість підприємств.
2. Вартість основних засобів – усього і в середньому на одне підприємство.
3. Доход – всього і в середньому на одне підприємство.
Результати подайте у груповій таблиці.
Зробіть висновок.