
Линейная алгебра f1
1.Определители 2 и 3 порядков
Квадратной матрицей размерности 2 на 2 называется таблица состоящая из 4 чисел расположенных в 2х строках и 2х столбцах вида:(матрица)
В общем виде элементы матрицы можно записать в виде aij где - номер строки, j - номер столбца.
Определителем соответствующий данной квадратичной матрице 2 п-ка н-тся число, кот обозначается ∆ и находится по правилу a11*a22-a12*a21
Квадратной матрицей размерности 3на3 н-тся таблица состоящая из 9 чисел расположенных в 3х строках и 3х столбцах вида:(матрица)
Определителем матрицы 3го порядка называется число находящиеся по правилу разложения по первой строке.
2.Миноры и алгебраические дополнения. Разложение определителя по элементам строки или столбца. f2
Минором эл-та определителя 3го п-ка н-тся определитель 2го порядка полученный из определителя 3го п-ка путем вычеркивание строки и столбца на пересечении к-ых стоит данный э-нт.
∆=a11*M11-a12*M12+a13*M13
Алгебраическим дополнением э-та aij называется произведение его минора на (-1) в степени i+j.
∆=a11*А11+a12*А12+a13*А13
Правило: Определитель 3го порядка равен сумме произведений элементов любой строки или столбца на их алгебраическое дополнение.
3.Свойства определителей: f3
если строки определителя заменить его же столбцами, то определитель не изменится.
если 2 строки или 2 столбца поменять местами то определитель изменит знак на противоположный сохраняя абсолютное значение.
общий множитель эл-тов столбца или строки можно вынести за знак определителя.
если определитель содержит 2 одинаковых столбца или строки, то такой определитель равен 0.
если определитель содержит 2 пропорциональные строки или столбца, то такой определитель равен 0.
если определитель содержит строку или столбец полностью состоящий из 0 то такой определитель равен 0
если к элементам строки или столбца определителя прибавить элементы другой строки или столбца умноженных на одно и то же число то определитель не измениться.
Системы линейных уравнений. Основная и расширенная матрица. Критерии совместности системы. f4
Системой m линейных алгебраических уравнений с n-неизвестным называется следующая система:
{a11*x1+a12*x2+...a1n*xn=b1
a21*x1+a22*x2+...a2n*xn=b2
…………….
am1*x1+am2*x2+....amn*xn=bm}
где аi-коэффициент при неизвестных, bi-свободный член
Если все bi = 0 то система н-тся однородной.
Решением системы явл. такая совокупность xj* которая при подстановке xj* вместо xj в каждое уравнение системы обращает уравнения системы в тождество.
Система наз-тся совместной,если она имеет решение,и обратно.Однородная система всегда совместная тк она имеет нулевое решение.
Опр.:Совместная система называется определенной если она имеет единственное решение или не определенной если решений бесконечное множество.
2 системы называются равносильными если имеют одинаковые решения.
Система переходит в равносильную,если провести элементарные преобразования:
поменять 2 уравнения местами
любое уравнение системы умножить на не нулевое число.
любое уравнение системы умножить на число и прибавить к другому уравнению
Основная матрица системы называется матрица состоящая из коэффициентов и неизвестных
Расширенная матрица - матрица состоящая из коэффициентов, неизвестных и свободных членов
Строка a1 ,a2,…, an н-тся линейно зависимой если существуют такие числа α1, α2, αn что их сумма квадратов не равна 0, а сумма произведений на α1а1+α2 а2+…+αn аn равна 0.
Ранг - это максимальное количество линейно независимых строк.
Теорема Кронеккера-Капелли: Система совместна тогда и только тогда когда ранг матрицы равен рангу расширенной матрицы.
rgA=rg(A/B)
5.Метод Гаусса решения систем линейных уравнений f5
Если а11≠0, первую строку матрицы умножаем на (-а21/а11) и прибавляем ко второй строке матрицы. также с остальными.
Случаи:
если последняя строки имеет вид (0000…./bi), система не имеет решений.
При решении системы последнюю строку мы получаем в виде:(0 0…arr* arn*/br*) где r<n, следовательно система имеет множество решений.
r=n (0..ann*/bn*) ann*×xn=bn*
6.Формулы Крамера f6
Решение системы линейных алгебраических уравнений при ∆ ≠ 0 единственно и находится по формуле xi=∆i/ ∆, где ∆-определитель основной матрицы системы, а ∆i получается из дельта заменой i-того столбца на столбец свободных членов.
7.Системы однородных линейных уравнений f7
СЛУ называется однородной если все свободные члены всех уравнений=0. Система имеет хотя бы одно решение которое называется тривиальным или нулевым.
Если число у-ний системы = числу неизвестных, а определитель основной матрицы∆=0, то система имеет единственное тривиальное решение. Если ∆≠0, то система имеет множество решений.
Также если имеется не нулевое решение x1=c1 x2=c2..xn=cn, то для любого k ͼ R, что x1=k*c1 xn=k*cn.
Чаще всего однородные системы решаются методом Гаусса.
Матрицы. Действия над матрицами. f8
Прямоугольной матрицей размерности m на n н-ся матрица вида
(a11 a12 a1n
a21 a22 a2n
am1 am2 amn)
Действия над матрицами:
сравнение
2 матрицы одинаковы только тогда когда равны их соответствующие элементы
сложение
Суммой матриц одинаковой размерности называется матрица той же размерности элементы которой определяются по правилу cij=aij+bij
3)умножение на число
Умножением матрицы на число называется матрица той же размерности элементы которой определяются по правилу: каждый элемент умножается на это число.
произведение матриц
Произведение матрицы m на p на матрицу p на n называется матрица m на n полученная по правилу cij=aij*bij+ai2*B2j+aip*bpj
обратная матрица
Единичной матрицей называется квадратная матрица по главной диагонали которой стоят 1 а остальные 0.
Опр.:Матрица А-1n на n называется обратной матрицы А m×n если произведение матрицы А-1 × А=Е (единичной матрице)
Теорема: Для того чтоб квадратная матрица имела обратную необходимо и достаточно чтобы она была не вырождена те ее определитель был отличен от 0, тогда обратная матрица определяется по правилу
A-1 = ( A11/∆ A12/дельта A1n/дельта
A21/дельта A22/дельта A2n/дельта
Am1/дельта Am2/дельта Amn/дельта где А - это алгебраическое дополнение соответствующих элементов.
Векторы и линейные операции над ними. f9
Вектор - отрезок имеющий длинну и направление.
Длинна вектора - его модуль.|АВ|=|а|
Колинеарные - 2 параллельных вектора сонапр и противополнапр.
Комланарные - 3 вектора параллельные одной плоскости.
2 вектора равны др др если они 1)сонапрвлены, 2)коллинеарны, 3)имеют одинаковые длины.
Операции над векторами:
сложение (если др за др -треугольник, если из одной точки - параллелограмм)
сумма векторов подчиняется переместительному з-ну а+в=в+а и сочинительномуз-ну (а+в)+с=а+(в+с)
2) вычитание (если из одно точки - треугольник)
умножение вектора на число
Результатом умножения является вектор длинна которого равна произведению модуля числа k на длину вектора а и если к>0 сонаправлен а, а если к<0 то противоположнонаправлен.
Базис на плоскости и в пространстве. f10
Базисом на плоскости или в пространстве называется максимальное число линейно независимых векторов.
На плоскости базисом являются 2 неколлинеарных вектора. В пространстве базисом являются 3 некомпланарных вектора.
Опр.:Линейная комбинация векторов а1 а2 аn - сумма вида α1*a1+ α2*a2... где αi вещественное число.
Система векторов а1 а2 аn н-тся линейно зависимой если существуют такие числа α 1 α2 не все равные 0, что линейная комбинация равна 0. Если же линейная комбинация равна 0 только когда все α = 0, такая система называется линейно независимой.
Теорема 1: Любые 2 коллинеарных вектора линейно зависимы.
Док-во: а||b тогда по свойству умножения вектора на число можно найти такое число х чтобы а=x*b тогда a-xb=0 получили линейную комбинацию α1=1 α2=-х
один коэффициент ≠0, поэтому линейно зависима.
Следствие 1: Любые 2 неколлинеарных вектора линейно независимы.
Теорема 2: Пусть векторы a и b неколлинеарны тогда любой компланарный вектор c можно представить единственным образом в виде линейной комбинации.
Док-во: пусть a не|| b, проведем с из точки пересечения a и b и продолжим их. Из конца с проведем прямые || a и b. ОС=с=ОВ+ОА
ОВ||b подбираем х OB=x*b
OA||a подбираем у OA=y*a
с=хb+ya
Пусть существую другие числа x1 y1 с=х1b+y1a не равные x y
Вычтем из равенства 1 равенство 2
0=(x-x1)b+(y-y1)a
Получили что линейная комбинация a и b =0. Но тк они линейно независимы это возможно только когда оба коэффициента равны 0. x=x1 y=y1
Следствие 1: Любые 3 компланарных вектора линейно зависимы
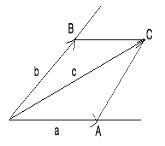 Следствие
2: Любые 3 некомпланарных вектора линейно
независимы.
Следствие
2: Любые 3 некомпланарных вектора линейно
независимы.
Теорема 3: Пусть 3 вектора a b c некомпланарны, тогда любой вектор d в пространстве можно единственным образом представить в виде линейной комбинации.
d=xa+yb+zc
Следствие: Любые 4 вектора в пространстве линейно зависимы.
11. Проекция вектора на ось и ее свойства. f11
Осью называется направленная прямая.
Проекцией точки А на ось l называется точка А’ полученная опусканием перпендикуляра из А на l.
Проекцией вектора АВ на ось l называется длинна отрезка А’B’ где А’ - проекция т. А на ось l, а В’ проекция точки В, взятая с положительным знаком если направление вектора совпадает с направление оси.
Свойства проекции:
постоянный множитель выносится за знак проекции
Проекция суммы векторов равна сумме проекций
прlа=lal*cos φ
Прямоугольная система координат. Координаты вектора и точки. f12
Прямоугольной системой координат называется совокупность точки О называемой центром и ортонормированного базиса векторов i j k. i j k взаимно перпендикулярны и имеют длину=1.
Продолжения i j k называются координатными осями. i - ось абсцисс, j - ось ординат, k - ось аппликат.
Координаты точки М - это координаты ее радиус вектора.
Пусть даны координаты точек А (xa, ya, za) B (xb, yb, zb). АВ можно представить в виде разности векторов OB-OA следовательно координатами вектора AB {xb-xa, yb-ya, zb-za}
Вектор а состовляет с осями координат углы α, β, γ и эту углы находятся по формулам cos α,β,γ= ax,y,z/lal
Скалярное произведение векторов. f13
Скалярным произведение называется число равное произведению их длин на косинус угла между ними. a*b=lal*lbl*cos φ
Свойства:
Подчиняется переместительному закону
Подчин-ся распределительный закон (a+b)*c=a*c+c*b
закон коммутативности (λa)*(Mb)=(λM)*(a*b)
скаляр произведение вектора на себя равно квадрату его длины.
признак перпендикулярности: a*b=0,когда a перпендикулярно b
разложение по единичным векторам
a {ax, ay, az} a=axi+ayj+azk a*b=ax*bx+ay*by+az*bz
14.Векторное произведение векторов. f14
Векторным произведением 2х векторов а и b называется вектор с удовлетворяющий 3 условиям:
вектор с перпендикулярно а и b
длинна вектора с численно равна площади параллелограмма построенный на векторах а и b как на сторонах. lcl=lal*lbl*sinφ
вектора а b и с образуют правильную 3ку векторов
Свойства:
переместительный з-н не действует а×b= -b×а
распределительный закон (a+b)×c=a×c+b×c
закон коммутативности (λa)×(Mb)=(λM)*(a×b)
признак коллинеарности векторов
a×b=0 a и b колинеарны. а×а=0
вычисление векторного произведения
a×b= (i j k
ax ay az
bx by bz)
i j k i j вправо с + влево с –
Смешенное произведение векторов f15
Смешенным произведением называется сложное произведение при котором 2 вектора перемножаются векторно а результат умножается на 3й вектор скалярно.
abc=(a x b)*c= lax ay az
bx by bz
cx cy czl
Свойства:
abc=-bac
если любые 2 вектора колинеарны или равны друг другу, произведение равно 0
закон коммутативности (λа)(μb)(γc)=(λμγ)abc
(a+b)cd=acd+bcd
Геометрический смысл смешенного произведения
Построим вектора a b c с началом в одной точке. a x b=d достроим пралепипет на a b c.
abc=(a x b)*c=la x bl*c*cos φ=S*прdc=Sh
V=labcl
признак комплонарности векторов
abc=0
Общее уравнение прямой на плоскости f16
Прямой на плоскости называют геометрическое место точек на плоскости, координаты которых удовлетворяют линейному уравнению относительно текущих координат х у.
Ах+Ву+С=0
Частные случаи:
С=0 проходит через начало координат
А=0 параллельно абсциссе(х)
В=0 параллельно ординате(у)
А=С=0 абсцисса(х)
В=С=0 ордината(у)
17.Уравнения прямой с угловым коэффициентом, в отрезках на осях f17
у=kx+b
k-угловой коэффициент, числено равный тангенсу угла который прямая составляет с положительным направлением абсциссы.
b-это отрезок который прямая отсекает от начала координат.
x/a+y/b=1уравнение прямой в отрезках
x/(-C/A)+y/(-C/B)=1
a b отрезки которые прямая отсекает на абсциссе и ординате.
18. Уравнение прямой на плоскости( проходящей через данную точку, через 2 точки) f18
Пучек- это совокупность всех прямых кототрые можно провести через точку на плоскости.
y-y0=k(x-x0) уравнение прямой, проходящей через точку
(x-x1)/(x2-x1)=(y-y1)/(y2-y1) уравнение прямой проходящей через 2 точки
19.Угол между прямыми на плоскости. Условия параллельности и перпендикулярности прямых. f19
φ=α2-α1
tgφ=tg α2-tg α1=(tg α2 - tg α1)/(1+tg α2 * tg α1)
tg α2 = k2
tg α1 = k1
tg φ = (k2-k1)/(1+k1×k2)
Усл.|| и ┴
ℓ1: y=k1x+b1
ℓ2: y=k2x+b2
1)ℓ1//ℓ2 φ=0 tg φ=0 (k2-k1)/(1+k1*k2)=0 k1=k2
2)ℓ1┴ℓ2 φ=90 ctg φ=0 (1+k1*k2)/(k2-k1)=0 1+k1*k2=0 k1= - 1/k2
Расстояние от точки до прямой на плоскости f20
ℓ:Аx+By+C=0 M(x0,y0)
 Расстояние
от точки до прямой определяется длина
перпендикуляра опущенным из точки на
прямую
Расстояние
от точки до прямой определяется длина
перпендикуляра опущенным из точки на
прямую
d=lA*x0+B*y0+cl/√(A^2+B^2)
Если число стоящее под знаком модуля больше 0 то точка лежит выше прямой, если меньше, то ниже, если равна 0, то на прямой.
Уравнение плоскости в пространстве(проходящей через данную точку,через две точки) f21
Плоскостью называется множество точек пространства координаты, которых удовлетворяют линейному уравнению относительно текущих координат х у z вида:
Ax+By+Cz+D=0
Частные случаи:
D=0 ,О ͼ α
A=0 ,α//OX
B=0 ,α//OY
C=0 ,α//OZ
A=B=0 , α//XOY
A=C=0 ,αXOZ
B=C=0 ,α//YOZ
A=D=0 ,пл-ть проходит ч/з координатную ось Ох Охͼα
B=D=0 ,αͼОУ
C=D=0 ,αͼОZ
A=B=D=0 ,XOY
A=C=D=0 ,XOZ
B=C=D=0 ,YOZ
A(x-x0)+B(y-y0)+C(z-z0)=0 Уравнение плоскости проходящей через точку и нормальный вектор
x/(-D/A)+y/(-D/B)+z/(-D/C)=1 уравнение плоскости в отрезках
l x-x1 y-y1 z-z1
x2-x1 y2-y1 z2-z1 - уравнение плоскости проходящей через 3 точки
x3-x1 y3-y1 z3-z1l
Угол между плоскостями. Условия параллельности и перпендикулярности плоскостей. f22
cos(α1^α2)=N1*N2/lN1l*lN2l
Условие параллельности:
α1//α2=> N1//N2=> A1/A2=B1/B2=C1/C2=m
если D1=D2=m,тогда плоскости совпадают
Условие перпендикулярности:
α1 ┴ α2 =>N1 ┴ N2 =>N1*N2=0
А1*А2+В1*В2+С1*С2=0
Расстояние от точки до плоскости. f23
Пусть дана пл-ть α1:
Ах+Ву+Сz+D=0 и М0(x0,y0,z0)
За расстояние от точки до плоскости примем длину перпендикуляра опущенного из точки к плоскости.
Возьмем на плоскости произвольную т-ку М1(x1,y1,z1),т.к. она лежит на пл-ти, то ее коор-ты удовлетворяют. Аx+By+Cz+D=0. Образуем М1М0{x0-x,y0-y,z0-z}его проекция на норм вектор N взятая по абсолютному значению, это и есть искомая величина d
d=|N*M1M0 / |N||
d=lAx0+By0+Cz0+Dl/√(A2+B2+C2)
Общие уравнения прямой в пространстве. f24
Прямой в пространстве называется линия пересечения 2х плоскостей поэтому задается системой уравнений пересекающихся плоскостей.
{А1х+В1у+С1z+D1=0
А2х+В2у+С2z+D2=0
25.Векторные и параметрические уравнения прямой в пространстве. f25
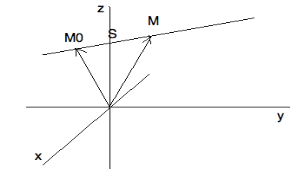
Прямая в пространстве определяется точкой лежащей на прямой и вектором параллельным этой прямой или лежащий на ней. Вектор S называется направляющим вектором прямой.
Возьмем произвольную точку М(x,y,z)
М0М=ОМ-ОМ0 => ОМ=ОМ0+М0М
S//L
можно найти t при котором M0M=t*S
OM=r OM0=r0
r=r0+ts векторное уравнение
Координаты радиус вектора точки совпадает с координатами точки
{x=x0+t*m
y=y0+t*n - параметрические уравнения прямой
z=z0+t*p
Канонические уравнения прямой в пространстве. Уравнение прямой проходящей через 2 точки. f26
1)t=(x-x0)/m=(y-y0)/n=(z-z0)/p x-x0/m=y-y0/n=z-z0/p - канонические ур-я прямой
Зам 1: Если хотя бы одна из координат направляющего вектора равна 0, это значит что прямая перпендикулярна соответствующей оси.
Зам 2: Для того чтобы от общих ур-ний прямой перейти к каноническим или параметрическим,необходимо определить т-ки прямой (одна координата задается, остальные находятся из системы)и направляющий вектор
2)Если даны 2 точки, образуем вектор, который лежит на прямой и является направляющим. Каноническое уравнение: (x-x1)/(x2-х1)=(y-y1)/(y2-y1)=(z-z1)/(z2-z1)
Угол между двумя прямыми в пространстве. Условия параллельности и перпендикулярности прямых. f27
За угол м/у прямыми в пространстве принимается один из 2-х смежных углов м/у прямыми проходящими ч/з 1 т-ку ||-ых данных прямых
Угол можно найти как угол между направляющими векторами этих прямых.
cos (ℓ1^ℓ2)=cos(S1^S2)=S1*S2/lS1l*lS2l
Условия параллельности:
ℓ1//ℓ2 S1//S2 m1/m2=n1/n2=p1/p2
Условия перпендикулярности
ℓ1 ┴ ℓ2 S1 ┴ S2 S1*S2=0
Угол между прямой и плоскостью. f28
За угол между прямой и плоскостью в пространстве принимается угол между прямой и ее проекцией на плоскость
cos φ= lN*Sl / lNl*lSl
Условие параллельности:
α // ℓ => S ┴ N => S*N=0
Условие перпендикулярности:
α ┴ ℓ => S//N => m/A=n/B=p/C
Точка пересечения прямой и плоскости. f29
Пусть дана пл-ть α: Аx+By+Cz+D=0 и прямая {x=x0+t*m
y= y0+t*n
z=z0+t*p
А(x0+t*m)+B(y0+t*n)+C(z0+t*p)+D=0 и находим значения параметра t:
t=(D-Ax0-By0-Cz0)/(Am+Bn+Cp)
и t подставляем в параметрическое уравнение прямой.
Кривые второго порядка. Окружность. f30
1)Кривой второго порядка называется множество точек пл-тей координаты которых удовлетворяют уравнению 2го порядка относительно текущих координат х у. Вида:
Ax2+2Bxy+Cy2+2Dx+2Ey+F=0 При чем ABC одновременно не могут равняться 0.
2)Окружностью называется геометрическое место точек равноудалённых от фиксированной точки пл-ти называемой центром окр-ти. Радиус - расстояние от точек окружности до его центра.
(x-a)2+(y+b)2=R2
Эллипс. f31
Эллипсом называют геометрическое место точек пл-ти сумма расстояний от каждой из которых до 2х фиксированных точек называемых фокусами, является величиной постоянной и больше чем расстояния между фокусами.
x2/a2+ y2/b2=1 -каноническое ур-е эллипса b2=a2-c2
A1(-a;0) A2(a;0) B1(0;b) B2(0;-b)
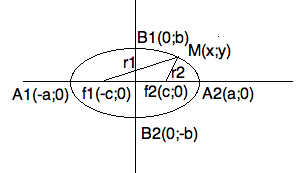 2a-
большая
осью
a- большая
полуось
2a-
большая
осью
a- большая
полуось
2b- малая ось b- малая полуось
Формулу эллипса характеризует эксцентриситет.
E=c/a<1 чем ближе он к 1 тем вытянутее эллипс по оси ОХ
Расстояние от точек до фокусов - фокальный радиус
r1=a+E*x r2=a-E*x
Гипербола f32
 Гиперболой
называется геометрическое место точек
в плоскости абсолютная величина
разностей
расстояний
от каждой из которых до 2х фиксированных
точек
называемых фокусами есть величина
постоянная
и меньше расстояния
между
фокусами.
Гиперболой
называется геометрическое место точек
в плоскости абсолютная величина
разностей
расстояний
от каждой из которых до 2х фиксированных
точек
называемых фокусами есть величина
постоянная
и меньше расстояния
между
фокусами.
x2/a2-y2/b2=1 b2=c2-a2
2a- действительная ось a- действительная полуось
2b- мнимая ось b -мнимая полуось
r1=la+E*xl r2=la-E*xl
Парабола f33
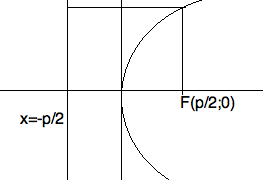
Параболой называется геометрическое место точек пл-ти равноудалённых от фиксированной т-ки пл-ти называемый фокусом и фиксированной прямой на пл-ти называемой директрисой .
 Возможны
след. случаи
Возможны
след. случаи
2px=y2 p параметр >0
y2=-2px ветви направлены влево
x2=2py вверх
x2=-2py вниз
Преобразование координат. Параллельный перенос осей. f34
В системе координат возьмем xOy точку О’(a,b), проведем через нее оси O’X’ O’Y’ // OX OY. Совокупность этих точек дает новую систему координат.
Возьмем точку М (х;у) в ХОУ а в ‘X’O’Y’ (x’;y’).
x’=x-a – новые координаты через старые
y’=y-b
35. Полярная система координат. Ее связь с прямоугольной системой. f35
Полярной системой координат называется совокупность точки О называемой полюсом и оси P называемой полярной осью.
Каждой точке соответствуют 2 числа r и φ, где r - это полярный радиус, расстояние от точки до полюса, а φ - угол который луч ОМ образует с положительным направлением полярной оси. Если φ положительный, то откладывается против часовой стрелки, если отрицательный - по часовой стрелке. М(φ;r)
Совмещаем полюс с началом координат и полярную ось с абсциссой.
M(x;y) (φ;r)
r2=x2+y2 φ=arctg y/x =arcsin y/√r=arccos x/√r
y=r*sinφ x=r*cosφ
36.Предел функции в точке. f36
Число b называется пределом функции f(x) при x->а если для любого E>0 существует такое δ зависящее от (E)>0 что из неравенства 0<lx-al<δ => |f(x)-b|<E
limx->af(x)=b
Из определения следует что когда х изменяется от а-δ до а+δ график функции находится на полосе между у=в-Е и у=в+Е
Бесконечно малые и бесконечно большие функции. f37
Функция вида f(x) называет Б м при x->a если для любого Е>0 существует δ зависящее от (Е)>0,такое что из нер-ва 0<lx-al<δ следует |f(x)|<E
Функция вида f(x) наз-ся б.б,при x->a, если для любого L>0 существует δ>0,такое что из нер-ва 0<lx-al<δ следует |f(x)|>L
Теорема 1: Функция обратная к бм при x->a является бб и наоборот.
Док-во: f(x) бм x->a для любого хͼ(a-δ,а+δ) |f(x)|<E. На том же самом интервале если поменять функцию на обратную меняется знак.
l1/f(x)l>1/E 1/E=L l1/f(x)l>L
Функция f(x) наз-ся ограниченной на множестве М если существует С>0 такое что для любого x ͼ М |f(x)|<=C
Если f(x) имеет предел при x->a, то она ограничена в некоторой окрестности точки а.
Теорема 2: При произведении бм функции f(x) при x->a на ограниченную функцию g(x) есть функция бм.
Следствие 1: Произведение 2х бм функций при х->а есть бм функция.
Следствие 2: Произведение постоянного множителя на бм есть бм.
Теорема 3: Сумма 2х бм функций есть бм функция.
Теорема 4: Отношение f(x) бм при x->а ,к функции к функции предел которой отличен от 0, есть функция бм.
38. Основные теоремы о пределах.(предел постоянной, связь ф-ции с ее пределом, предел суммы) f38
Теорема 1: предел постоянной равен самой постоянной.
Limx->ac=c lf(x)-bl<E lc-cl=0<E
Теорема 2 (о связи функции с пределом): Для того чтобы b=lim f(x) при x->a необходимо и достаточно чтобы f(x)=b+α(х)
Док-во: lim x->a f(x)=b l f(x)-b l<E f(x)=b+α(х)
lα(х)l<E α(х) -бм
α(х)=f(x)-b
lim x->a f(x)=b
Теорема 3: Предел суммы конечного числа функций имеющие пределы lim x->a (f(x)+g(x))=lim x->a f(x)+lim x->a g(x) равен сумме их пределов.
39.Основные теоремы о пределах(предел произведения, предел частного, предел промежуточной ф-ции) f39
Теорема 4: Предел произведения конечного числа функций имеющих пределы при x->a равен произведению lim x->a f(x)*g(x)=lim x->a f(x)*lim x->a g(x)
Док-во: lim x->a f(x)=b f(x)=b+α(х)
Lim x->a g(x)=c g(x)=c+β(х)
f(x)*g(x)=(b+α(х))*(c+β)=b*c - бм
Следствие: Постоянный множитель можно выносить за знак придела.
Теорема 5: Предел отношения 2х ф-ций имеющие предел при x->a равен отношению их пределов при условии что предел знаменателя отличен от 0.
Lim x->af(x)/g(x)=lim x->a f(x)/lim x->a g(x) ; lim x->a g(x)≠0
Теорема 6: (лемма о 2х полицейских): Если функции f(x), g(x), φ(x) удовлетворяет неравенству f(x)<=g(x)<=φ(x) в некоторой окрестности точки а и f(x) и φ(x) имеют равные пределы то и функция имеет такой же предел в окрестности этой точки.
40.Первый замечательный предел. f40
Первый
замечательный предел
имеет вид:

Второй замечательный предел. f41
Последовательностью называется функция заданная на множестве натуральных чисел.
Возрастающая последовательность - это последовательность в которой каждый ее последующий элемент больше предыдущего. Последовательность называется ограниченной если существует такое число с>0 что модуль каждого члена последовательности <=c
Теорема: Всякая возврастающая ограниченная последовательность имеет предел.
limx->∞(1+1/x)^x= limx->∞(1+x)^1/x=e
e=2,7
Понятие о неопределённостях. Общие приемы раскрытия неопределенностей. f42
Часто для вычисления пределов существуют такие ситуации вида {0/0};{ ∞/∞}, {1∞}, {+- ∞}; {∞∞}называемые неопределенностями.
Примеры раскрытия неопределенностей:
∞/∞ делим на старшую степень
∞ - ∞ к общем знаменателю
корень-корень бесконечность - бесконечность домножаем на корень+корень
бесконечность + бесконечность= +бесконечность
Сравнение бм функций. Эквивалентность бм. f43
1)Пусть α (х) и β (х) – бм x->a, тогда имеют место соотношения:
α (х) и β (х) называются бм одного порядка малости если предел их отношения равен числу отличеному от нуля.
α (х) имеет более высокий порядок малость если lim x->a α (х)/β (х)=0
α(х) имеет более низкий порядок малости если lim x->a α(х)/β(х)=∞
α(х) имеет порядок малости к относительно β(х) если lim x->a α(х)/β(х) =А(≠0;≠∞)
бм называются не сравнимыми если предела их отношения lim x->a α(х)/β(х) не существует.
2)2 бм при x->a называются эквивалентными если lim x->a f(x)/g(x)=1
Если f(x) эквивалентно g(x) то существует их примерное равенство при x->a
Теорема 1: Пусть f(x) эквивалентен f1(x), а g(x) эквивалентен g1(x), тогда если существует lim x->a f(x)/g(x), то существует и lim x->a f1(x)/g1(x) и эти пределы равны.
Док-во:
lim x->a f(x)/g(x)= lim x->a f1(x)/g1(x) * f(x)/f1(x) * g1(x)/g(x) = lim x->a f1(x)/g1(x) * lim x->a f(x)/f1(x) * lim x->a g1(x)/g(x) = lim x->a f1(x)/g1(x)
Теорема 2: Для того чтобы f1(x) эквивалентна g1(x) достаточно чтобы их разность была бм более высокого порядка.
Док-во: пусть f(x) эквивалентен g(x)
lim x->a β(х)/g(x)=lim x->a (f(x)-g(x))/f(x)=lim x->a f(x)/f(x)-lim x->a g(x)/f(x)= 1-1=0
Пусть β(х) бм
lim x->a β(х)/f(x)=0 lim x->a (f(x)-g(x))/f(x)=0 lim x->a f(x)/f(x)-lim x->a g(x)/f(x)=0 1-lim x->a g(x)/f(x)=0 lim x->a g(x)/f(x)=1
Теорема 3: Сумма конечного числа бм эквивалентен слагаемому имеющий самый низкий порядок малости.
Основные эквивалентности:
sin α (х) эквивалентно α(х)
tg α(х) эквивалентноα(х)
arcsin α (х) эквивалентно α(х)
arctg α(х) эквивалентно α(х)
e α(х) -1 эквивалентно α(х)
ln(α(х)+1) эквивалентно α(х)
a α(х) -1 эквивалентно α(х)*lna
Непрерывность функции в точке. Классификация точек разрыва. f44
1)Функция f(x) непрерывна в точке x=x0 если:
f(x) определена в некоторой окрестности точки х0
существует предел f(x) при x->x0
limx->x0 f(x)=f(x0)
Если в точке х0 существует односторонний предел равный значению функции в этой точке, то если этот предел слева и он равен х0 то говорят о непрерывности функции справа.
Если точка х0 принадлежит к области определения, нарушается хотя бы одно из условий непрерывности то точка х0 называется точкой разрыва.
2)Если в точке х0 существует конечные односторонние пределы, то х0 называется точкой разрыва 1го рода, причем если lim x->x0+0 f(x)=lim x->x0-0 f(x) ≠ f(x0) то х0 называется точкой устранимого разрыва.
Если односторонние пределы конечно не равны друг другу, то говорят что в этой точке функция терпит скачек.
Если хотя бы один из односторонних пределов равен бесконечности, х0 называется точкой разрыва второго рода.
Непрерывность элементарных функций. Действия над непрерывными функциями. f45
Теорема 1: Пусть функции f(x) и g(x) непрерывны в точке х0 тогда их сумма и произведение также непрерывны в этой точке, если g(x0)≠0 то отношение этих функций также непрерывно в этой точке х0.
Док-во: F(x)=f(x)*g(x) непр lim x->x0F(x)= lim x->x0 f(x)*g(x)=lim x->x0 f(x) * lim x->x0 g(x)=f(x0)*g(x0)=F(x0)
Все осн. Элементарные ф-ции непрерыв.в области их определения
Теорема 2: Пусть u=φ(х) непрерывна в х0, а y=f(u) непрерывна в u0=φ(х0), тогда y=f(φ(х)) непрерывна в х0.
Свойства функции, непрерывных на отрезке. f46
Функция f(x) называется непрерывной на отрезке [a,b] если она непрерывна в каждой ее внутренней точке, а на концах в точке а непрерывна справа, а в точке b непрерывна слева.
lim x->а+0f(x)=f(a) lim x->b-0 f(x)=f(b)
Теорема 1: Если функция непрерывна на отрезке [a,b] то на этом отрезке она достигает своего наибольшего и наименьшего значения.
Если отрезок заменить интервалом, то теорема становится неверна.
Следствие: Если функция непрерывна на отрезке, то она ограничена на этом отрезке.
Теорема 2: Если функция f(x) непрерывна на [a,b] и на концах отрезка принимает значения с разными знаками, то существует хотя бы одна точка принадлежащая отрезку, в которой функция равно 0.
Теорема 3: f(x) непрерывная на [a,b] принимает значения на его концах А и В тогда какое бы ни было число С лежащие между А и В, существует как минимум 1 число С на [a,b] что f(c)=C.
Определение производной. Ее геометрический и физический смысл. f47
Производной функции f(x) в точке х0 называется предел отношения приращения функции в этой точке к приращению аргумента при произвольном стремлении последнего к 0.
lim∆ х->0 ∆ y/∆ х=lim ∆ х->0 (f(x0+ ∆ х)-f(x0))/∆ х=f’(x0)
Физический смысл:
S=f(t) дельта t =t-t0
средняя скорость находится V= дельтаS/дельтаt
дельта t->0 тогда можно найти мгновенную скорость V(t0)=lim дельта t->0 дельта s/ дельта t=S’(t0)
Производные основных элементарных функций. f48
(c)’=0
(xn)’=n*xn-1
(ex)’=ex
(ax)’=ax*lna
(ln x)’=1/x
(logax)’=1/xlna
(cosx)’= - sinx
(sinx)’=cosx
(tgx)’=1/cos2x
(ctgx)’=-1/sin2x
(arcsinx)’=1/√(1-x2)
(arccosx)’=-1/√(1-x2)
(arctgx)’=1/1+x2
(arcctgx)’= - 1/1+x2
Основные правила дифференцирования. f49
Теорема 1: Если функции f(x) и g(x) дифференцируема в точке х то их сумма также дифференцируется в этой точке и ее производная равна (f(x)+g(x))’=f’(x)+g’(x)
Теорема 2: Если f(x) g(x) дифференцируема в точке х то их произведение также дифференцируется в этой точке и ее производная находится по правилу (f(x)*g(x))’= f’(x)*g(x)+g’(x)*f(x)
Док-во: F(x)=f(x)*g(x)
F(x+∆x)=(f(x)+∆f(x))*(g(x)+∆g(x))
∆f=f(x+∆x) -f(x)
∆f+f(x)=f(x+∆x)
∆g=g(x+∆x)-g(x)
∆g+g(x)=g(x+∆x)
F(x+∆x)=f*g+∆f*g+f*∆g+∆f*∆g
∆F=F(x-∆x)-F(x)=∆f*g+f*∆g+∆g*∆f
F lim∆x->0 ∆f/∆x=lim ∆x->0 ∆f*g/∆x+lim ∆x->0 ∆g*f/∆x+lim∆x->0 ∆g*∆f/∆x=g*lim ∆x->0 ∆f/∆x+f*lim∆x->0 ∆g/∆x+lim ∆x->0 ∆ f* lim∆x->0 ∆g/∆x=g*f’+f*g’
Следствие: Постоянный множитель выносится за знак производной.
Теорема 3: Если функции f(x) и g(x) дифференцируемы в точке х то и их части также дифференцируема в этой точке и его производная находится по правилу (f/g)’=(f’*g-g’*f)/g2 при условии что в точке х функция g≠0.
Дифференцируемость функции и ее связь с непрерывностью. f50
Если функция имеет производную в точке то она называется дифференцируемой в этой точке.
Если функция имеет производную в каждой точке некоторого интервала, то она называется дифференцируемой на этом интервале.
Теорема 1: Если функция дифференцируема в точке х0, то она непрерывная в этой точке.
Док-во: ∆x=x-x0 ∆y=f(x)-f(x0)
рассмотрим предел приращения функции ∆y=∆y/∆x * ∆x
lim∆x->0 ∆y=lim∆x->0 ∆y/∆x*∆x=lim∆x->0 ∆y/∆x * lim∆x->0 ∆x=f’(x)*0=0
lim∆x->0 f(x)-f(x0)=0
lim∆x->0 f(x)= lim∆x->0f(x0)
Производная сложной функции. f51
Теорема: Пусть функция u=φ(х) дифференцирована в точке х и имеет производную u’x, а функция y=f(u) дифференцируемая в точке u имеет производную y’u, тогда сложной функция y=f(φ(х)) дифференцируема в точке х, то производная определяется по правилу yx’=y’u*u’x
Док-во: Предадим х приращение ∆х, u=f(x) получится приращение ∆u, а y=f(u) получит приращение ∆у. ∆u≠0
∆y/∆x=∆y/∆u=∆u/∆x
lim∆x->0 ∆y/∆x=lim ∆ x->0 ∆y/∆u * ∆u/∆x=lim ∆ x->0 ∆y/∆u * lim ∆ x->0 ∆u/∆x
в силу непрерывности если ∆u->0 то и ∆x->0
=lim ∆ u->0 ∆ y/∆u * lim ∆x->0 ∆u/∆x=y’u*u’x
Производная обратной функции. f52
Пусть функция y=f(x) возрастает или убывает на отрезке [a,b]. х пробегает значения от а до с, y пробегает значение от b до d. Существует функция x=f(y) которая каждым значениям у из интервала от c до d ставит соответствующий х из интервала от a до b. Обратная функция.
Теорема: Пусть функция x=φ(y) является обратной функцией y=f(x) и имеет производную в точке у равную φ’(y) тогда функция f(x) будет дифференцируема в соответствующей точке х и ее производная будет равна f’(x)=1/φ’(y)
Док-во:
x= φ(y) придадим аргументы приращение ∆у,тогда ф-ция получит приращение ∆х
lim ∆ y->0 ∆x/∆y=lim ∆ y->01/∆y/∆x={ ∆x->0}=lim ∆ x->01/ lim ∆x->0 ∆y/∆x=1/lim ∆ x->0 ∆y/∆x=1/f’(x)
Логарифмическое дифференцирование. Дифференцирование неявных функций. f53
y=[f(x)]g(x)
lny=g(x)*ln f(x)
y’/y=g’(x)*ln f(x) + g(x)* f’(x)/f(x)
y’=[f(x)]g(x)(g(x)*ln f(x)+g(x)*f’(x)/f(x))
Неявной называется функция представленная в виде равенства содержащая х и у и неразрешимая относительно х. Чтобы дифференцировать ее, дифференцируют обе стороны от х помня что у - функция от х, а затем выражают у’
Производные высших порядков. Физически смысл второй производной. f54
1)2ой производной называется производная от ее 1й производной.
f’’(x)=(f’(x))’
Производной n-ого порядка называется производная от ее n-1 производной.
f(n)(x)=(f(n-1)(x))’
2)Физический смысл: Пусть точка движется прямолинейно и ее скорость меняется по закону v=f(t)
(V(t+∆t)-V(t))/∆t=ωср (среднее ускорение на данном участке)
∆t->0 значит мгновенной ускорение:
ω(t)=lim(V(t+ ∆t)-V(t))/∆t=V’(t)
тк скорость производная пути: ω(t)=(S’(t))’=S’’(t)
Дифференциал функции. f55
f’(x)= ∆x называется главной частью приращения функции, линейной относительно приращения аргумента или ее дифференциалом и обозначается dy(df(x))
dy(x)=f’(x)∆x
Рассмотрим y=x dx=(x’)*∆x=1*∆x=∆x
df(x)=f’(x)*dx
Дифференциал суммы, произведения, частного. Дифференциал сложной функции. f56
1)d(f(x)+g(x))=df(x)+dg(x)
Док-во: d(f(x)+g(x))=(f(x)+g(x))’dx=(f(x)+g’(x))dx=f’(x)dx+g’(x)dx=df(x)+dg(x)
Дифференциал произведения определяется по правилу d(f*g)=gdf+fdg
d(f/g)=(gdf-fdg)/g2
Следствие 1: dcf(x)=cdf(x)
Следствие 2: df(x)=d(f(x)+c)
2)y=f(x) x=φ(х) y=f(φ(t))
dy=y’t dt=y’x*x’t dt=y’xdx
Инвариантность формы дифференциала: Форма дифференциала не меняется от того является ли переменная независимой или промежуточной.
Дифференциал высших порядков. Применение дифференциала к приближенным вычислениям. f57
1)Дифференциалом n-го порядка равен диф-лу от диф-ла n-1 порядка и определяется формулой
dn(y)=f(n)*(x)dxn
2)∆y=f’(x) ∆x
dy= ∆y
f(x0+ ∆x)=f(x0)+f’(x0) ∆x
Дифференцирование ф-ций,заданных параметрически f58
Функция может задаваться неявным образом y=f(x),а как совокупность 2х функций x=φ(t) y=x(t) зависящих от 3- ей переменной t, который называется параметром. t пробегает все значения из совместной области определения функций.
y=ψ(t) x=φ(t) => t=Ф(х)
y=ψ(Ф(х)) y’x=ψ’t* Ф’х y’x=ψ’t / φ’t y’’x=(ψ’x)t’ / φ’t
Теорема Ферма. f59
Пусть функция f(x) определена и непрерывна на (а,в) и достигает на этом интервале своего наибольшего или наименьшего значения в некоторой точке, тогда если в этой точке существует производная ф-ции, она =0.
Доказательство: Пусть в точке с принадлежащей (а,в) функция принимает наибольшее значение, тогда для любого ∆х f(c+∆х)-f(c)≤0
Теорема Ролля f60
Пусть функция f(x) определена и непрерывна на [a,b] и дифференцирована во всех его внутренних точках и принимает в его концах значение равное 0, тогда существует точка с ͼ [a,b] что f’(c)=0
Док-во: По свойствам функции непрерывных на отрезке, f(x) достигает своего наименьшего и наибольшего значения, значит согласно теорема Ферма, производная функции равна 0.
Замечание: На концах a и b, функция может не равняться 0, а просто иметь одинаковые значения.
Геометрический смысл: Существует точка на отрезке (a,b), в которой касательная // ОХ.
61.Теорема Лагранжа. f61
Пусть функция f(x) определена и непрерывна на отрезке (а,в) и дифференцирована во всех его внутренних точках, тогда существует точка с принадлежащая (а,в) что имеет место равенство (f(b)-f(a))/b-a=f’(c)
Док-во: A(a,f(a)) B(b,f(b)) (y-f(a))/(f(b)-f(a))=(x-a)/(b-a)
y=f(a)+(f(b)-(f(a)/(b-a))*(x-a)
f(x) равна разности ординат точек с абсциссой х.
F(x)=f(x)-f(a)-(f(b)-(f(a))/(b-a)(*x-a)
Функция удовлетворяет всем условиям теоремы Ролля. F(b)=0
Функция дифференцированная на отрезке (а,в) F’(x)=f’(x)-(f(b)-f(a))/(b-a)
Согласна теорема Ролля существует точка с что F’(c)=0
f’(c)=(f(b)-f(a))/(b-a)
Геометрический смысл: f’(c)-угловой коэффициент точки с. (f(b)-f(a))/(b-a) угловой коэффициент секущей. При выполнении условий теоремы, существует точка в которой касательная // секущей.
