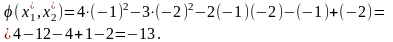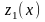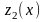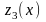Вопросы для самопроверки

Как называется универсальный метод решения задач линейного программирования и в чем его суть?

Что позволяет выявление недефицитных ограничений в задаче об использовании ресурсов?

К чему приводят изменения исходных данных статической задачи планирования производства?

Что определяют коэффициенты прямых материальных производственных затрат?

Что показывают коэффициенты полных материальных затрат?

Как из матрицы коэффициентов прямых материальных производственных затрат можно получить матрицу коэффициентов полных материальных затрат и наоборот?

Когда для решения задач математического программирования применяется метод динамического программирования?

Чем отличаются задачи условной оптимизации от задач безусловной оптимизации?

Что отражает целевая функция в задаче об использовании ресурсов (оптимального планирования производства)?

Что отражает целевая функция в задаче оптимального распределения валовых капитальных вложений?

Что представляет собой оптимальное решение задачи условной оптимизации и экстремальное решение задачи безусловной оптимизации?

Что определяют ограничения задачи условной оптимизации?

Каким методом можно свести задачу условной оптимизации к такой задаче безусловной оптимизации, чтобы оптимальные решения этих задач совпадали?

Примеры решения задач

1. Найти экстремум функции

.

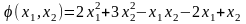Решение.

Необходимые условия экстремума:

,

.

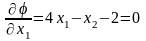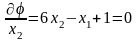Из системы уравнений

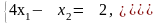
находим .

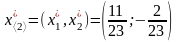Достаточные условия экстремума:

,

.

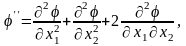
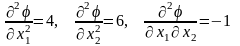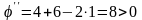Следовательно, в точке 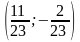функция имеет минимум:

.

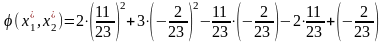2. Для изготовления 2-х видов продукции используются 3 типа ресурсов.

Запасы ресурсов и их расход на изготовление продукции, а также прибыль, получаемая от реализации одной единицы продукции, приведены в таблице:

Тип ресурса	Запас ресурса	Число единиц ресурсов, затрачиваемых на изготовление одной единицы продукции
		1-й вид продукции	2-й вид продукции
1-й тип	2	0,04	1
2-й тип	4	0,5	2
3-й тип	6	1	3
Прибыль от реализации единицы продукции		35	16

Требуется построить математическую модель задачи линейного программирования для составления такого плана производства продукции, при котором прибыль от ее реализации будет максимальной.

Решение.

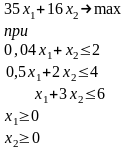
3. По данным отчетного периода получен следующий баланс трехотраслевой экономической системы:

№ отраслей		Потребители			Конечная продукция	Валовая продукция
		1	2	3
1 2 3		20	40	30	110	200
		30	16	60	54	160
		10	24	16	150	200

Определить валовый выпуск отраслей, обеспечивающий новый конечный продукт .

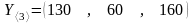Решение.

Расчет коэффициентов прямых затрат: ,

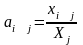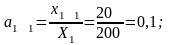
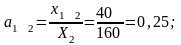
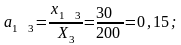
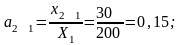
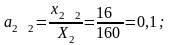
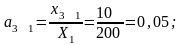
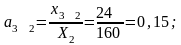
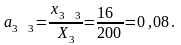
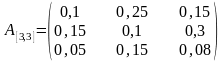
Расчет коэффициентов полных затрат:

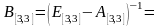
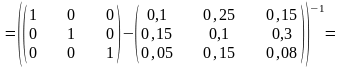
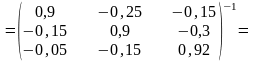
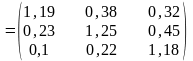¹

Определение валового выпуска отраслей:

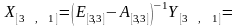
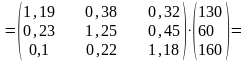
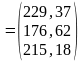
4. Для реконструкции трех заводов выделено 5 млн. руб. капиталовложений. Увеличение выпуска продукции (в млн. руб.) после реконструкции в зависимости от выделенного -ому заводу 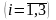объема капиталовложений 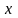обозначим 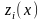и зададим в таблице:

1	5	7	6
2	12	10	13
3	16	14	18
4	21	20	21
5	23	25	22

Необходимо найти вариант распределения капиталовложений, при котором суммарное увеличение выпуска продукции на трех заводах максимально.

Решение.

Сначала (прямой прогон) рассчитаем функции, показывающие суммарное увеличение выпуска продукции на заводах, по рекуррентному соотношению:

.

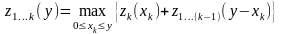Для 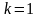, т.е. при выделении объема капиталовложений одному заводу (например, первому) функция совпадает с .

Рассчитаем функцию :

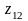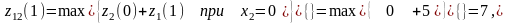
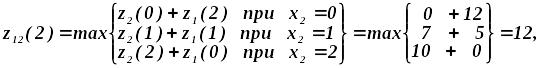
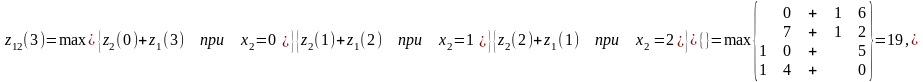
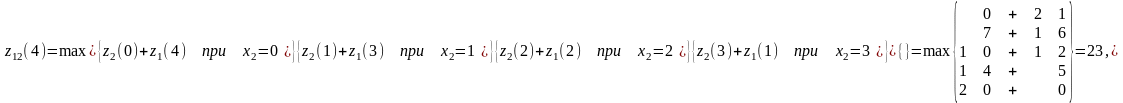
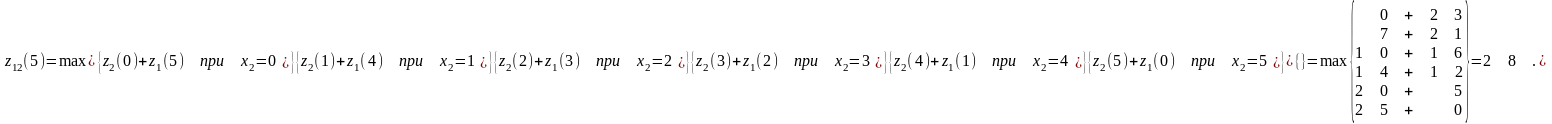
Рассчитаем функцию 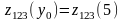, т.к. только при полном выделении капиталовложений всем заводам достигается максимальное суммарное увеличение выпуска ими продукции:

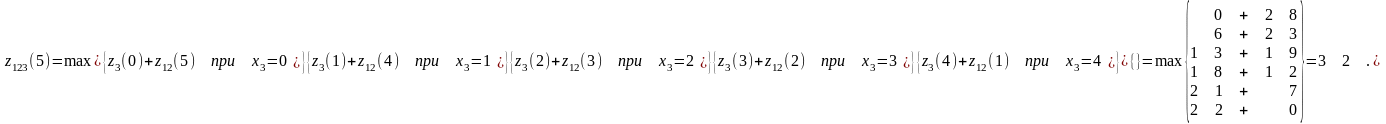
Затем (обратный прогон) находим, что максимальное суммарное увеличение выпуска продукции не трех заводах 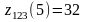млн. руб. При этом третьему заводу выделяется 2 млн. руб. капиталовложений, а остальным двум – 3 млн. руб.

При выделении двум оставшимся заводам 3 млн. руб. капиталовложений максимальное суммарное увеличение выпуска продукции на них 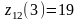млн. руб. При этом второму заводу выделяется 1 млн. руб. Тогда первому заводу выделяется оставшиеся 2 млн. руб. капиталовложений.

Итак, максимальное суммарное увеличение выпуска продукции на трех заводах 32 млн. руб. при оптимальном распределении капиталовложений 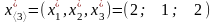млн. руб.

5. Найти условный экстремум функции

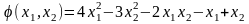
при условии (ограничении)

.

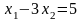Решение.

Составим функцию Лангранжа:

.

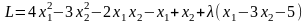Необходимые условия экстремума:

,

,

.

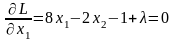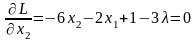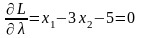Из системы уравнений

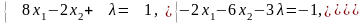
находим

.

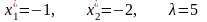Достаточные условия экстремума:

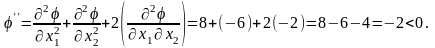
Следовательно, в точке 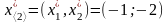целевая функция 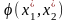имеет максимум: