1. Модели оптимизации в экономике
1.1. Задача об использовании ресурсов (оптимального планирования производства)
Будем рассматривать статическую задачу планирования, в которой параметры остаются неизменными на всем плановом периоде.
Пусть конечный
продукт
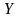как часть валового продукта
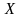состоит из
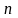видов продукции (номенклатура продукции).
Целью увеличения объема конечного
продукта, а следовательно, и валового
продукта выберем максимизацию дохода
(выручки) от реализации этой продукции.
Если
-
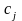доход (выручка, цена) от реализации
единицы продукции
-ого
вида (
).
Тогда, если планируется выпустить
единиц продукции
-ого
вида, то суммарный доход по всем видам
продукции будет выражаться величиной:
.
Отсюда целевая функция примет вид:
.
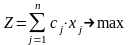Объем выпускаемой
продукции зависит от используемых
ресурсов и основных производственных
фондов (ОПФ). Поэтому, если для производства
используются
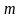видов ресурсов и их затраты для выпуска
единицы продукции определяются ОПФ,
то можно ввести следующие обозначения:
-
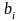имеющийся запас (резерв)
-ого
вида ресурсов;
-
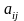количества единиц, или объем
-ого
вида ресурсов, затрачиваемой, или
расходуемый на выпуск одной единицы
-ого
вида продукции.
Тогда объем выпускаемой продукции зависит от следующих ограничений:
,
.
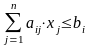Доход от
реализации выпускаемой продукции
зависит от спроса на нее. Обозначим
объем спроса на продукцию
-ого
вида через число единиц продукции этого
вида
.
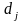Тогда ограничения по спросу примут
вид:
,
.
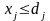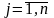Следует оговориться, что данные о спросе на продукцию прогнозируются или определяются полученными заказами. Если спрос превышает предложение, то соответствующие ограничения могут отсутствовать.
Наконец, введем стандартные ограничения на неотрицательность переменных, имеющие ясный прикладной смысл:
,
.
Таким образом, задача об использовании ресурсов сформулирована полностью и имеет общий вид:
при ограничениях
, ;
, ;
, .
Эта задача относится к задачам линейного программирования и решается универсальным симплекс-методом (Приложение 1). Оптимальное решение задачи позволяет провести анализ его на чувствительность к изменениям исходных условий, т.е. выявить недефицитные ограничения, что может позволить уменьшить запас имеющихся ресурсов, а следовательно, снизить расходы на их приобретение и хранение.
Однако некоторые непредвиденные изменения исходных данных такой статической задачи в ходе планового периода могут привести к тому, что полученное оптимальное решение - оптимальный план окажется нереализуемым и потребуется его корректировка.
1.2. Задача определения объема выпуска валовой продукции
Будем рассматривать валовый продукт как единое целое без разделения его на виды продукции. Вместе с тем будем учитывать, какая отрасль (предприятие, цех) выпускает этот продукт. Тогда весь валовый продукт может быть представлен вектором в матричном виде:
,
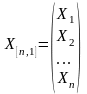где
-
стоимость валового продукта, выпускаемого
-ой
отраслью,
.
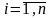Для выпуска
-ой
отраслью валового продукта
ей нужно воспользоваться в качестве
производственного потребления частью
валового продукта
,
выпущенного как ей самой (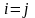
),
так и другими отраслями (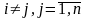
).
Размер такой части
определяется с помощью коэффициента
прямых затрат
(коэффициент прямых материальных
производственных затрат):
,
где показывает стоимость части продукции -ой отрасли, непосредственно затрачиваемой в качестве предметов труда не выпуск единицы стоимости продукции -ой отрасли.
Коэффициенты прямых затрат могут быть сведены в матрицу:
.
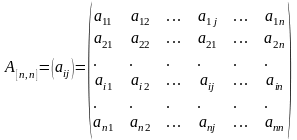Тогда балансовое соотношение может записано в следующем матричном виде:
.
Можно считать, что объем конечного продукта определяется заказами. Требуется найти, какой объем валового продукта обеспечит выполнение этих заказов.
Преобразования приведенного балансового соотношения приводят к выражению валового продукта через конечный продукт :
,
,
,
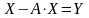где
- единичная матрица.
Получена новая матрица коэффициентов в виде обратной матрицы:
.
Эта матрица
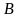называется матрицей коэффициентов
полных затрат, или обратной матрицей
Леонтьева. Коэффициент полных материальных
затрат
показывает потребность в валовом
выпуске продукции
-
ой отрасли для производства единицы
конечной продукции
-ой
отрасли.