Приложение 2. Планирование центром оптимального распределения капитальных вложений между предприятиями методом динамического программирования

Метод ДП может быть использован как для динамических, так и для статических систем. Здесь приведен пример использования метода ДП для оптимального распределения ресурсов, то есть для решения статической оптимизационной задачи. Смысл этой задачи состоит в следующем: центр должен так распределить имеющиеся у него капитальные вложения между своими предприятиями, чтобы суммарная отдача от этих вложений для центра была максимальной.

Целевая функция центра при этом имеет следующий вид:

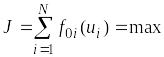(П.2.1)

где функция f_0i характеризует эффективность (отдачу) капитальных вложений u_i в i-ое предприятие для центра, N - число предприятий.

Типичная зависимость функций f_0i(u_i) приведена на рис П.2.1.

Рис. П.2.1. Типичная зависимость эффективности

капитальных вложений

Зависимости f_0i(u_i), приведенные на рис. П.2.1, можно аппроксимировать экспонентой или параболой. Возьмем последнюю как более простую функцию вида:

,

где A_i, B_i - известные центру коэффициенты аппроксимирующих функций, A_i > 0, B_i > 0. Известен также суммарный объем капитальных вложений подлежащий распределению между предприятиями, u_i - доля капитальных вложений в i - ое предприятие.

Для постановки задачи в классическом виде введем новую целевую функцию:

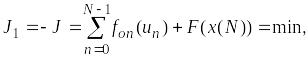(П.2.2)

где n = i - 1 – новая нумерация предприятий от нуля до N - 1,

n = 0 ¸ N - 1.

Для описания процесса распределения ресурсов между предприятиями введем разностное уравнение вида:

x(n + 1) = x(n) + u(n), n = 0 ¸ N - 1, (П.2.3)

где x - сумма распределенного капитала,

u - доля капитала, выделенная n-ому предприятию.

Задано ограничение на долю капитала в виде u(n) ³ 0, начальное условие x(0) = 0.

При этом ограничение 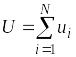примет следующий вид x(N) = U. Это означает, что в процессе распределения

надо так раздавать капиталы (ресурсы), чтобы после их раздачи у центра ничего не осталось. В противном случае, если все значения u(n) = 0, то весь капитал останется у центра, что противоречит условиям задачи. Эта ситуация должна быть наказана. Для этого терминальную функцию F(x(N)) зададим в виде:

(П.2.4)

где M - коэффициент штрафа центру, зададим его очень большим числом.

Тогда с учетом (П.2.2) и (П.2.4) получим:

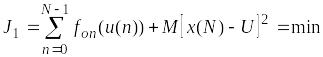. (П.2.5)

Эта целевая функция совместно с разностным уравнением (П.2.3) и заданными ограничениями ставит оптимизационную задачу планирования центру.

Решение. Для сформулированной задачи запишем уравнение Беллмана с краевым условием:

тогда ,

где u_оп(n, x) - оптимальное распределение ресурсов центра для n-ого предприятия.

Пусть число предприятий N = 3, суммарный ресурс капитальных вложений центра U = 10(млн. руб.), а функции f_0i заданы в виде:

f₀₁ = 16u - 0,4u²

f₀₂ = 18u - 0,6u² (П.2.6)

f₀₃ = 25u - 0,7u²

При новой нумерации предприятий от нуля до N - 1 = 2 с учетом (П.2.2) имеем:

f₀₀ = - f₀₁ = 0,4u² – 16u

f₀₁ = - f₀₂ = 0,6u² – 18u

f₀₂ = - f₀₃ = 0,7u² – 25u

Оптимальное решение задачи планирования будем искать методом ДП от второго предприятия к нулевому.

При n = 2 уравнение Беллмана:

а с учетом краевого условия j(3,x) = - M(x - u)² оно примет вид:

так как U = 10 , a f₀₂(u) = 0,7u² – 25u.

Поскольку число М >> 0, то для максимизации j оптимальное значение u_оп(2) должно обратить в нуль значение в круглых скобках, то есть (x + u_оп-10) =0, откуда u_оп(2) = 10 – x. При этом

При n = 1 получим следующее уравнение Беллмана:

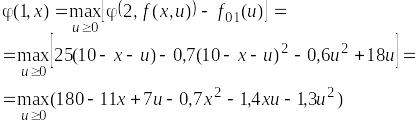
Возьмем от выражения в скобках производную по u и приравняем ее к нулю. В результате получим: 7 - 1,4x - 2,6u_оп = 0

или b - 2,6u_on = 0, где b = 7 - 1,4x.

На рис. П.2.2 построены прямые вида y = b – 2,6u_оп при различных значениях коэффициента b = 7 – 1,4x.

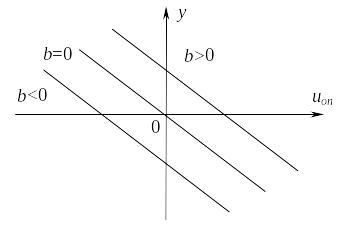
Рис. П.2.2. Прямые вида y = b – 2,6u_оп при

разных значениях коэффициента b

Так как по условиям задачи u ³ 0 , то оптимальное значение u_оп(1) будет определяться по выражению:

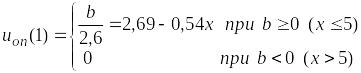
Подставим это значение u_оп(1) в выражение для j(1, x) и получим:

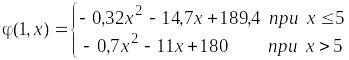
При n = 0 уравнение Беллмана примет вид: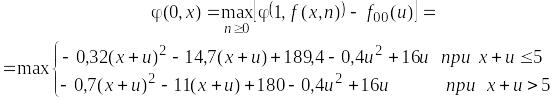

После раскрытия скобок и приведения подобных членов получим:

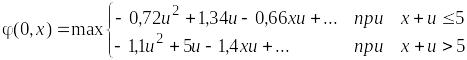
Здесь многоточие означает слагаемые, не зависящие от u.

Так как по условиям задачи u > 0, то неравенства x + u £ 5 и x + u > 5 приводят к условию 0 £ x £ 5.

Возьмем производную при x + u £ 5 и приравняем ее нулю. В результате получим: -1,44u + 1,34 - 0,66x = 0 или -1,44x + b = 0, где b = 1,34 - 0,66x.

По аналогии при n = 1 здесь получим значение оптимального управления

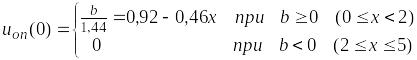
Теперь возьмем производную при x + u > 5 и приравняем ее нулю:

- 2,2u + 5 – 1,4x = 0 или - 2,2u + b = 0

где b = 5 – 1,4x, откуда

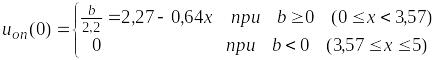
Так как мы получили два разных результата для u_оп(0), следовательно, эта задача имеет два оптимальных решения.

Приведем одно из этих решений для первого выражения

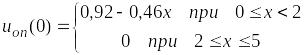
Так как x(0) = 0, то по этому выражению получим u_оп(0) = 0,92 (млн. руб.)

Тогда x(1) = x(0) + u_оп(0) = 0 + 0,92 = 0,92.

Для этого значения x определим u_оп(1) по соотношению, полученному при n = 1.

u_оп (1) = 2,69 – 0,54 ´ 0,92 = 2,19 (млн. руб.)

Тогда x(2) = x(1) + u_оп(1) = 0,92 + 2,19 = 3,11.

Для этого значения x определим u_оп(2) по соотношению, полученному при n = 2

u_оп(2) = 10 – 3,11 = 6,89 (млн. руб.).

Убедимся, что u_оп(0) + u_оп(1) + u_оп(2) = 0,92 + 2,19 + 6,89 = 10 (млн. руб.) = U.

В таблице П.2.1 приведены результаты расчетов функций f_0i и целевой функции центра J по приведенным выше формулам (П.2.6) и (П.2.2) при оптимальном планировании.

Таблица П.2.1

i	1	2	3
uоп(i)	0,92	2,19	6,89
f0i	14,38	36,54	138,86	J = 189,78

В таблице П.2.2 приведены результаты расчетов функций f_0i и целевой функции центра по формулам (13) и (8) при неоптимальном планировании, когда все получили поровну, то есть при (млн. руб.).

Таблица П.2.2

i	1	2	3
u(i)	3,333	3,333	3,333
f0i	48,84	53,28	75,48	J = 177,6

Из этой таблицы видно, что при неоптимальном планировании получили = 177,6 < 189,78.

Второе оптимальное решение поставленной задачи найдем при использовании второго выражения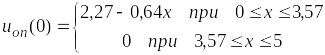

Так как x(0) = 0, то из этого выражения получим u_оп(0) = 2,27 (млн. руб.).

Тогда x(1) = x(0) + u_оп(0) = 2,27. Для этого значения x(1) получим u_оп(1) = = 2,69 – 0,54 ´ 2,27 = 1,464 (млн. руб.). Тогда x(2) = x(1) + u_оп(1) = 3,734.

Для этого значения x(2) получим:

u_оп(2) = 10 - 3,734 = 6,266 (млн. руб.).

Проверка: u_оп(0) + u_оп(1) + u_оп(2) = 10 (млн. руб.) = U.

Для этого варианта планирования значения функций f_0i и целевой функции центра J по формулам (П.2.6) и (П.2.1) приведены в таблице П.2.3. Из нее следует, что этот максимум меньше первого.

Таблица П.2.3

i	1	2	3
uоп(i)	2,27	1,464	6,266
f0i	34,26	25,066	129,166	J = 188,5

Если отдать весь капитал третьему предприятию, то есть u(1) = 0, u(2) = 0, а u(3) = 10 (млн. руб.), то целевая функция центра составит:

= f₀₃ = 25u(3) – 0,7u²(3) = 250 – 0,7 ´ 100 = 180 < 189,78.

Таким образом приведенные расчеты показывают, что только при оптимальном распределении капиталовложений между предприятиями целевая функция центра достигает своего максимального значения.