Задания для самостоятельной работы
1. Какое должно
быть непроизводственное потребление
на интервале времени
для того, чтобы рост валового продукта
определялся зависимостью
?
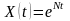2. Во
сколько раз увеличится непроизводственное
потребление
в
конечный момент времени
по сравнению с начальным моментом
времени
,
если рост валового продукта определяется
зависимостью
?
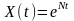3. Какие нужны
капитальные вложения
на интервале времени
для того, чтобы воспроизводство основных
производственных фондов (ОПФ) определялось
зависимостью
?
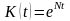4. Рассчитайте значение целевого функционала, определяющего качество изменения основных производственных фондов (ОПФ).
5.
Во сколько раз нужно увеличить капитальные
вложения
в конечный момент времени
по сравнению с начальным моментом
времени
для того, чтобы воспроизводство основных
производственных фондов (ОПФ) определялось
зависимостью
?
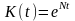6. Рассчитать значение
целевого функционала в задаче оптимального
управления развитием экономики на
интервале управления
при
.
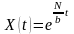7. Рассчитать значение
целевого функционала в задаче оптимального
управления распределением капитальных
вложений на интервале управления
при
.
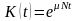8. Для роста валового
продукта, определяемого зависимостью
,
рассчитано, что непроизводственное
потребление, т.е. управление в задаче
оптимального управления развитием
экономики, должно быть
.
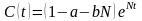Требуется определить, во сколько раз
нужно увеличить непроизводственное
потребление, т.е. изменить управление
в задаче оптимального управления
развитием экономики, для того, чтобы
рост валового продукта увеличился в
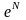раз.
9. Во сколько раз нужно
уменьшить валовые капитальные вложения
(инвестиции)
для того, чтобы основные производственные
фонды уменьшились с
до
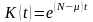в задаче оптимального управления
распределением капитальных вложений?
Заключение
В представленном учебном пособии рассмотрены теоретические основы теории оптимального управления, разобран ряд примеров экономических задач данного типа. Рассмотренные в пособии задачи иллюстрируют логику теории оптимального управления, не представляют вычислительных сложностей и допускают ручной счет. В то же время большинство реальных производственных задач являются объемными, что не могут быть решены в разумные сроки без применения вычислительных средств типа ЭВМ. Обозначенный «разрыв» между уровнями требуемых средств не должен создавать впечатление недостаточной «приспособленности» изученного метода для решения реальных задач; напротив, именно на объемных трудоемких задачах достоинства и преимущества передовых математических методов проявляются наиболее отчетливо.
В этой связи представляется целесообразным обучение студентов программным средствам, позволяющим решать подобные объемные задачи и в тоже время не требующие глубокого знания программирования и нюансов математических методов. Среди таких программных средств можно отметить табличный процессор Excel пакета Microsoft Office с настройкой «Поиск решения» или OpenOffice.org Calc. Такой подход в полной мере отвечает современным тенденциям математизации наук через посредство компьютерных технологий и позволяет эффективно сочетать устоявшиеся традиционные методы преподавания математики «с мелом у доски» с использованием современных программно-технических средств.
Высокая потенциальная эффективность математизации не реализуется самопроизвольно, а требует подготовки математически грамотных специалистов. Подчас даже неглубокой математической подготовки достаточно, чтобы понять, на каком направлении деятельности предприятия или организации могут быть полезны математические оценки, прогнозы и оптимизации. Напротив, недостаточный уровень подготовки и понимания возможностей математики может служить причиной отказа от применения математических методов даже в тех случаях, когда они заведомо позволят выявить скрытые резервы и дать значительный дополнительный экономический эффект.
Не подлежит сомнению, что изучение математики формирует системность и аналитичность мышления, исключительно важные для специалистов любых направлений. При этом важно показать, что математика не есть «абстрактное искусство», демонстрирующее излишнее усложнение действительности, - ее изучение позволяет овладеть мощными методами количественного анализа, имеющими широкие практические приложения. Данное положение во многом определяет отношение студентов-экономистов ко всему циклу математических дисциплин, одним из изящных разделов которого и является теория оптимально управления в экономике.