3.2. Модель развития экономики: магистральная теория
Исходя из соотношений поставленной выше задачи оптимального управления развитием экономики, уменьшение значения непроизводственного потребления способствует увеличению значения валового продукта . Однако низкий уровень непроизводственного потребления приводит к снижению прироста валового продукта . Это объясняется, например, недостаточностью подготовки трудовых ресурсов , которая способствует увеличению коэффициента приростной фондоемкости , и в итоге, неудовлетворительной эффективности валовых капитальных вложений .
Таким образом,
на определенном уровне развития
экономики существует некоторая
постоянная величина непроизводственного
потребления
,
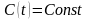обеспечивающая приемлемый прирост
валового продукта
,
и такое управление развитием экономики
в этом периоде времени близко к
оптимальному. Полученные соотношения
на данном периоде времени называются
магистралью.
Магистрали предшествует период времени и заканчивается она периодом времени, в которых величина непроизводственного потребления находится на низком уровне, что соответствует оптимальному управлению в эти периоды.
Сошлемся на образное представление сути магистрали и магистрального функционирования экономики [10], поясняющее это название. Допустим, что мы находимся в начальном пункте и нам нужно на автомобиле переехать в конечный пункт. Неподалеку от начального и конечного пунктов проходит автотрасса - аналог в данном случае магистрали. Мы оптимальным образом от начального пункта по местной дороге доезжаем до автотрассы, далее въезжаем на магистраль и едем по ней до местной дороги, ближайшей к конечному пункту, после чего съезжаем с магистрали и по местной дороге добираемся до конечного пункта. Эта интерпретация дает интуитивное представление об оптимальном развитии экономики.
3.3. Задача оптимального управления распределением валовых капитальных вложений
Вернемся к
рассмотрению производственно-технологической
схемы экономики (см. рис. 2.7). По этой
схеме рост ОПФ
происходит за счет валовых капитальных
вложений
(инвестиций). Причем часть этих инвестиций
представляет собой амортизационные
отчисления
:
,
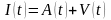где
,
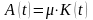- коэффициент амортизации.
А чистые
капитальные вложения
пропорциональны приросту ОПФ
:
.
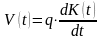Последнее соотношение учитывает естественную постепенность ввода в действие инвестиций. В совокупности все эти соотношения представляют следующую зависимость:
,
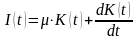или
.
Полученное дифференциальное уравнение описывает связь между ОПФ и инвестициями (валовыми капитальными вложениями) . Если теперь считать ОПФ состоянием, а валовые капитальные вложения - управлением, то можно сформулировать постановку задачи оптимального управления распределением валовых капитальных вложений.
Пусть интервал времени управления будет продолжительностью от начального момента времени по конечный момент времени .
Состояние описывается функцией ОПФ , а управление - функцией валовых капитальных вложений .
Тогда начальное
состояние представляет собой величину
,
а допустимое управление ограничивается
минимальной
и максимальной
величинами возможных валовых капитальных
вложений
:
.
В качестве уравнения движения (связь состояния - ОПФ и управления - валовых капитальных вложений ) будем использовать выведенное выше соотношение:
.
Целевой функционал (целевая функция от функции управления и от функции состояния) представим в виде:
,
где и - весовые коэффициенты, , устанавливающие приоритеты требований, составляющих цель управления.
Экономический смысл представленного целевого функционала раскрывается при рассмотрении следующих крайних случаев:
- при
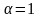и
целевой функционал отражает минимизацию
суммарного (интеграл) расходования
инвестиций, т.е. максимально экономного
распределения валовых капитальных
вложений;
- при
и
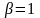целевой функционал (его терминальный
член) выражает стремление максимизировать
величину ОПФ к концу периода управления.
Таким образом, в целевом функционале заложены два противоположных требования, служащих одной и той же цели - оптимальному управлению распределением валовых капитальных вложений для достижения оптимального состояния ОПФ .