2.5. Задачи оптимизации и оптимального управления в экономике

Рассмотрим один их центральных блоков в производственно-технологической схеме экономики (см. рис. 2.7) - производство. Его можно представить производственной функцией , значение которой определяет валовый продукт , а аргументами являются природные ресурсы , производственное потребление , трудовые ресурсы и основные производственные фонды (ОПФ) :

.

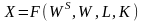Объединяя природные ресурсы и производственное потребление в один аргумент - ресурсы и считая трудовые ресурсы и ОПФ постоянными величинами, можно сформулировать следующую задачу оптимизации:

.

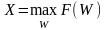В этой задаче максимизируется значение валового продукта путем выбора значения ресурсов как аргумента производственной функции . Причем никаких ограничений на значение не накладывается, поэтому такую задачу называют задачей безусловной оптимизации. Оптимальное значение функции 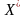достигается при оптимальном решении 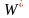, для которого в данной задаче максимизации одновременно выполняются два условия:

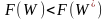
и

.

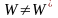Если на выбираемые значения накладываются некоторые ограничения, то рассматриваемая задача приобретает вид:

.

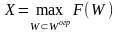Такую задачу называют задачей условной оптимизации и обычно записывают в виде:

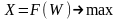
при ограничениях

.

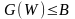В приведенной записи функция 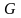и действительное значение представляют ограничения на значения , а функция называется целевой функцией.

Здесь оптимальное значение целевой функции достигается при оптимальном решении , для которого в данной задаче максимизации одновременно выполняются четыре условия:

,

и

,

.

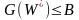Как правило, в реальных задачах ограничения меняются во времени. Т.е. в рассматриваемой задаче действительное значение , определяющее запасы ресурсов , будет зависеть от времени. В этом случае и значение производственной функции также будет зависеть от времени.

Обозначим:

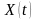- состояние производства,

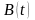- управление производством.

Тогда необходимо выбрать такое управление производством, при котором его состояние будет соответствовать требуемому.

Так формулируется задача оптимального управления, в которой нужно определить оптимальную траекторию управле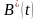ния , приводящую к оптимальной траектории состояния 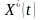. Это требование выражается целевым функционалом (когда аргументы функции сами являются функциями):

,

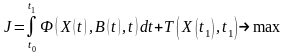где 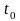- начальный, а 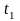- конечный момент времени периода управления 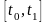, а 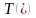- терминальный член. Необходимо также уравнение движения, связывающее между собой функции состояния и управления :

.

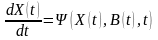Таким образом, в приведенной задаче оптимального управления требуется выбрать в качестве решения такую функцию , определяющую запасы ресурсов в любой момент времени периода управления, которая бы позволила максимизировать функцию валового продукта также в любой момент времени периода управления.

Приведенная выше задача оптимизации является статической, т.е. ее решение отражает состояние в определенный момент времени, а задача оптимального управления - динамической, т.е. ее решение соответствует процессу в определенный период времени. Вот почему и вид решений у них разный: решение задачи оптимизации - численные значения, решение задачи оптимального управления - функции от времени.

Рассмотренная выше (1.3) межотраслевая (межпродуктовая) балансовая модель является статической, т.е. такой, в которой все зависимости отнесены к одному моменту времени. Эта модель может разрабатываться лишь для отдельно взятых периодов, причем в ее рамках на устанавливается связь с предыдущими и последующими периодами. Следовательно, в статических межотраслевых (межпродуктовых) моделях не могут анализироваться распределение, накопление и эффективное потребление капитальных вложений. Капиталовложения вынесены из сферы производства в сферу конечного использования вместе с предметами потребления и непроизводственными затратами, т.е. включены в конечный продукт.

В отличие от статических динамические модели призваны отразить не состояние, а процесс развития экономики, установить непосредственную взаимосвязь между предыдущими и последующими этапами развития и тем самым приблизить анализ к реальным условиям развития экономической системы.

Рассмотрим динамическую модель, являющуюся развитием статической межотраслевой (межпродуктовой) модели, в которой производственные капитальные вложения выделяются из состава конечной продукции, исследуются их структура и влияние на рост объема производства [17].

Вернемся к балансовому соотношению распределения продукции (1.3) модели межотраслевого баланса - межпродуктовому балансу:

,

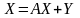или

, .

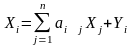В этом статистическом балансе потоки капиталовложений не дифференцируются по отраслям-потребителям и отражаются общей величиной в составе конечной продукции 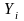каждой -ой отрасли. В динамической схеме распределим конечный продукт на валовые капитальные вложения 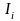и непроизводственное потребление 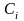(2.4):

.

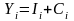Валовые капитальные вложения -ой отрасли представим межотраслевыми потоками капитальных вложений:

,

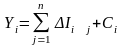где 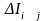- количество продукции -ой отрасли, направленное в текущем периоде в -ую отрасль в качестве производственных капитальных вложений в ее основные фонды. Материально это выражается в приросте в потребляющих отраслях производственного оборудования, сооружений, производственных площадей, транспортных средств и др.

В отличие от потоков текущих затрат (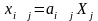 ) межотраслевые потоки капитальных вложений связаны не со всей величиной выпуска продукции в -ой отрасли, а обусловливают прирост продукции .

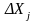Причем допущений о том, что в рассматриваемой модели прирост продукции текущего периода обусловлен вложениями, произведенными в этом же периоде. Если текущий период обозначить через 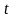, то прирост продукции равен разности абсолютных уровней производства в период и в предыдущий (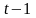 )-ый период:

.

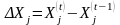Полагая, что прирост продукции пропорционален приросту производственных фондов, можно записать:

; .

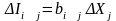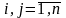Здесь пропорциональность выражают коэффициенты:

; .

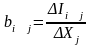Экономический смысл этих коэффициентов заключается в том, что они показывают, какое количество продукции -ой отрасли должно быть вложено в -ую отрасль для увеличения производственной мощности этой отрасли на единицу продукции. Предполагается, что производственные мощности используются полностью и прирост продукции равен приросту мощности. Коэффициенты 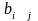называются коэффициентами вложений (приростной фондоемкости).

Используя полученные зависимости, преобразуем систему уравнений распределения продукции модели межотраслевого баланса – межпродуктовый баланс:

, ;

, ;

, .

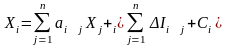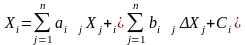Полученная система представляет собой систему линейных разностных уравнений первого порядка. Ее можно привести к обычной системе линейных уравнений, если учесть, что все объемы валовой и конечной продукций относятся к некоторому периоду , а прирост валовой продукции определен в сравнении с ( )-ым периодом:

, .

Отсюда, можно записать следующие соотношения:

, .

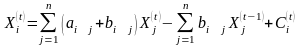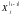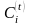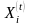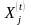Пусть нам известны уровни валовой продукции , , всех отраслей в предыдущем ( )-ом периоде и непроизводственное потребление , , в -ом периоде. Тогда очевидно, что полученные соотношения представляют собой систему линейных уравнений с неизвестными уровнями производства ( ) в -ом периоде. Таким образом, решение такой системы линейных уравнений позволяет определить выпуск продукции в последующем периоде в зависимости от уровня, достигнутого в предыдущем периоде. Связь между периодами устанавливается через коэффициенты вложений , характеризующие фондоемкость единицы прироста продукции.

Переходя от дискретного анализа к непрерывному, будем иметь в пределе:

, .

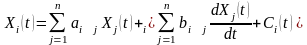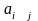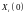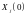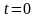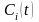Полученные соотношения представляют собой систему линейных дифференциальных уравнений первого порядка с постоянными коэффициентами. Для ее решения помимо коэффициентов прямых затрат и коэффициентов вложений (капитальных затрат) необходимо знать уровни валового выпуска ( ) в начальный момент времени и закон изменения величины непроизводственного потребления, т.е. вида функции . На основе этих данных путем решения получившейся задачи Коши для приведенной системы дифференциальных уравнений можно найти уровни валового выпуска 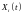теоретически для любого момента времени.