13. Два способа расчета медианы. Модель, заложенная в каждом способе

Способ расчета медианы и, как следствие, получаемое значение искомой величины

определяется модельными соображениями, интерпретацией исходных данных (связанной в первую очередь с нашими представлениями о порождении данных и о соотнесении выборки и генеральной совокупности). Рассмотрим возможные варианты.

а) Выборка – это и есть генеральная совокупность. Кроме названных чисел у нас в принципе ничего нет. Тогда медиану целесообразно найти с помощью вариационного ряда: 112, 113, 115, 119, 119, 120, 120, 120, 122, 126 Ме = 119,5 В таком случае естественной будет следующая функция распределения

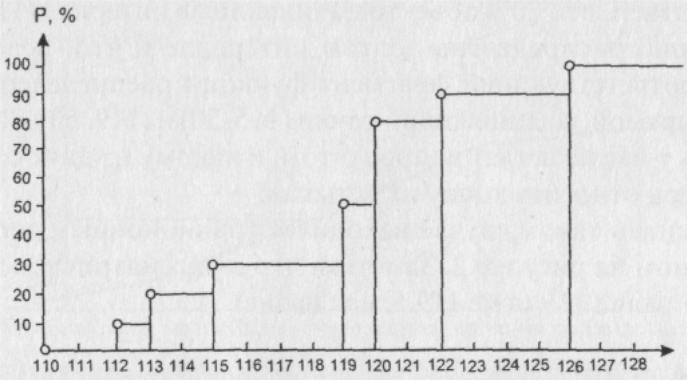
Можно рассчитывать медиану и с помощью построения кумуляты. Это также опирается на предположение о непрерывности рассматриваемого признака. Более того, здесь работает еще одно модельное предположение: объекты внутри каждого интервала распределены равномерно. Подчеркнем, что этот пример хорошо иллюстрирует то, что за каждым математическим методом, даже самым простым, стоит своя модель изучаемого явления. В данном случае - модель понимания средней тенденции. Разбив диапазон изменения признака на интервалы и простроив полигон плотности распределения, мы потеряли информацию о том, как в действительности расположены объекты То, как находятся квантили с помощью кумуляты.

12. Обоснование необходимости расчета мер разброса значений случайной величины (признака). Дисперсия и среднее квадратическое отклонение для дискретной случайной величины (дискретного признака)

Дисперсия- есть математическое ожидание квадрата отклонения, значений случайной величины от ее математического ожидания.

Из математической статистики известно, что самой известной мерой разброса количественного признака является его дисперсия:

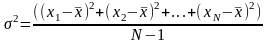
(напомним, что в знаменателе величина объема выборки уменьшается на единицу для того, чтобы сделать соответствующую точечную выборочную оценку дисперсии несмещенной;  – среднее квадратическое отклонение). Ясно, что эта статистика может быть формально адекватной только для интервальных шкал (хотя бы потому, что только при этом условии разумно использование среднего арифметического).

Для порядковых шкал обычно используют какие-либо разницы между квантилями. Например, употребительной мерой является квартильный размах: Q₃ - Q₁. Но, строго говоря, это некорректно, поскольку для порядковой шкалы разности между шкальными значениями не являются осмысленными.

Для более полного описания результатов эмпирического исследования используются меры разброса данных, характеризующие степень индивидуальных отклонений от центральной тенденции. Это самый простой показатель, который можно получить для выборки - разность между максимальной и минимальной величинами данного конкретного вариационного ряда. Мера разброса данных позволяет сравнивать между собой разные группы. Чем сильней варьирует измеряемый признак, тем больше величина разброса данных и наоборот.

Необходимо отметить, что данная мера крайне неточна и неустойчива. Единственный необычно высокий или низкий результат может повлиять на величину размаха.

Более точный метод измерения разброса данных основан на учете разности между каждым индивидуальным результатом и среднеарифметическим значением по группе. Такой мерой разброса является дисперсия или средний квадрат отклонения ( .

Дисперсия характеризует насколько частные значения отклоняются от средней величины в данной выборке. Чем больше дисперсия, тем больше отклонение или разброс данных. Дисперсия определяется по следующей формуле:

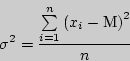где   - дисперсия,  - выражение, означающее, что для всех значений x от первого до последнего в данной выборке вычисляется разность между частными и средними значениями, эти разности возводятся в квадрат и суммируются

n - объем выборки

Вычислим дисперсию (  для следующего ряда: 2, 4, 6, 8, 10. Прежде всего, найдем среднее (М) для данного ряда, оно равно 6.

Из каждого элемента ряда вычтем величину среднего этого ряда. Полученные величины характеризуют то, насколько каждый элемент отклоняется от средней величины в данном ряду. 

Далее разности возводят в квадрат суммируются. Полученную сумму квадратов разностей делим на объем данной выборки. В нашем примере получится следующее:

Общий алгоритм вычисления дисперсии (  следующий:

Вычисляется среднее по выборке

Для каждого элемента выборки вычисляется его отклонение от среднего.

Каждый элемент множества возводят в квадрат.

Находится сумма этих квадратов.

Эта сумма делится на общее количество членов используемой выборки.

Очень часто вместо дисперсии для выявления разброса частных данных относительно средней используют производную от дисперсии величину, называемую стандартным отклонением. Стандартное отклонение равно квадратному корню, извлекаемому из дисперсии ( , и обозначается тем же знаком, только без квадрата ( . Эта величина в ряде случаев оказывается более удобной характеристикой варьирования, чем, дисперсия, так как выражается в тех же единицах, что и средняя арифметическая величина.

В нашем примере 

О чем же свидетельствует стандартное отклонение равное 2, 58? Оно позволяет сказать, что большая часть результатов данного исследования располагается в пределах 2, 58 от средней, т. е. между 3, 42 (6 - 2,58) и 8, 58 (6 + 2,58).