3. Частное (статистическое) определение вер-ти. Относительная частота события как выборочная оценка генеральной совокупности.

Статистическая вероятность события А (будем обозначать Р*(А)) – относит частота (частность) этого события, вычисленная по результатам большого числа испытаний. Это доля благоприятных случаев в общей совокупности.

P*(A) = =

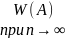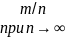
Статистич вер-ть приближенно равна классич вер-ти: Р(А) ≈ P*(A)

Для определения вер-ти выпадения «1» и «2» при подбрасывании кости нам необходимо только знать «модель игры», в данном случае – кость с 6 гранями. Мы можем определить наши шансы теоретически, без подбрасывания кости, - это априорная (до опыта) вер-ть. Во втором примере мы можем определить вер-ть только по результатам опыта, - это апостериорная (после опыта) вер-ть; т.е. классич вер-ть – априорная, а статистич – апостериорная.

Почему мы считаем вер-ть потребительских предпочтений объективной вер-тью? Подобно вер-ти «игры в шансы» она объективна в том смысле, что в нее не включаются индивидуальные суждения.

4. Теорема сложения вероятностей

Вероятность суммы 2х событий равна сумме вероятностей этих событий без вероятности их совместного наступления.

Р(А ᴜ В) = Р(А)+Р(В)-Р(А ʌ В) или Р(А+В) = Р(А)+Р(В)-Р(АВ)

Правило сложения позволяет записать вер-ть объединения этих 2х событий в терминах вер-тей этих 2х событий и вер-ти их пересечения.

Вер-ть пересечения 2х событий Р(А ʌ В) – вер-ть их совместного наступления при проведении эксперимента.

Когда мы складываем вер-ть событий А,В, мы измеряем (взвешиваем) вер-ть их пересечения дважды – 1й раз, когда измеряем относительный размер события А внутри пространства событий, и 2й раз, когда делаем то же самое с событием В. Отсюда, поскольку относит размер, или вер-ть пересечения 2х наборов взвешивается дважды, мы вычитаем одно из них, и, след-но, получаем истинную вер-ть объединения этих 2х событий.

Это правило полезно, когда нам известны отдельные вер-ти событий. Предположим, что вер-ть получения определенной работы равна 0,4; вер-ть получения другой работы 0,5; вер-ть получения двух видов работ равна 0,3. Вер-ть получения хотя бы одной работы равна 0,6 (0,4+0,5-0,3=0,6).

Для несовместных событий их пересечение есть невозможное событие (пустое мн-во), а вер-ть его равна нулю. Два события называются несовместными, если они не пересекаются. Вероятность суммы двух несовместных событий равна сумме вероятностей этих событий.

Для несовместных событий А,В: Р(А ᴜ В) = Р(А)+Р(В) или Р(А+В) = Р(А)+Р(В). Используя основную формулу, если 2 события взаимно несовместны, то вычитают нуль как вер-ть пересечения этих событий.

Правило сложения вероятностей справедливо и для конечного числа n попарно несовместных событий, т.е.: P(A1+A2+A3+...+An) = P(A1) + P(A2) + P(A3) +...+P(An)

Для случая 3х совместных событий можно записать: Р(А+В+С)=Р(А)+Р(В)+Р(С)-Р(АВ)-Р(АС)-Р(ВС)+Р(АВС)

Сумма вер-тей событий 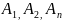, образующих полную группу, равна 1:

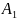Р(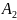 )+Р( )+Р(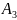 )+…+Р( 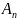)=1 или P

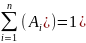
5. Зависимые и независимые события. Теорема умножения вероятностей

События А, В - независимые, если вер-ть каждого из них не зависит от того, произошло или нет другое событие. Вер-ти независимых событий называют безусловными.

События А, В - зависимые, если вер-ть каждого из них зависит от того, произошло или нет другое событие. Вер-ть события В, вычисленная в предположении, что другое событие А уже осуществилось, называется условной вер-тью.

Если 2 события независимы, то справедливы равенства:

Р(В)=Р(В/А); Р(А)=Р(А/В) или Р(В/А)-Р(В)=0

**

Теорема умножения вер-тей: Вер-ть произведения 2х независимых событий А,В равна произведению вер-ти одного из них на условную вер-ть другого:

Ють наступления события В, вычисленная при условии, что событие А уже произошло, равна вер-ти пересечения событий А и В, деленной на вер-ть события А.

Если события А и В независимы, то: вер-ть произведения двух независимых событий А,В равна произведению их вер-тей: Р(АВ)=Р(А)•Р(В)

События А1,А2,…,Аn (n >2) независимые в совокупности, если вер-ть каждого из них не зависит от того, произошли или нет любые события из числа остальных.

Вер-ть совместного появления нескольких событий, независимых в совокупности, равна произведению вер-тей этих событий: Р(А1•А2•А3•Аn) = Р(А1)•Р(А2)•Р(А3)•Р(Аn)

Вер-ть совместного наступления конечного числа зависимых событий равна произведению вер-ти одного из них на условные вер-ти всех остальных, причем условная вер-ть каждого последующего события вычисляется в предположении, что все предыдущие уже наступили:

Р(А1•А2•А3•Аn) = Р(А1)•Р(А2/А1)•Р(А3/А1•А2)•…•Р(Аn/А1•А2•А3•…•Аn)

Вер-ть появления хотя бы одного события из n независимых в совокупности равна разности между 1и произведением вер-тей событий, противоположных данным:

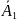Р(А)=1 – Р( ) • Р(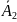 )•…•Р( )

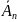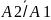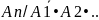Если события А1,А2,…,Аn зависимые в совокупности, то вер-ть наступления хотя бы 1 из них равна: Р(А)=1 – Р( )•Р( )•…• Р . •Аn-1)

Вычисление вер-тей такого типа характеризует эффективность рекламы. Эта вер-ть может означать долю (%) населения, охватываемого рекламой с разной частотой, и отсюда следует оценка рекламных усилий.

6. Формула полной вероятности

Если заранее неизвестно, какое из событий наступит – то это гипотеза.

Если событие А может наступить только вместе с одним из событий , образующих полную группу несовместных событий и называемых гипотезами, то вер-ть события А равна сумме произведений вер-тей каждого из событий на соответствующую условную вероятность события А:

Случай 2х событий:

Р(А)=Р(Н)•Р(А/Н)+Р(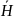 )•Р(А/ )

Случай более 2х событий:

i = 1,2,n

7. Формула Бейеса

Случай 2х событий:

Р(Н/А)=

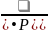
Случай более 2х событий:

Р( =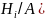

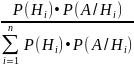
Эти формулы позволяют переоценить вероятности гипотез после того, как становится известным результат испытания, в итоге которого появилось событие А.

Из 1й формулы видно, что вер-ть события Н, задаваемая при условии появления события А, получается из вер-тей событий Н 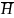и и из условной вер-ти события А при заданном Н. Вер-ти событий Н и - априорные (доопытные, предшествующие), а вер-ть Р(Н/А) – апостериорной (послеопытной, последующей).

8 Дискретные случайные величины. Признак как выборочное представление случайной величины. Полигон распределения и гистограмма (функции плотности распределения). Выборочное представление функции плотности для непрерывного признака. Проблема разбиения диапазона значений признака на интервалы

Дискретной (прерывной) случайной величиной называют случайную величину которая принимает конечное или бесконечное (но счетное) число отдельных, изолированных возможных значений с определенными вероятностями.

Число студентов на лекции – пример подобной величины.

Для дискр. Случ. Величин мы можем перечислить все возможные значения, которые эта величина может принять и их можно представить в виде отдельных точек на числовой оси. Эта совокупность значений может быть задана таблицей, функцией или графиком.

Соотношение, устанавливающее связь между отдельными возможными значениями случ. Величины и соответствующими им вероятностями называется законом распределения дискретной случайной величины. Простейшей формой закона является ряд распределения.

Рядом распределения диск. Случ. Величины Х называется таблица, в которой перечислены возможные (различные) значения этой случайной величины с соответствующими им Вероятностями.

В выборочном социологическом исследовании случайная величина предстает перед социологом в виде признака, для каждого значения которого (а таких значений – конечное количество) известна относительная частота его встречаемости. Эта частота интерпретируется как выборочная оценка соответствующей вероятности. Совокупность частот встречаемости всех значений признака, соответственно, трактуется как выборочное представление функции плотности того распределения вероятностей, которое и задает изучаемую случайную величину.

Пусть, например, вопрос в используемой социологом анкете звучит: “Какова Ваша профессия ?” и сопровождается 5-ю вариантами ответов, закодированных числами от 1 до 5. Тогда частотное распределение - аналог функции плотности - будет иметь, например, вид:

Таблица 1.