1. События, алгебра событий, основные их виды. Главные события для социолога, состоящие в том, что какие-то признаки принимают какие-либо значения.

Математическим описанием связей между событиями занимается алгебра событий. Алгебру событий называют алгеброй Буля по имени английского математика Дж. Буля (1815–1864).

Для того чтобы понять смысл вероятности, напомним некоторые понятия теории множеств и операции над множествами.

Множество – это совокупность, набор, коллекция, собрание каких-либо элементов, объединенных по определенному признаку. Число элементов в множестве может быть конечным и бесконечным (например, все числа, лежащие между 0 и 1).

Полное множество Х – набор, содержащий все элементы в заданном контексте.

Пустое множество Ø – набор, не содержащий элементов. Всякое подмножество X есть множество (например, множество А, Ā и Ø). Задав набор А, можно определить его дополнение. Дополнением Ā множества А является набор, содержащий все элементы из полного набора X, которые не являются элементами набора А.

Диаграммы Венна, названные по имени английского логика Дж. Венна, наглядно представляют операции множеств и связанные с ними соотношения. На диаграммах Венна множество обозначается кругом, эллипсом или другой геометрической фигурой внутри прямоугольника, обозначающего полное множество.

Взаимоотношение между набором А и его дополнением показано на рис. 1.1, а.

Пример 1.1. Пусть полный набор – все студенты института. Определим А – множество студентов, сдавших летнюю сессию только на «отлично». Дополнение А есть – множество студентов неотличников. В сумме А и – все студенты института.

Рассмотрим подмножества А и В внутри полного множества X. Определим пересечение А и В.

Пересечение А и В (обозначается как А∩В) есть набор, содержащий все элементы, которые являются членами и А и В (см. рис. 1.1, б).

Объединение А и В (обозначается А В) есть набор, содержащий все элементы, которые являются членами или А, или В, или А и В вместе (см. рис. 1.1, в).

Продолжим рассмотрение примера со студентами. Определим В как множество студентов, сдавших зимнюю сессию на «отлично». Тогда пересечение А и В – подмножество студентов, сдавших на «отлично» и летнюю, и зимнюю сессии.

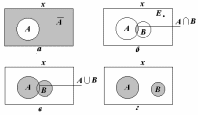
Объединение А и В – подмножество студентов, которые сдали на «отлично» или летнюю, или зимнюю, или обе сессии.

Два набора могут не иметь пересечения. В этом случае мы говорим, что пересечение А и В есть пустое множество (см. рис. 1.1, г). В примере с успеваемостью студентов подмножество студентов, получивших двойки в летнюю сессию, не пересекается с подмножеством отличников.

                       

1.2. Основные определения: испытание, событие.

Классификация событий

Опыт (эксперимент, испытание) – это ситуация с более чем од­ним возможным исходом, из которых всегда имеет место точно одно так называемое элементарное событие. Исходом опыта может быть результат наблюдения или измерения.

Извлечение карты из колоды – эксперимент. Один из исходов эксперимента – извлечение дамы бубен. Бубновую даму можно извлечь из колоды, содержащей 36 карт и 52 карты. Число карт – условие испытания.

Единичный, отдельный исход эксперимента называется элементарным событием. Набор всех элементарных событий – пространство событий (множество).

Извлечение любой карты из колоды – элементарное событие. Полному набору событий соответствует полное множество X, относящееся к заданному эксперименту. Полный набор событий – набор всех возможных исходов эксперимента. Элементарному событию соответствует только одна точка пространства событий. Аналогом элементарного события является элемент множества.

Теория вероятностей изучает случайные события. Случайным событием называется событие, которое может произойти или не произойти в результате некоторого эксперимента (далее будем опускать термин «случайный»).

Событие – это любое подмножество пространства событий, набор элементарных исходов. В диаграммах Венна событию соответствует подмножество элементарных событий. Событие произошло, если в результате эксперимента произошло элементарное событие, принадлежащее этому поднабору. Например, элементарные события – «туз конкретной масти» – благоприятствуют случайному событию «туз».

События обычно обозначаются заглавными буквами латинского алфавита: А, В, С, D, Е, F и т. д. События можно классифицировать.

Достоверное событие – это событие, которое обязательно произойдет в результате испытания (подброшенный камень обязательно упадет на Землю вследствие действия закона притяжения). Достоверные события условимся обозначать символом Ω.

Невозможное событие – это событие, которое не может произойти в результате данного опыта (извлечение черного шара из урны с белыми шарами есть событие невозможное). Невозможное событие обозначим Ø.