Уравнение бегущей волны

        Уравнение плоской одномерной синусоидальной волны:

        (Вместо синуса можно написать косинус.) Это уравнение отличается от уравнения синусоидальных колебаний тем, что колеблющая величина S зависит не только от времени, но и от координаты. Это и понятно: вместо одного маятника мы имеем множество связанных маятников - частиц среды. v - скорость распространения волны, А - амплитуда волны, аргумент синуса - фаза волны, _ - начальная фаза колебаний в точке х = 0,  - частота (циклическая) волны.

        Расстояние, на которое распространяется волна за время, равное периоду колебаний, называется ДЛИНОЙ ВОЛНЫ  = .

        ВОЛНОВОЕ ЧИСЛО k:

        С помощью введенного волнового числа уравнение волны запишется:

        Если мы рассматриваем не одномерную волну, удобно наряду с волновым числом ввести ВОЛНОВОЙ ВЕКТОР k, модуль которого равен волновому числу, а направление совпадает с направлением луча (направлением распространения волны). В векторном виде уравнение волны будет выглядеть так:

здесь r - радиус вектор точки пространства; _- начальная фаза колебаний в начале координат.

     Уравнение сферической волны отличается тем, что амплитуда волны убывает с расстоянием от источника:

_= const по смыслу формулы есть амплитуда волны на единичном расстоянии от источника.

        Уравнение волны в дифференциальной форме обычно называют волновым уравнением; вид этого уравнения следующий:

     или    

Здесь S - оператор

Лапласа:

        Уравнение синусоидальной волны является решением волнового уравнения (можно проверить подстановкой). Общее же решение волнового уравнения следующее:

        Здесь А и В - произвольные константы, а f₁ и f₂ - произвольные дважды дифференцируемые функции. Первое слагаемое описывает волну, распространяющуюся слева направо, второе - встречную волну.

Нетрудно написать уравнение сферической волны. Положение колеблющейся частицы определяется в этом случае только ее расстоянием от источника колебаний r, т.е. фаза колебаний должна иметь вид ωt – kr + . Амплитуда колебаний в сферической волне, однако, не будет оставаться постоянной — она убывает с расстоянием, как 1/r. Последнее утверждение вытекает из требования, чтобы поток энергии, переносимый волной через поверхность сферы любого, сколь угодно большого, радиуса оставался постоянным. Таким образом, сферическая волна должна иметь следующий вид:

u(r,t) = cos(ωt – kr + ),                                                       (3.54)

где a— постоянная величина, численно равная амплитуде волны на расстоянии от источника, равном единице длины.

 

 

 

 

 

 

 

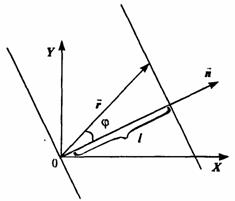
Найдем уравнение плоской волны, бегущей в трехмерном пространстве вдоль произвольного направления n. Выберем систему координат и возьмем волновую поверхность волны, находящуюся на расстоянии  от начала координат (рис.). Это будет плоскость, перпендикулярная вектору n. Если волна в начале координат задана уравнением:

u(0,t) = u₀cos(ωt + ),                                                             

то колебания частиц на выбранной волновой поверхности будут иметь вид:

u(0,t) = u₀cos(ωt –k + ).                                                       

Из рис. видно, что  = rcos =  , поэтому написанному выше уравнению можно придать вид:

u( ,t) = u₀cos(ωt - k  + ).                                                        

Введем вектор

,                                                                   (3.55)

равный по величине волновому числу и направленный вдоль вектора n направления распространения волны. Величина  называется волновым вектором. С его помощью уравнение плоской бегущей волны, распространяющейся в произвольном направлении n, приобретает вид:

u( ,t)= u₀cos(ωt –  + ).                                      (3.56)

Получим с помощью выражения (3.56) общий вид волнового уравнения, частным видом которого является (3.50). Колебания частиц в волне являются функцией четырех переменных — трех пространственных координат x, y, z и времени t. Продифференцируем выражение (3.56) по каждой из этих переменных дважды, пользуясь тем, что  = k_x+ k_y+ k_z:

                                    

Складывая производные по координатам и выражая правую часть полученного выражения через производную по времени, находим:

.                                          

Наконец, заменяя ω/k на фазовую скорость волны (3.52), окончательно получаем:

.                                               (3.57)

Это и есть общий вид волнового уравнения, который был выведен исходя из того, что выражение (3.51) представляет собой плоскую волну. На самом деле класс решений уравнения (3.57) необычайно широк. Всякая функция, котораяудовлетворяет уравнению(5.57), описывает какую-либо волну. Например, решением этого уравнения является и сферическая волна (3.54). Волны могут быть и более сложной формы.

Частным случаем уравнения (3.57) является одномерная волна (3.50) – в этом случае колебания в волне не зависят от остальных координат.

Интерференция волн — взаимное увеличение или уменьшение результирующей амплитуды двух или нескольких когерентных волн, одновременно распространяющихся в пространстве.^[1] Сопровождается чередованием максимумов и минимумов (пучностей) интенсивности в пространстве. Результат интерференции (интерференционная картина) зависит от разности фаз накладывающихся волн.

Дифракция Волн - явление огибания волнами препятствий и проникновение их в область геометрической тени. Явление дифракции можно качественно объяснить применением принципа Гюйгенса к распространению волн в среде при наличии преград.

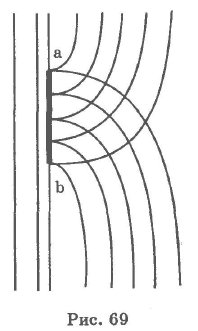
Рассмотрим плоскую преграду ab (рис. 69). На рисунке показаны построенные по принципу Гюйгенса волновые поверхности позади преграды. Видно, что волны действи-

тельно загибаются в область тени. Но принцип Гюйгенса ничего не говорит об амплитуде колебаний в волне за преградой. Ее можно найти, рассматривая интерференцию волн, приходящих в область геометрической тени. Распределение амплитуд колебаний позади преграды называется дифракционной картиной. Полный вид дифракционной картины позади преграды зависит от соотношения между длиной волны Л, размером преграды d и расстоянием L от преграды до точки наблюдения. Если длина волны Л больше размеров преграды d, то волна его почти не замечает. Если длина волны Л одного порядка с размером преграды d, то дифракция проявляется даже на очень малом расстоянии L, и волны за преградой лишь чуть-чуть слабее, чем в свободном волновом поле с обеих сторон. Если, наконец, длины волн много меньше размеров препятствия, то дифракционную картину можно наблюдать только на большом расстоянии от преграды, величина которой зависит от Л и d.

Стоя́чая волна́ — колебания в распределённых колебательных системах с характерным расположением чередующихся максимумов (пучностей) и минимумов (узлов) амплитуды. Практически такая волна возникает при отражениях от преград и неоднородностей в результате наложения отражённой волны на падающую. При этом крайне важное значение имеет частота, фаза и коэффициент затухания волны в месте отражения.