2.5. Закон полного тока

Циркуляцией вектора  магнитной индукции вдоль замкнутого контура  называется интеграл вида:

 

,                             (2.11)

где  – замкнутый контур произвольной формы;  – вектор элементарной длины контура, направленный вдоль обхода контура.

Закон полного тока для магнитного поля в вакууме: циркуляция вектора индукции магнитного поля вдоль замкнутого контура в вакууме пропорциональна алгебраической сумме токов, охватываемых этим контуром:

 

,                                 (2.12)

 

где  – магнитная постоянная;  – число проводников с токами, охватываемых контуром  произвольной формы.

Закон справедлив для проводников с токами любой формы и любых размеров.

В отличие от электростатического потенциального поля, в котором циркуляция вектора напряженности электрического поля  вдоль любого замкнутого контура равна нулю, магнитное поле является вихревым (вихревое магнитное поле). В таком поле циркуляция вектора  индукции магнитного поля вдоль замкнутого контура отлична от нуля. Если контур  не охватывает токи, то циркуляция вектора  вдоль этого контура равна нулю. Однако это не изменяет вихревого характера магнитного поля.

Закон полного тока применяют для расчета магнитных полей, и он имеет такое же значение, как и теорема Остроградского – Гаусса для расчета электрических полей в электростатике.

П рименим этот закон для расчета магнитного поля соленоида (рис. 2.5).

Под соленоидом понимается совокупность одинаково последовательно соединенных витков, равномерно навитых на общий каркас.

Применим теорему циркуляции индукции магнитного поля к произвольному контуру 1-2-3-4-1, взятому в виде прямоугольника:

,

где N – число витков (токов), охватываемых контуром.

На участках 1-2 и 3-4 проекция вектора индукции на направление обхода равна нулю. Следовательно,

 

.

 

Для случая бесконечно длинного соленоида, который рассматривается здесь, магнитное поле целиком сосредоточено внутри него, и практически индукция поля вне соленоида равна нулю.

Следовательно,

.

Таким образом,

,

где  – длина стороны 2-3 контура.

 

,                                        (2.13)

 

где  – число витков на единицу длины соленоида, тогда

 

,                                        (2.14)

 

Для среды с магнитной проницаемостью  формула (2.14) принимает вид:

.                                        (2.15)

 

Из выражения (2.15) следует, что во всех точках бесконечно длинного соленоида индукция магнитного поля одинакова по величине и направлению, т.е. магнитное поле соленоида является однородным. Однако в реальных соленоидах, имеющих конечную длину, при приближении к краям соленоида будет наблюдаться краевой эффект (рис. 2.5), который можно устранить, если придать соленоиду форму тороида.

В общем случае соленоид, создающий однородное магнитное поле, в магнетизме аналогичен конденсатору, создающему однородное электрическое поле в электростатике.

3. Определение единицы силы тока - ампера - основано на взаимодействии параллельных прямолинейных токов: ампер ( а) равен силе постоянного тока, который, протекая по двум длинным параллельным прямолинейным проводникам, расположенным на расстоянии 1 м один от другого в вакууме, вызывает между этими проводниками силу, равную 2 10 - 7 н на 1 м длины. 

Сила взаимодействия двух прямолинейных проводников бесконечной длины
Проводники с токами одинаковых направлений притягиваются, а с токами противоположных направлений - отталкиваются. 4.

Сила Лоренца — сила, с которой, в рамках классической физики, электромагнитное поле действует на точечную заряженную частицу. Иногда силой Лоренца называют силу, действующую на движущийся со скоростью заряд лишь со стороны магнитного поля, нередко же полную силу — со стороны электромагнитного поля вообще^[1], иначе говоря, со стороны электрического и магнитного полей. Выражается в СИ как:

Заряженная частица

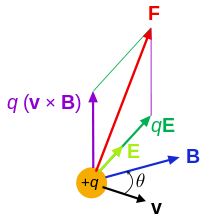
Сила Лоренца f действующая на заряженную частицу (заряда q) при движении (с постоянной скоростью v). E поле и B поле меняются в пространстве и во времени.

Сила F действующая на частицу с электрическим зарядом q, движущуюся с постоянной скоростью v, во внешнем электрическом E и магнитном B полях, такова:

где × векторное произведение. Все величины выделенные жирным являются векторами. Более явно:

где r — радиус-вектор заряженной частицы, t — время, точкой обозначена производная по времени.

Непрерывное распределение заряда

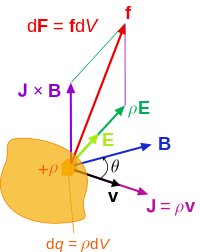
Сила Лоренца (на единичный 3-объём) f действующая на непрерывное распределение заряда (зарядовая плотность ρ) при движении. 3-плотность потока J соответствует движению заряженного элемента dq в объеме dV .

Для непрерывного распределения заряда, сила Лоренца принимает вид:

где dF — сила, действующая на маленький элемент dq.

5. Электромагнитная индукция — явление возникновения электрического тока в замкнутом контуре при изменении магнитного потока, проходящего через него.

Закон Фарадея

Согласно закону электромагнитной индукции Фарадея (в СИ):

где

 — электродвижущая сила, действующая вдоль произвольно выбранного контура,

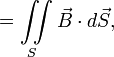 — магнитный поток через поверхность, натянутую на этот контур.

Знак «минус» в формуле отражает правило Ленца, названное так по имени русского физика Э. Х. Ленца:

Индукционный ток, возникающий в замкнутом проводящем контуре, имеет такое направление, что создаваемое им магнитное поле противодействует тому изменению магнитного потока, которым был вызван данный ток.

Для катушки, находящейся в переменном магнитном поле, закон Фарадея можно записать следующим образом:

где

 — электродвижущая сила,

 — число витков,

 — магнитный поток через один виток,

 — потокосцепление катушки.

Векторная форма

В дифференциальной форме закон Фарадея можно записать в следующем виде:

(в системе СИ)

или

(в системе СГС).

В интегральной форме (эквивалентной):

(СИ)

или

(СГС)

Здесь  — напряжённость электрического поля,  — магнитная индукция,  — произвольная поверхность,  — её граница. Контур интегрирования подразумевается фиксированным (неподвижным).

Правило Ленца определяет направление индукционного тока и гласит:

Индукционный ток всегда имеет такое направление, что он ослабляет действие причины, возбуждающей этот ток.

Согласно закону электромагнитной индукции Фарадея при изменении магнитного потока , пронизывающего электрический контур, в нём возбуждается ток, называемый индукционным. Величина электродвижущей силы, ответственной за этот ток, определяется уравнением^[1]:

где знак «минус» означает, что ЭДС индукции действует так, что индукционный ток препятствует изменению потока. Этот факт и отражён в правиле Ленца.

Начало формы

толкования переводы книги фильмы

Конец формы

6.