3. Класифікація випадкових процесів.

Випадковий процес, що розглядається в будь-якій фізичній системі, являє собою випадкові переходи системи з одного стану в інший. Залежно від множини цих станів , від множини значень аргументу всі випадкові процеси розподіляють на класи:

– Дискретний процес (дискретний стан) з дискретним часом.

– Дискретний процес з неперервним часом.

– Неперервний процес (неперервний стан) з дискретним часом.

– Неперервний процес з неперервним часом.

У першому та третьому випадках множина станів є дискретною, тобто аргумент приймає лише дискретні значення (зазвичай, ); у першому випадку множи­на значень випадкової величини , тобто – дискретна множина (тобто множина є скінченною або зліченною), у третьому випадку множина є незліченною, тобто переріз випадкового процесу в будь-який момент часу являє собою неперервну випадкову величину.

У другому та четвертому випадках множина неперервна, в другому випадку множина станів є скінченною або зліченною, а в четвертому незліченна множина.

Наведемо приклади відповідних класів процесів.

1. Тенісист може отримати певну кількість очок під час турніру, матчі відбуваються у певний момент (відповідно до розкладу турніру) часу Випадковий процес — кількість забитих голів до моменту часу .

2. — кількість отриманих абонентом телефонних дзвінків протягом дня до моменту .

3. У певні моменти часу фіксується ціна на пальне . Це випадковий процес неперервного типу з дискретним часом.

4. Серцевий тиск людини .

Вивчають випадкові процеси залежно від їх типу різними методами.

3. Основні характеристики випадкових процесів.

Як і у випадку випадкових величин, випадковим процесам ставляться у відповідність певні числові характеристики. Інформації про числові характеристики процесу достатньо для розв’я­зання багатьох практичних задач. Ускладнення, порівняно з випадковими величинами, полягає у тому, що числові характеристики випадкових процесів представляються в загальному випадку не числами, а функціями.

Означення. Математичним сподіванням ВП називають невипадкову функцію , яка в будь-який момент часу дорівнює математичному сподіванню відповідного перерізу випадкового процесу, тобто

(21.1)

Позначають математичне сподівання або .

Як і випадку математичного сподівання випадкової величини, функція характеризує поведінку ВП в середньому. Геометрична інтерпретація математичного сподівання така: це «середня крива», навколо якої розташовані графіки функцій реалізацій випадкового процесу (рис. 21.2).

Рис. 21.2

Основні властивості математичного сподівання та невипадкових функцій дають змогу сформулювати основні властивості математичного сподівання випадкових процесів.

1. Математичне сподівання невипадкової функції дорівнює самій невипадковій функції, тобто

.

2. Невипадковий множник можна винести за знак математичного сподівання випадкового процесу, тобто

3. Математичне сподівання алгебраїчної суми двох випадкових процесів дорівнює алгебраїчній сумі математичних сподівань доданків, тобто

.

Зауваження. Зафіксувавши аргумент при переході від випадкового процесу до випадкової величини (тобто до зрізу випадкового процесу), можна знайти математичне сподівання цього процесу.

Таким чином, якщо ВП при даному є неперервна випадкова величина з щільністю розподілу , то його математичне сподівання можна знайти за формулою:

. (21.2)

Приклад 1. Знайти математичне сподівання випадкового про­цесу , що задається формулою , ( – випадкова величина розподілена за нормальним законом з ).

Розв’язання. 1 спосіб. Щільність розподілу ВВ Х має вигляд , використовуючи формулу (2) обчислюємо: ,

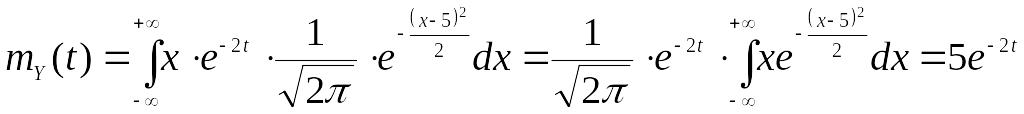так як .

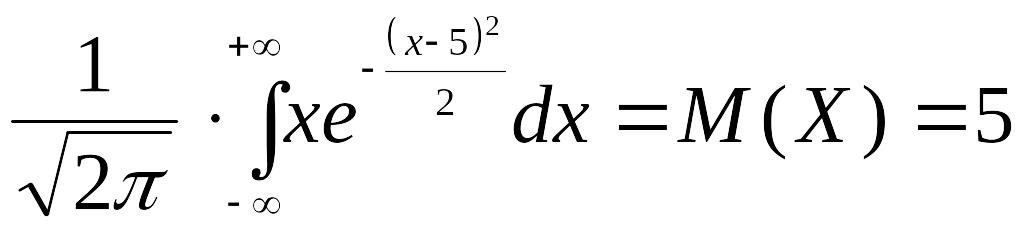Власне результат можна було б отримати і в інший спосіб, використовуючи властивість 2 математичного сподівання випадкового процесу:

.

Але відповідно до умови задачі , тобто і відповідно .

Означення. Дисперсією випадкового процесу називається невипадкова функція , яка при кожному значенні дорівнює дисперсії відповідного зрізу

(21.3)

Дисперсія випадкового процесу характеризує розсіювання можливих значень випадкового процесу навколо його математичного сподівання.

Разом з дисперсією ВП розглядається і така числова характеристика як середнє квадратичне відхилення , що визначається рівністю

. (21.4)

Розмірність функції середнє квадратичне відхилення збігається з розмірністю ВП .

Сформулюємо основні властивості дисперсії випадкового процесу:

1. Дисперсія невипадкової функції дорівнює нулю, тобто

.

2. Дисперсія ВП є невід’ємною функцією:

.

3. Дисперсія добутку невипадкової функції на випадкову функцію дорівнює добутку квадрату невипадкової функції на дисперсію випадкової функції, тобто

.

4. Дисперсія суми ВП та невипадкової функції дорівнює дис­персії ВП, тобто

.

Приклад 21.2. Використовуючи умови прикладу 21.1, знайти дисперсію та середнє квадратичне відхилення.

Розв’язання. Знайдемо дисперсію, використовуючи властивість 3: , за умови , тобто . Тому , відповідно .

Математичне сподівання та дисперсія не є вичерпуючими характеристиками випадкового процесу, знаючи лише ці дві характеристики, наприклад, не можна зробити висновок про залежність двох або більше перерізів ВП. Саме для характеризації зв’язку між різними перерізами ВП використовують кореляційну функцію. Аналогом даної числової характеристики у випадкових величинах є коваріація, або кореляційний момент:

,

що характеризує ступінь зв’язку між двома випадковими величинами та .

Означення. Кореляційною (коваріаційною, автоковаріаційною, авто- кореляційною) функцією ВП називають невипадкову функцію двох аргументів , яка при кожній парі значень та дорівнює кореляційному моменту (коваріації) відповідних перерізів та :

,

або

,

де – центрована випадкова функція.

Сформулюємо основні властивості кореляційної функції випадкового процесу .

1. Кореляційна функція при однакових значеннях аргументів дорівнює дисперсії випадкового процесу, тобто

.

Доведення. Дійсно,

.

Зауваження. Дана властивість дозволяє вважати математичне сподівання та кореляційну функцію головними числовими характеристиками випадкового процесу.

2. Кореляційна функція не змінюється при перестановці аргументів місцями, тобто .

3. Якщо до випадкового процесу додати випадкову функцію, то кореляційна функція не зміниться, тобто, якщо , то

.

Доведення. Відповідно до властивості математичного сподівання , то , звідси безпосередньо випливає, що = .

4. Модуль кореляційної функції не перевищує добуток середніх квадратичних відхилень, тобто

.

Ця властивість випливає з відповідної властивості кореляційного моменту двох ВВ та з урахуванням першої властивості кореляційної функції ВП.

5. При множенні ВП на невипадковий множник її кореляційна функція помножиться на добуток , тобто, якщо , то

.

Поряд з кореляційною функцією ВП розглядається також нормована кореляційна функція ( або нормована автоковаріаційна функція) .

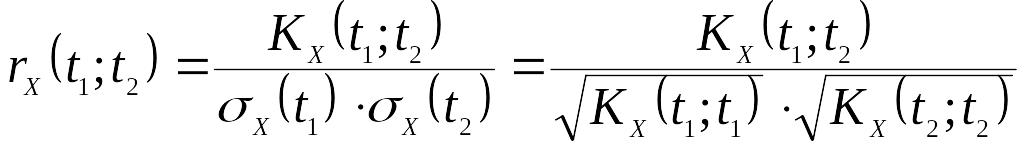За своїм імовірністним змістом є певним аналогом коефіцієнту кореляції для двох ВВ, але не є сталою величиною, а залежить від аргументів та .

Безпосереднім наслідком означення нормованої автокореляційної функції та основних властивостей кореляційної функції ВП є такі властивості :

1. .

2. .

3. .

Приклад 21.3. Використовуючи умови прикладу 21.1, знайти кореляційну та нормовану кореляційну функцію випадкового процесу .

Розв’язання. Використовуючи означення кореляційної функції випадкових процесів, отримуємо:

= .

Тобто . Відповідно .

Для визначення ступені взаємозв’язку зрізів двох випадкових процесів використовують кореляційну функцію зв’язку або взаємну кореляційну функцію.

Означення. Взаємною кореляційною функцією двох випадкових процесів та називається невипадкова функція двох незалежних аргументів та , яка для кожної пари значень та дорівнює кореляційному моменту двох перерізів та :

.

Означення. Два випадкових процеси та називаються некорельованими, якщо їх взаємна кореляційна функція тотожньо дорівнює нулю, тобто, якщо для будь-яких та . У випадку, коли випадкові процеси та називаються корельованими (пов’язаними).

Сформульовані вище властивості кореляційного моменту дають можливість сформулювати ряд властивостей взаємної кореляційної функції.

1. При одночасній перестановці індексів та аргументів взаємна кореляційна функція не змінюється, тобто

.

2. Модуль взаємної кореляційної функції двох випадкових процесів не перевищує добутку їх середніх квадратичних відхилень, тобто

.

3. Кореляційна функція не зміниться, якщо до випадкових процесів та додати невипадкові функції та відповідно, тобто , тут .

4. Невипадкові множники можуть бути винесені за знак кореляційної функції, тобто, якщо , то

.

5. Якщо , то

.

6. Якщо випадкові процеси та некорельовані, то ко­реляційна функція їх суми дорівнює сумі їх кореляційних функцій:

.

Оцінюють ступінь залежності перерізів двох випадкових процесів за допомогою нормованої взаємної кореляційної функції , що визначається рівністю:

.

Функція має такі самі властивості, як і функція за виключенням другої властивості, яка заміняється на наступну: .

Приклад 21.4. Знайти взаємну кореляційну функцію двох випадкових процесів , де – випадкова величина, для якої .

Розв’язання. Обчислимо та :

.

Використовуючи означення взаємної кореляційної функції випадкових процесів, маємо:

.

Остаточно .

4. Випадковий процес, стаціонарний у широкому сенсі.

Важливим класом випадкових процесів є стаціонарні ВП, тобто такі, що не змінюють свої характеристики з часом. Ці процеси мають вигляд неперервних випадкових коливань навколо деякого середнього значення. Такими процесами є тиск людини, коливання напруги в електричній мережі тощо.

Означення. Випадковий процес називається стаціонарним у широкому сенсі, якщо його математичне сподівання є сталою, а кореляційна функція залежить лише від різниці аргументів, тобто

.

З означення стаціонарного в широкому сенсі випадкового процесу випливає, що його кореляційна функція є функцією одного аргументу, тобто

.

Нижче сформульовані основні властивості кореляційної функції стаціонарного випадкового процесу СВП.

1. Дисперсія СВП є величиною сталою і дорівнює значенню кореляційної функції в нулі, тобто

.

2. Кореляційна функція СВП є функцією парною, тобто

.

3. Модуль кореляційної функції СВП не перевищує її значення при , тобто

.

4. Нормована кореляційна функція СВП є невипадковою функцією аргументу :

.

Має місце нерівність .

Більшість СВП мають важливу для практики властивість ергодичності. Суть цієї властивості полягає в тому, що по одній, достатньо тривалій реалізації, можна зробити висновок про всі властивості процесу, так само як по будь-якій кількості реалізацій. Тобто окремі характеристики СВП, а саме можуть бути визначені як відповідно середнє по часу для однієї реалізації але досить тривалої.

Зауваження. Ергодичні ВП є стаціонарними у вузькому сенсі, зворотне твердження взагалі неправильне.

Достатньою умовою ергодичності ВП щодо математичного сподівання та кореляційної функції є прямування до нуля його кореляційної функції при , тобто .

Як оцінки характеристик ергодичних СВП приймають усереднене за часом значення

.

Інтеграли в правих частинах рівностей на практиці розраховують наближено.

Випадкові процеси та називають стаціонарно пов’язаними, якщо їх взаємна кореляційна функція залежить лише від .

Як приклад стаціонарного процесу розглянемо випадковий процес - гармонійне коливання. Розрахунки дають ,

.