2 Постоянные и переменные факторы производства и проблема их оптимального сочетания. Производственная функция.
Для осуществления производственной деятельности предприятию необходимы факторы производства, основными из которых являются труд, земля и капитал.
Применяемые в производстве факторы подразделяются на постоянные (фиксированные) и переменные.
К постоянным относят количественные масштабы, которые невозможно изменить на данном временном отрезке.
К переменным относят производственные факторы, количественный состав которых может быть изменен на данном временном отрезке.
Производство определенного продукта требует использования какого-то сочетания факторов производства, и отсутствие некоторого из них может привести к остановке производства, следовательно факторы производства являются взаимодополняемыми.
Если имеются в наличии все производственные факторы, то при прочих равных условиях объем производимой продукции будет зависеть от количества вводимых факторов. Зависимость между объемом выпуска и количеством применяемых факторов выражается производственной функцией.
Q = f(x1, x2, . . . , xn), где
Q – количество произведенной продукции
x1, x2, xn – используемые факторы производства
Производственная функция показывает максимально возможный выпуск продукции, которую может произвести фирма при каждом конкретном сочетании факторов производства. Она строится для определенной технологии и применение более совершенной технологии увеличивает объем выпуска при любой комбинации факторов производства описывается уже новой производственной функцией.
Объем произведенной продукции зависит не только от количества используемых факторов, но и от комбинации, в которой они применяются, следовательно кроме взаимодополняемости производственные факторы характеризуются и взаимозаменяемостью, то есть они могут использоваться в производственном процессе в различных пропорциях, замещая друг друга.
Существуют определенные границы замещения одних факторов другими. Они обусловлены научно-техническим прогрессом уровнем технологий.
В некоторых производственных процессах вводимые факторы могут применяться только в строго фиксированных пропорциях, их взаимозамена технически невозможна и недопустима.
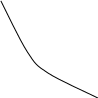
Каждой из имеющихся производственной технике соответствует ряд определенных комбинаций, используемых факторов. Применяемые два фактора: труд и капитал и некоторая конкретно данная технология, позволяет применить четыре комбинации для достижения данного объема производства. Q = 10 ед.
Комби- нации |
Количество единиц |
|
капитала, Qк |
труда, QL |
|
A |
5 |
1 |
B |
3 |
2 |
C |
2 |
3 |
D |
1 |
5 |
Qк (ед.)
5
A
4
3
B
2
C
1
D
0 1 2 3 4 5 QL (ед.)
Для достижения объема выпуска равного 10 единицам можно использовать различные комбинации. Если применить комбинацию А (Qк=5, QL=1 ), то эта комбинация наиболее капиталоемкая, а комбинация D более трудоемкая. Соединив точки A, B, C и D получаем кривую, называемую изоквантой выпуска 10 единиц продукции.
Изокванта (iso – «тот же самый», quant – «количество») – это кривая, точки на которой показывают различные комбинации использованных факторов, при которых производится одинаковый объем продукции.
Изокванта имеет вогнутый вид – сокращение количества потребления фактора капитала при движении вдоль изокванты требует соответствующего увеличения количества факторов труда, чтобы не допустить снижения объема производства.
Q
к
(ед.)
Q = 15 ед.
Q = 10 ед.
Q = 5 ед.
QL
(ед.)
Эти изокванты образуют карту изоквант. Каждая из изоквант, расположенная правее и выше, показывает увеличение объема выпуска.
Изокванты могут проходить через любую точку на графике. Изокванты аналогичны кривым безразличия, которые отражают альтернативные варианты потребительского выбора продуктов, а Изокванты отражают альтернативные комбинации затрат факторов производства для выпуска определенного объема продукции.
Изокванты свидетельствуют о возможностях фирмы гибко принимать производственные решения, однако существуют некоторые ограничения, в частности, продолжительность временного интервала, в рамках которого протекает производственный процесс. Количество переменных факторов можно изменить за сравнительно больший промежуток времени. В зависимости от времени, затрачиваемого на изменение количества применяемых факторов различают кратко- и долгосрочный периоды в деятельности фирмы (зависит от количества изменяемых факторов).
Для упрощения чаще всего используются производственные функции с двумя ресурсами: трудом и капиталом, следовательно производственная функция двух ресурсов имеет вид:
Q = f (QL ;Qк)
Производственные функции могут иметь разные области использования, в основном они применяются для решения задач анализа, планирования и прогнозирования производства. Достаточно часто применяется производственная функция Кобба-Дугласа. В основном она используется для планирования и моделирования производства на макроуровне.
Q = A·Qαk·QβL ,
где А – независимый коэффициент
α и β – показатели эластичности выпуска по затратам ресурсов труда и капитала
Если затраты на капитал увеличатся на 1%, это приводит к увеличению выпуска на α%, а увеличение затрат труда на 1 % приводит к увеличению выпуска на β%.
А, α и β – const
А – коэффициент, учитывающий влияние факторов, не вошедших в уравнение Кобба-Дугласа и их конкретные числовые значения определяются на основе статистических данных с помощью корреляционных методов.
Если функция Кобба-Дугласа имеет вид:
Q = A·Qαk·Q1-αL
т.е. сумма степенных показателей равна 1, то функция Кобба-Дугласа является однородной, т.е. она демонстрирует постоянную отдачу при изменении масштабов производства (увеличение затрат на труд или (и) капитал на 1%) приводит к увеличению выпуска на 1%.
Производственная функция Кобба-Дугласа устанавливает зависимость величины созданного общественного продукта от совокупных затрат живого труда и суммарного объема применяемых производственных факторов.
Существуют также производственные функции Леонтьева и Конторовича.
Как было сказано выше, изокванта отображает возможные сочетания двух ресурсов для производства определенного объема продукции.
Зная доход предприятия и цены ресурсов, можно построить изокосту (с лат. iso – «тот же самый», cost – «цена ресурсов»). Каждая точка на изокосте показывает одну и ту же сумму денег. т.е. сочетание ресурсов, которое производитель может приобрести.
Q
к
(ед.)
tg α = const
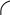
α
QL (ед.)
Если доход предприятия увеличивается, изокоста смещается параллельно вправо вверх, при этом производитель может увеличить объем выпуска продукции при условии, что цены ресурсов прежние.
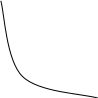
Графически равновесие производителя можно изобразить следующим образом :
Qк (ед.)
Qк
А
Q = 30 ед.
Q = 20 ед.
Q
= 10 ед.
QL QL (ед.)
т. А – точка оптимального выбора производителя, при котором предприятие производит определенный объем продукции (Q = 20 в соответствии с графиком) и несет минимальный расходы на приобретение ресурсов туда и капитала