5.3.2. Поиск в глубину и итеративное углубление

Глубину вершины в корневом графе определим рекурсивно: глубина корня дерева равна нулю.

Глубина любой последующей вершины равна единице плюс глубина вершины, которая непосредственно ей предшествует.

Таким образом, вершиной, имеющей наибольшую глубину в дереве перебора, в данный момент служит та, которая должна в этот момент быть раскрыта. Стратегия поиска в глубину использует два списка вершин: отк (открыт- соответствует списку N в стратегии поиска с возвратами, реализован как стек) зак (закрыт- соответствует объединению списков C и T в стратегии поиска с возвратами) и определяется следующей последо­вательностью шагов:

1.Поместить начальную вершину в список, называемый отк.

2.Если список отк пуст, то на выход дается сигнал о неудаче поиска, в противном случае перейти к шагу (3).

3.Взять первую вершину из списка отк и перенести ее в список, называемый зак. Эту вершину назвать п.

4.Раскрыть вершину п, построив все непосредственно сле­ дующие за ней вершины. Поместить их (в произвольном по­ рядке) в начало списка отк и построить указатели, иду­ щие от них к вершине п.

5.Если одна из этих вершин целевая, то на выход выдать решение, просматривая для этого соответствующие указатели, в противном случае переходить к шагу 2. Соответствующая программа имеет вид.

Пример 5.3.2.

/*Программа: поиск в глубину*/

domains

s=symbol

l= s*

predicates

ap (l, l, l)

eq (l, l)

udob (l, l, l)

preemn (s, l)

gs(s)

solve (l, l, l) /*Первый аргумент- список отк, второй- зак */

sol

clauses

sol:-solve ([s], [], P), write (“sol =”,P),nl.

solve ([X|L1], M, P):- gs(X), P= [X|M].

solve ([X|N], M, P):- M1= [X|M], preemn (X, L), udob (L1, L, L2),

udob (M1, L2, L3), ap(L3, L1,L4), solve (L4,M1, P1), P=P1.

solve ([],M ,P):- P= resh.net, write(P),nl.

goal

sol

Если пространство состояний задачи является корневым деревом, то программа может быть упрощена, с учетом следующего. Чтобы найти путь решения Sol от заданной вершины S до некоторой целевой вершины, необходимо реализовать в программе следующие операции:

• если S— целевая вершина, то Sol = [S];

• иначе, если существует вершина- преемник V1 вершины V, такая, что имеется путь S1 от вершины V1 до целевой, то Sol = [V I S1].

Эта формулировка представляется следующей программой.

Пример 5.3.3.

/*Программа поиск в глубину 1*/

domains

s=symbol

l= s*

predicates

preemn (s, l)

gs(s)

solve (l, l, l)

sol

clauses

sol:- solve ([S], P), write(“Sol=”,P), nl.

solve(V, [V]):- gs(V).

solve(V,[V|P]):- preemn (V, [V1|N]), solve(V1, P).

solve(V, P):- preemn(V,[]), P=resh.net,write(P),nl.

goal

sol.

Программа представляет собой реализацию стратегии поиска в глу­бину на корневом дереве. Ее называют поиском в глубину потому, что программа ведет поиск, выбирая самую глубокую вершину для построения пути - ту, которая расположена дальше всех от начальной вершины. На рис. 5.10.показано, в каком порядке посещаются узлы. Этот порядок соот­ветствует трассировке выполнения программы при поиске цели sol.

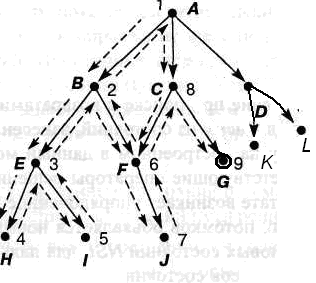
Рис.5.9. Схема поиска с возвратами

Рис.5.10. Схема поиска в глубину.

Поиск в глубину в наибольшей степени приемлем для рекурсивного стиля про­граммирования на языке Турбо- Пролог так как сама система при выполнении цели проверяет варианты по принципу поиска в глубину.

Поиск в глубину может привести к процессу, разворачивающемуся вдоль некоторого бесполезного пути, поэтому нужно ввести некоторую процедуру возвращения: после того как в ходе процесса строится вершина с глубиной, превышающей некоторую граничную глубину, раскрывается вершину наибольшей глубины, не превышающей этой границы, и т.д. При этом возникает оп­ределенное затруднение, связанное с тем, что подходящий предел необходимо уста­навливать заранее. Если этот предел будет установлен слишком низким (т.е. мень­шим по сравнению с длиной любого пути решения), поиск завершится неудачей. А если предел будет установлен слишком высоким, поиск потребует лишних затрат времени. Для преодоления этой сложности можно выполнять поиск в глубину итера­тивно, постепенно изменяя предел глубины, начиная с очень низкого предела глуби­ны и постепенно увеличивая этот предел до тех пор, пока не будет найдено решение. Этот метод называется итеративным углублением. Его можно реализовать путем модификации программы примера 5.3.2, введя параметр максимальной глубины.

Пример 5.3.4.

/*Программа: поиск в глубину*/

domains

s=symbol

l= s*

r= real

predicates

ap (l, l, l)

eq (l, l)

udob (l, l, l)

preemn (s, l)

gs(s)

solve (l, l, l, r, r)

sol

clauses

sol:-solve ([s], [], P,0,H), write (“sol =”,P),nl.

solve ([X|L1], M, P,Y,H):- gs (X), P= [X|M].

solve ([X|N], M, P,Y,H):- M1= [X|M], Y1= Y+1, Y1< H, preemn (X, L),

udob (L1, L, L2), udob (M1, L2, L3), ap(L3, L1,L4), solve (L4,M1, P1), P=P1.

solve ([X|N], M, P,Y,H):- N=[X1|N1], M1= [X1|M] , preemn (X1, L), udob (L1, L, L2), udob (M1, L2, L3), ap(L3, L1,L4), solve (L4,M1, P1), P=P1.

solve ([],M ,P):- P= resh.net, write(P),nl.

goal

sol

Параметр Н в этой программе представляет предельную глубину поиска.