14 Закон сохранения момента импульса
Распространим теперь это уравнение на систему МТ. Для этого напишем его для каждой точки, понимая под момент всех действующих на нее сил, как внутренних, так и внешних. Затем сложим все эти уравнения. При этом моменты внутренних сил исключатся. Силы действия и противодействия для каждой пары МТ направлены противоположно и направлены вдоль одной и той же прямой. Момент таких двух сил, а значит и моменты всех внутренних сил равны нулю. В результате получаем для суммарного момента импульса всех МТ системы
.
То есть мы получили уравнение для изменения момента импульса системы.
Если момент внешних сил относительно неподвижного начала равен нулю, то момент импульса относительно того же начала остается постоянным во времени. Это положение называется законом сохранения момента импульса. В частности, момент импульса сохраняется для изолированной системы МТ.
Если все силы, действующие на МТ, центральны, то момент импульса МТ относительно этого центра сохраняется. Однако, момент импульса относительно другого начала не сохраняется. Такое имеет место в нашей солнечной системе. Один из законов Кеплера фактически может быть переформулирован через закон сохранения момента импульса планеты при движении ее вокруг Солнца.
15 Работа и кинетическая энергия
Работой
силы
на
перемещении
выражается
формулой (см. рис.):
,
где
—
угол между векторами
и
Поскольку
перемещение
предполагается
бесконечно малым, величина
называется
элементарной работой. Если вспомнить
скалярное произведение, элементарная
работа может быть записана в виде:
.
В общем случае, когда МТ, двигаясь по криволинейной траектории, проходит путь конечной длины, этот путь можно разбить на бесконечно малые элементы, на каждом из которых сила может считаться постоянной, а элементарная работа записана вышеприведенной формуле. Если сложить все элементарные работы и перейти к пределу, то работа будет выражаться через криволинейный интеграл
,
где
обозначает
траекторию.
Единицей работы в системе СИ является джоуль (Дж). В системе СГС единицей работы является эрг. Легко показать, что
.
Работа, отнесенная к единице времени, т.е.
,
называется мощностью. Ее единицы — эрг/с и Дж/с, или ватт (Вт). Очевидно, что
.
Если
вспомнить, что
и
,
то формула работы принимает вид
.
Этот
интеграл в некоторых случаях легко
вычисляется. Если масса МТ постоянна,
то
и
интеграл преобразуется к виду:
,
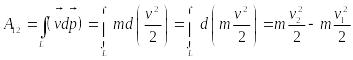где
—
начальная,
—
конечная скорость МТ. Величина
называется кинетической энергией МТ. Отсюда, работа равна
.
Таким образом, работа силы при перемещении МТ равна приращению кинетической энергии этой точки.
Также можно ввести кинетическую энергию системы МТ как сумму кинетических энергий МТ системы.
16 Консервативные и неконсервативные силы. Потенциальная энергия. Примеры потенциальной энергии.
Все силы в физике подразделяются на консервативные и неконсервативные.
Если силы взаимодействия зависят только от конфигурации МТ системы (т.е. их координат) и работа этих сил при перемещении системы из произвольного начального положения в произвольное конечное положение не зависит от пути перехода, а определяется только начальной и конечной конфигурациями системы, то такие силы называются консервативными.
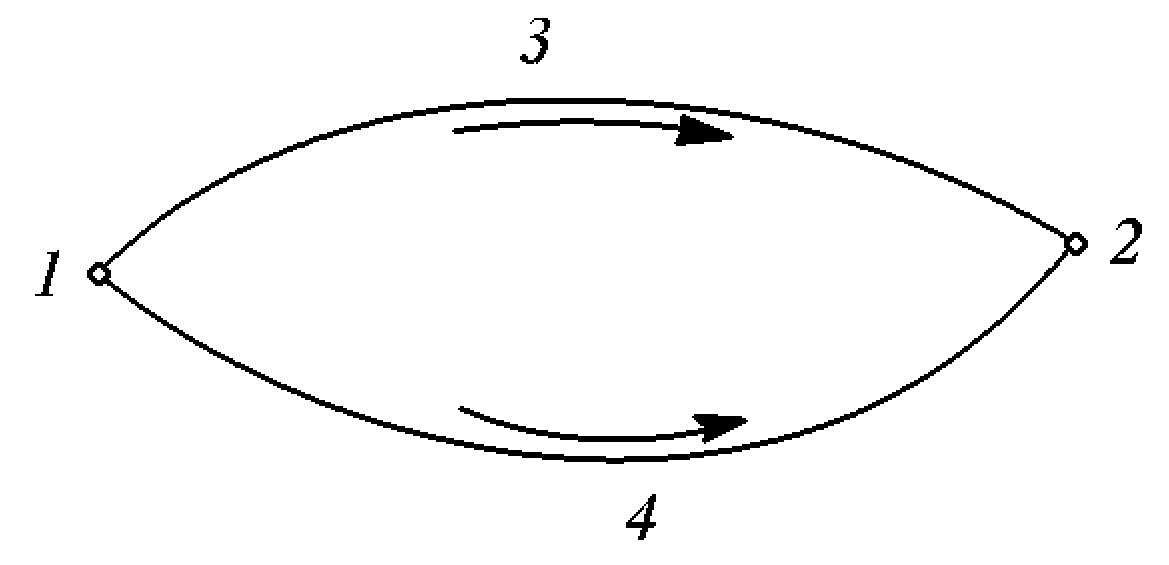
Для
консервативных сил выполняется следующее
свойство. Рассмотрим перемещение МТ из
точки 1 в точку 2 по двум путям: 123 и 142.
Так как силы консервативные, то работы
по этим двум траекториям равны:
.
Так кА силы зависят только от конфигурации,
то
,
где
—
работа, совершаемая при обратном движении
по пути 241. Отсюда следует, что
,
то есть работа по замкнутому пути равна
нулю. Свойство: работа консервативных
сил по любому замкнутому пути равна
нулю. К консервативным силам относятся
гравитационная сила, сила тяжести,
упругая сила, сила Кулона и многие
другие.
Все силы, не являющиеся консервативными, называются неконсервативными.
Если
на систему действуют только консервативные
силы, то для такой системы можно ввести
понятие потенциальной энергии. Примем
какое-либо произвольное положение
системы, характеризующееся заданием
координат ее МТ, условно за нулевое.
Работа, совершаемая консервативными
силами при переходе системы из
рассматриваемого положения в нулевое,
называется потенциальной энергией
системы в первом положении. Потенциальная
энергия системы
является
функцией только ее координат.
Нулевое положение произвольно. Поэтому потенциальная энергия меняется при изменении этого положения. Однако это не влияет на результаты вычислений. При изменении нулевого положения потенциальная энергия во всех точках поля сил меняется на одну и ту же постоянную, равную работе перехода из одной нулевой точки в другую. А в задаче всегда требуется работа при переходе из одной точки в другую, которая равна разности потенциальных энергий. То есть постоянная всегда вычитается и ответ не меняется.
Формула для работы консервативных сил выражается формулой
,
то есть всегда из потенциальной энергии начальной точки вычитается потенциальная энергия конечной точки.
Та
же работа может быть выражена через
кинетическую энергию. Приравнивая два
выражения, получаем
,
откуда
.
Сумма
кинетической и потенциальной энергий
системы называется полной энергией
системы
.
Таким образом,
,
или
.
В системе с одними консервативными силами полная энергия системы остается неизменной. Это положение называется законом сохранения механической энергии.
Приведем потенциальные энергии для некоторых сил.
1.
Сила тяжести.
.
Потенциальная энергия равна
.
Здесь
—
высота положения МТ,
—
произвольная константа. За нулевой
уровень можно принять произвольный
уровень, например уровень пола, уровень
моря и т.д.
можно
положить равной нулю.
2.
Потенциальна энергия растянутой пружины.
.
Эта сила совершает работу
.
Если упругую энергию пружины в недеформированном состоянии считать равной нулю, то
.
3. Потенциальная энергия гравитационного притяжения двух МТ.
.
Если выбрать потенциальную энергию в бесконечности равной нулю, то
.
Потенциальная энергия отрицательна.
Допустим
теперь, что в системе кроме консервативных
сил присутствуют неконсервативные,
которые называются еще диссипативными.
Тогда работа всех сил может быть разделена
на две части: консервативную
и
диссипативную
.
Первая часть выражается через разность
потенциальных энергий и вся работа
выражается через разность кинетических
энергий. Тогда
,
или
.
То есть в этом случае полная механическая энергия уменьшается.
Работа диссипативных сил переводит механическую энергию во внутреннюю тел, составляющих систему. На сегодняшний день считается, что если учесть все энергии, а не только механическую, то суммарная энергия сохраняется.