10 Неинерциальные системы отсчета. Силы инерции.

Неинерциальной системой отсчета называется система, которая движется  ускоренно относительно инерциальных систем.

Законы Ньютона выполняются в инерциальных системах отсчета. Запишем второй закон Ньютона в виде

.

Смысл индекса «абс» выяснится в дальнейшем. Для нахождения уравнений движения в неинерциальных системах отсчета необходимо установить законы преобразования сил и ускорений при переходе от инерциальной системы к любой неинерциальной системе отсчета. Ограничим рассмотрение малыми скоростями , т.е все скорости, в том числе и скорость системы отсчета, малы по сравнению со скоростью света в вакууме.

Условимся называть неподвижной произвольно выбранную инерциальную систему отсчета, а движение относительно нее — абсолютным. Именно только в этом смысле ускорение будет называться абсолютным. Абсолютное движение тела складывается из движения тела относительно рассматриваемой системы отсчета и движения системы отсчета относительно неподвижной системы отсчета. Первое называется относительным, второе – переносным.

Нашей целью является получить уравнение движения относительно любой системы отсчета. В инерциальной системе таким уравнением является уравнение второго закона Ньютона.

Возьмем две системы отсчета: неподвижную систему  с началом координат в точке  и движущуюся систему  с началом координат в точке . Пусть  — какая-либо МТ. Все необходимые векторы введены на рисунке. Векторы  в каждый момент времени связаны соотношением

Дважды дифференцируя это уравнение по времени, получим

Рассмотрим простейший случай, когда система  движется поступательно относительно неподвижной системы . Скорость  и ускорение  начала координат  системы  должны быть интерпретированы как переносные скорость и ускорение. Итак, при поступательном движении

,

Подставим теперь выражение для ускорения в закон Ньютона. Получим

.

Это и есть уравнение относительного движения МТ. Правая часть состоит из двух членов. Первый из них есть настоящая сила, которая не меняется при переходе из одной системы координат в другую, т.к. зависит от разности координат и разности скоростей действующих МТ. Второй член представляет из себя силу инерции, в этом случае поступательную. Эта сила меняется при переходе от одной неинерциальной системы отсчета к другой. Эта сила не подчиняется третьему закону Ньютона. Если считать, что все силы являются результатом взаимодействия тел, то силы инерции фиктивны.

Допустим теперь, что система отсчета  движется произвольно относительно неподвижной системы . Это движение можно разложить на поступательное со скоростью , равной скорости движения начала координат , и вращательное вокруг мгновенной оси, проходящей через это начало с угловой скоростью . Угловая скорость может меняться как по величине, так и по направлению. При вращении системы отсчета меняются не только проекции координат на оси вращающейся системы, а и направления единичных векторов в ней:

При каждом дифференцировании радиус-вектора по времени появляется дополнительный член, связанный с указанным эффектом. При этом из определения скорости (и ускорения) в системе отсчета следует:

Члены, получаемые из вращения ортов, в случае скорости должны быть отнесены к переносным величинам:

С ускорением несколько сложнее:

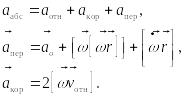
Вектор  зависит только от движения системы отсчета  относительно неподвижной системы . Слагаемое  зависит как от относительного, так и от переносного движений. Оно называется кориолисовым ускорением. Второй член в переносном ускорении известен как центростремительное ускорение и может быть преобразован к виду

,

где  — проекция радиус-вектора, перпендикулярная оси вращения. Последний член связан с неравномерностью вращения системы отсчета.

Уравнение для относительного движения выглядит так:

,

или более подробно

Все члены, стоящие справа, кроме , являются силами инерции.

Действие силы Кориолиса  видно из рисунка. При удалении МТ точки от центра вращения на МТ действует сила Кориолиса, заставляющая ее двигаться против вращения системы отсчета (рис. а). И для того, чтобы

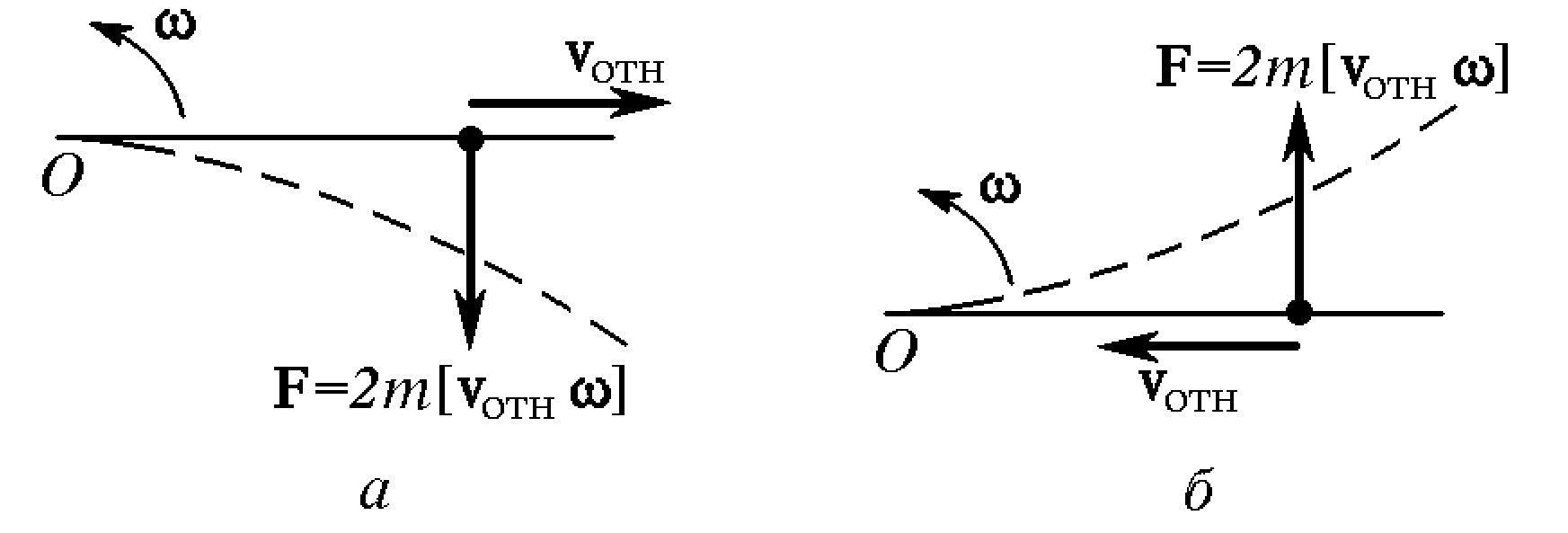
траектория МТ не изменилась, необходимо настоящая сила, действующая в сторону вращения. Физически МТ переходит от малого радиуса (и линейной скорости) к большим. Но движение самой МТ вдоль направления вращения имеет ту же линейную скорость, что и при малом радиусе. Поэтому она должна отстать. На рисунке б показано движение к центру вращения.

Принцип эквивалентности гравитационных сил и сил инерции.

 

Напомним, что все тела получают в данном гравитационном поле одинаковые ускорения. Все силы инерции пропорциональны массе МТ, на которую они действуют. Этот факт подвигнул А.Эйнштейна к идее замены гравитационного поля, действующего в данном месте на силу инерции. В этом и состоит принцип эквивалентности. Последовательное применение этого принципа привело к созданию общей теории относительности. Из уравнений ОТО получается расширение нашей вселенной и существование черных дыр. Из других следствий ОТО следует упомянуть смещение перигелия Меркурия и отклонение светового луча при его прохождении вблизи тяготеющего тела. Проверено астрономами.

Силы инерции

Сила инерции — фиктивная сила, которую можно ввести в неинерциальной системе отсчёта так, чтобы законы механики в ней совпадали с законами инерциальных систем.

 

В математических вычислениях введения этой силы происходит путём преобразования уравнения

 

F1+F2+…Fn = ma к виду

 

F1+F2+…Fn–ma = 0 Где Fn — реально действующая сила, а –ma — «сила инерции».

 

Закон инерции про инерционные системы отсчёта гласит, что без влияния неуравновешенных сил тело будет сохранять свою скорость или неподвижность. В качестве примера силы инерции можно рассмотреть простую силу инерции, которую можно ввести в равноускоренной системе отсчёта:

Пусть у нас есть быстро останавливающийся автобус. Все тела в нём будут нарушать закон инерции — они будут иметь тенденцию продолжать движение, и пассажирам придётся крепко держаться за поручни, чтобы не упасть вперёд, и оставаться неподвижными на своих местах относительно автобуса. Но если предположить, что всем пассажирам приходится противодействовать некой силе, то можно будет объяснить эту тенденцию её действием. Такую силу и назвали силой инерции. С введением этой силы закон инерции в автобусе восстановится — тела можно счесть подвергающимися действию этой силы, и тогда они будут вести себя в полном соответствии со вторым законом Ньютона. Т.е. если пассажиры приложат к себе относительно поручней дополнительную мускульную силу, противоположную силе инерции, то останутся на своих местах.

 

Среди сил инерции выделяют следующие:

простую силу инерции, которую мы только что рассмотрели;

центробежную силу, объясняющую стремление тел улететь от оси во вращающихся системах отсчёта;

силу Кориолиса, объясняющую стремление тел сойти с радиуса при радиальном движении во вращающихся системах отсчёта;