7 Третий закон Ньютона. Формулирование задачи движения материальных точек. Начальные условия.

Рассмотрим замкнутую систему, состоящую из двух взаимодействующих МТ. В этом случае справедлив закон сохранения импульса

Дифференцируя это уравнение по времени и использовав второй закон Ньютона, получим:

.

Где  и   — силы, с которыми рассматриваемые МТ действуют друг на друга. Привлечем опытный факт, согласно которому силы  и  направлены вдоль прямой, соединяющей взаимодействующие точки. Тогда мы приходим к третьему закону Ньютона:

Силы взаимодействия двух материальных точек равны по величине, противоположно направлены и действуют вдоль прямой, соединяющей эти материальные точки.

2. Аналогично, можно сформулировать третий закон Ньютона, если МТ много. Для этого рассматриваются отдельно силы взаимодействия отдельных точек друг с другом. Пусть  — сила, с которой i-я точка действует на k-ю,  — сила, с которой k-я точка действует на i-ю. Третий закон утверждает, что обе эти силы направлены вдоль прямой, соединяющей взаимодействующие точки, причем  .

3. Векторное уравнение движения МТ можно записать в координатной форме:

То есть получили три дифференциальных уравнения. Для их решения необходимо задать либо две векторные, либо шесть числовых постоянных. Обычно берут значения радиус-вектора  и скорости  в момент времени . Их называют начальными условиями.

Пример. Движение в поле силы тяжести.

Галилеем было установлено, что все тела в пустоте вблизи Земли падают с одинаковым ускорением. Сила тяжести выражается формулой , и уравнение движения переходит в

.

Простым дифференцированием можно убедиться, что это уравнение имеет общее решение:

при произвольных значениях постоянных векторов  и . Эти два вектора должны быть заданы при .

4. Для системы из  материальных точек необходимо задать начальный радиус-вектор и начальная скорость, т.е. всего  векторов или  чисел, определяющих начальные значения координат и скоростей материальных точек системы.

 

8,9 Силы в механике. Гравитационные силы. Закон всемирного тяготения. Принцип суперпозиции. Факты, подтверждающие закон всемирного тяготения. Сила упругости. Закон Гука. Сила трения. Сухое трение. Трение покоя. Трение скольжения.

1. Взаимодействие тел может происходить либо при непосредственном соприкосновении, либо на расстоянии. В первом случае взаимодействующие тела тянут или толкают друг друга. Возникающие при этом силы обычно вызываются деформациями тел. Если деформации малы, то от них можно отвлечься, учтя их влияние введением сил натяжения и давления.

2. Помимо сил, действующих при соприкосновении тел, в природе существуют силы, которые действуют на расстоянии, без участия промежуточной среды. К таким силам относятся гравитационные силы и силы взаимодействия наэлектризованных и намагниченных тел.

3. Согласно основным представлениям механики Ньютона силы, действующие на всякое тело в какой-либо момент времени, зависят от положения и скоростей остальных тел в тот же самый момент времени. Такое представление приводит к бесконечно большой скорости передачи взаимодействий. Опытные же факты привели к заключению, что скорость передачи взаимодействий ограничена скоростью света в вакууме. Отсюда сразу следует, что третий закон Ньютона не выполняется для взаимодействий на расстоянии. Физики нашли выход из этого. Они введи понятие поля. Тело  возбуждают в окружающем пространстве силовое поле, которое в месте нахождения тела  проявляется в виде действующих на него сил. И обратно. Взаимодействия прикосновением являются частными случаями полевого взаимодействия — через молекулярные поля.

4. Сила упругости.

Силами упругости называются силы, возникающие при деформации тел, то есть при изменении их формы и размеров. При этом изменяются расстояния между молекулами внутри тела, и электромагнитные силы пытаются вернуть молекулы обратно. Если после прекращения действия силы, вызвавшей деформацию, тело принимает первоначальную форму и размеры, то деформация называется упругой.

Простейшими деформациями являются деформации растяжения и сжатия. Они описываются законом Гука при малых упругих деформациях.

На рисунке рассмотрен случай растяжения. Сила, вызывающая растяжения стержня обозначена . Равная ей по величине и противоположно направленная возвращающая сила выражается через экспериментальный закон Гука:

.

Здесь  - размер, на который увеличилась длина стержня, а  называется коэффициентом жесткости стержня. Знак минус указывает на то, что сила направлена в сторону, обратную изменения длины стержня. Если разделить силу на площадь сечения стержня , а удлинение  на первоначальную длину стержня , то закон Гука преобразуется к виду:

.

Здесь  называется модулем Юнга и зависит только от вещества стержня. Для конкретного стержня величина  выражается из формулы

.

Аналогично представляется другая деформация — сдвига. Ее мы рассматривать не будем. Все малые деформации сводятся к деформациям растяжения и сдвига.

5. Гравитационная сила. Сила тяжести.

Исаак Ньютон воспользовался тремя законами астронома Иоганна Кеплера и вывел закон всемирного тяготения, выражающийся формулой:

.

Здесь  и  — массы взаимодействующих материальных точек,  — расстояние между точками,  — сила взаимодействия,  — гравитационная постоянная. Сила направлена по прямой, соединяющей МТ и является силой притяжения. В настоящее время этот закон обобщен в общей теории относительности. Как объясняется эта формула изнутри, пока не известно. За последние несколько лет выяснилось, что возможно существует темная материя, в которой предполагается гравитационная сила отталкивания.

Вблизи планеты, в том числе вблизи Земли ( ), эта формула преобразуется к виду:

,

где  называется ускорением свободного падения. Эта сила обычно называется силой тяжести.

Силы трения.

Силы трения действует на поверхности между движущимися телами. Различают сухое трение между твердыми телами и внутреннее трение между отдельными слоями одной и той же жидкости.

Сейчас рассмотрим сухое трение, которое в свою очередь подразделяется на трение скольжения и трение качение. Ограничимся трением скольжения, которое представлено на рисунке. Тело  расположено поверх тела . Рассмотрим силы, действующие на тело .  — вес тела,  — сила реакции опоры,  — сила, толкающая тело вправо,  — сила трения скольжения.

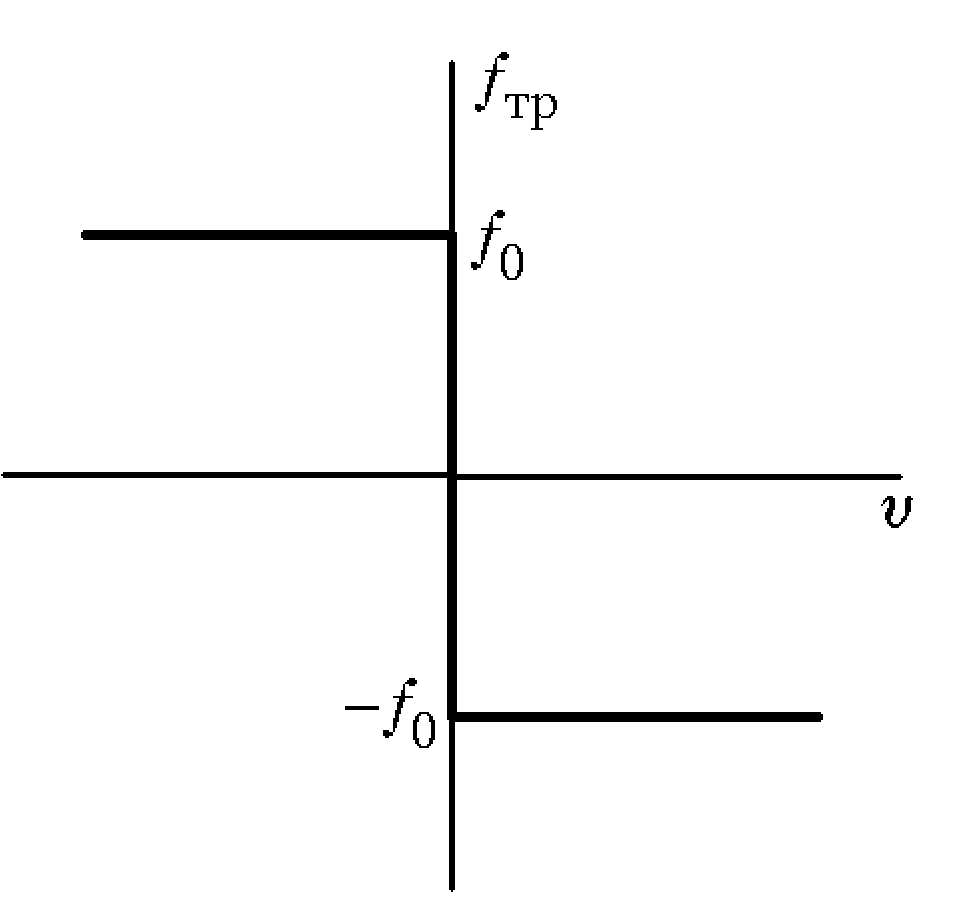
В состоянии покоя вес и реакция опоры уравновешены. Если приложить силу , то при небольших ее величинах тело будет неподвижно, то есть сила трения равна по величине этой силе. Такая сила трения называется силой трения покоя. Но она не может быть больше некоторой опытной величины . Для этой величины установлено, что , где  — коэффициент трения. Определяется материалами тел. Приближенная зависимость силы трения от скорости движения верхнего тела относительно нижнего представлено на рисунке.

Сила внутреннего трения будет рассмотрена в другом месте.