
- •1 Кинематика материальной точки. Тело отсчета. Прямолинейное движение. Движение тела в пространстве. Декартова система координат. Система отсчета.
- •2 Радиус-вектор, скорость и ускорение материальной точки, их связь с декартовыми координатами.
- •3 Движение по криволинейной траектории. Тангенциальное и нормальное ускорения.
- •4 Кинематика твердого тела. Поступательное движение твердого тела. Вращение тела вокруг неподвижной оси. Угловая скорость вращения. Вектор угловой скорости. Угловое ускорение.
- •5 Первый закон Ньютона – закон инерции. Инерциальная система отсчета.
- •7 Третий закон Ньютона. Формулирование задачи движения материальных точек. Начальные условия.
- •10 Неинерциальные системы отсчета. Силы инерции.
- •11 Замкнутая система. Законы сохранения. Связь законов сохранения со свойствами пространства и времени.
- •12 Закон сохранения импульса
- •13 Момент силы и момент импульса относительно неподвижного начала. Их связь.
- •14 Закон сохранения момента импульса
- •15 Работа и кинетическая энергия
- •16 Консервативные и неконсервативные силы. Потенциальная энергия. Примеры потенциальной энергии.
- •17 Закон сохранения и изменения механической энергии
- •18 Абсолютно неупругий и абсолютно упругий удары.
- •19 Механика абсолютно твердого тела. Вращение вокруг неподвижной оси. Момент инерции.
- •20 Теорема Гюйгенса-Штейнера. Вычисление моментов инерции. Примеры.
- •21 Колебания. Разные типы колебаний.
- •22 Гармонические колебания. Основные характеристики колебательного процесса. Дифференциальное уравнение гармонических колебаний.
- •23 Пружинный маятник. Энергия маятника.
- •24 Физический маятник.
- •25 Затухающие колебания. Дифференциальное уравнение, вид решения, график,
- •26 Вынужденные колебания. Резонанс.
- •27 Волновые процессы. Уравнение плоской волны. Дифференциальное уравнение плоской волны.
- •28 Макроскопическая система большого количества молекул. Ее параметры. Равновесная система.
- •29 Массы и размеры молекул. Атомная масса. Молярная масса.
- •30 Уравнение идеального газа.
- •31 Распределение молекул по скоростям в идеальном газе.
- •32 Газ во внешнем потенциальном поле. Распределение Больцмана. Барометрическая формула.
- •33 Степени свободы. Теорема о равнораспределении энергии по степеням свободы.
- •34 Теплопередача. Макроскопическая работа. Первый закон (начало) термодинамики. Применение к изопроцессам.
- •35 Явления переноса. Средняя длина свободного пробега.
- •36 Диффузия.
- •37 Теплопроводность.
- •38 Взаимодействие зарядов. Их знаки. Единичный заряд. Закон Кулона.
- •39 Напряженность электростатического поля. Определение. Напряженность точечного заряда. Силовые линии.
- •41 Электрический диполь. Дипольный момент. Напряженность диполя на больших расстояниях.
- •41 Поток вектора и теорема Гаусса.
- •42,43 Потенциал электростатического поля. Потенциал точечного заряда. Консервативность электростатического поля
- •44 Проводники в электрическом поле.
- •45 Поляризация диэлектриков. Поляризуемость. Вектор электрического смещения. Электрическая проницаемость.
- •46 Электрический ток. Вектор плотности тока. Закон сохранения заряда в интегральном и дифференциальном виде.
- •47 Закон Ома в дифференциальном и интегральном виде. Удельная проводимость и удельное сопротивление.
- •48 Действие магнитного поля на проводники с током и движущиеся заряды.
- •49 Магнитное поле равномерно движущегося заряда. Закон Био—Савара.
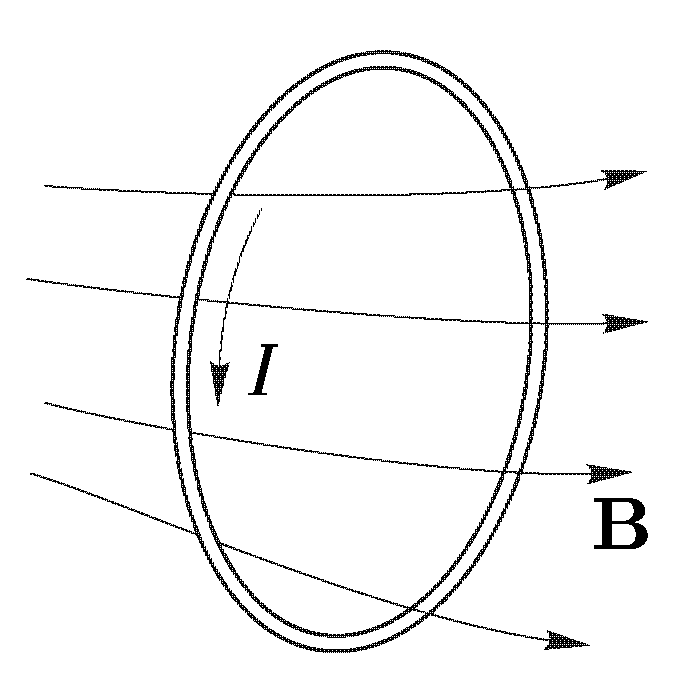
- •50 Магнитное поле бесконечного прямого провода и витка с током.
- •51 Теорема Гаусса для магнитного поля. Циркуляция магнитного поля.
- •52 Магнитное поле в веществе. Различные типы магнетиков.
- •53 Емкость проводников и конденсаторов. Емкость шарового конденсатора.
- •54 Энергия заряженного конденсатора. Плотность электрической энергии. Энергия системы заряженных тел.
- •55 Электромагнитная индукция
- •56 Магнитный поток
- •57 Работа при перемещении витка с током в постоянном магнитном поле.
- •58 Самоиндукция. Коэффициенты индуктивности.
- •59 Энергия магнитного поля.
- •60 Ток смещения.
- •61 Система уравнений Максвелла.
- •62 Следствия из уравнений Максвелла.
- •63 Электромагнитные волны.
58 Самоиндукция. Коэффициенты индуктивности.
Мы знаем, что всякий ток в проводнике создает магнитное поле. Но это поле, начав изменяться, в свою очередь влияет на вызвавший его ток. Это явление называется самоиндукцией.
Если в пространстве нет ферромагнетиков, то магнитный поток через виток с током пропорционален протекающему в нем току носит название коэффициента самоиндукции провода. Он зависит только размеров и конфигурации проводника. Тогда закон электромагнитной индукции будет следующим
![]()
.
![]() .
.
Для длинного соленоида вычисляется и равно
![]() ,
где
—
плотность витков на единицу длины, а
,
где
—
плотность витков на единицу длины, а
![]() —
объем пространства внутри соленоида.
—
объем пространства внутри соленоида.
В
системе СИ единицей измерения коэффициента
самоиндукции является Гн (генри,
![]() ).
).
Если рядом расположенных проводников с токами много, то кроме коэффициентов самоиндукции вводятся коэффициенты взаимной индукции, которые описывают часть ЭДС индукции, возникающей под воздействием другого тока
![]() .
.
Коэффициенты взаимной индукции также измеряются в Гн.
59 Энергия магнитного поля.
Вычисление энергии проводника приводит к формуле
![]() .
.
В случае длинного соленоида эта формула преобразуется к
![]() .
.
Отсюда
легко получить плотность энергии
магнитного поля (![]() )
)
![]() .
.
Эта формула годится при любой конфигурации магнитного поля.
60 Ток смещения.
Начнем с теоремы о циркуляции магнитного поля:
![]() .
.
означает алгебраическую сумму всех токов, пронизывающих поверхность, ограниченную контуром . Это уравнение может быть переписано в дифференциальном виде:
, |
(1) |
где — вектор плотности тока. Как мы сейчас увидим, это уравнение не полно. Вспомним, что закон сохранения электрического заряда в дифференциальной форме выглядит так:
![]() .
.
Теперь применим оператор дивергенции к уравнению (1). Так как всегда дивергенция, примененная к ротору, дает нуль, то получается:
![]() .
.
Такой вариант закона сохранения заряда получается только в случае, когда плотность заряда не зависит от времени, т.е. задача стационарна. Но уравнения электромагнитного поля должны выполняться и для переменных полей. Следовательно, к правой части уравнения (1) надо добавить член, чтобы дивергенция от правой части всегда обращалась в нуль.
Такой член можно получить, воспользовавшись теоремой Гаусса для вектора смещения электрического поля:
![]() .
.
Эта
формула получена из известной вам
теоремы Гаусса умножением на
![]() (
в
вакууме), заменой вектора напряженности
электрического поля на вектор смещения
и обозначением алгебраической суммы
всех зарядов внутри объема, ограниченного
замкнутой поверхностью
,
через
.
В дифференциальном виде это уравнение
выглядит так:
(
в
вакууме), заменой вектора напряженности
электрического поля на вектор смещения
и обозначением алгебраической суммы
всех зарядов внутри объема, ограниченного
замкнутой поверхностью
,
через
.
В дифференциальном виде это уравнение
выглядит так:
![]() .
.
Дифференцируя это соотношение по времени, получаем:
![]() .
.
Точка над вектором смещения означает производную по времени.
Пользуясь теперь уравнением закона сохранения заряда, получаем:
![]() ,
,
то
есть производная по времени от вектора
смещения должна быть добавлена в теорему
циркуляции магнитного поля. Максвелл
назвал этот член плотностью тока смещения
![]() ,
а сумму обычного тока и тока смещения
полным током. Конечно ток смещения
никакой не ток, но ведет себя подобно
ему в нестационарных задачах.
,
а сумму обычного тока и тока смещения
полным током. Конечно ток смещения
никакой не ток, но ведет себя подобно
ему в нестационарных задачах.
Окончательно
|
(2) |
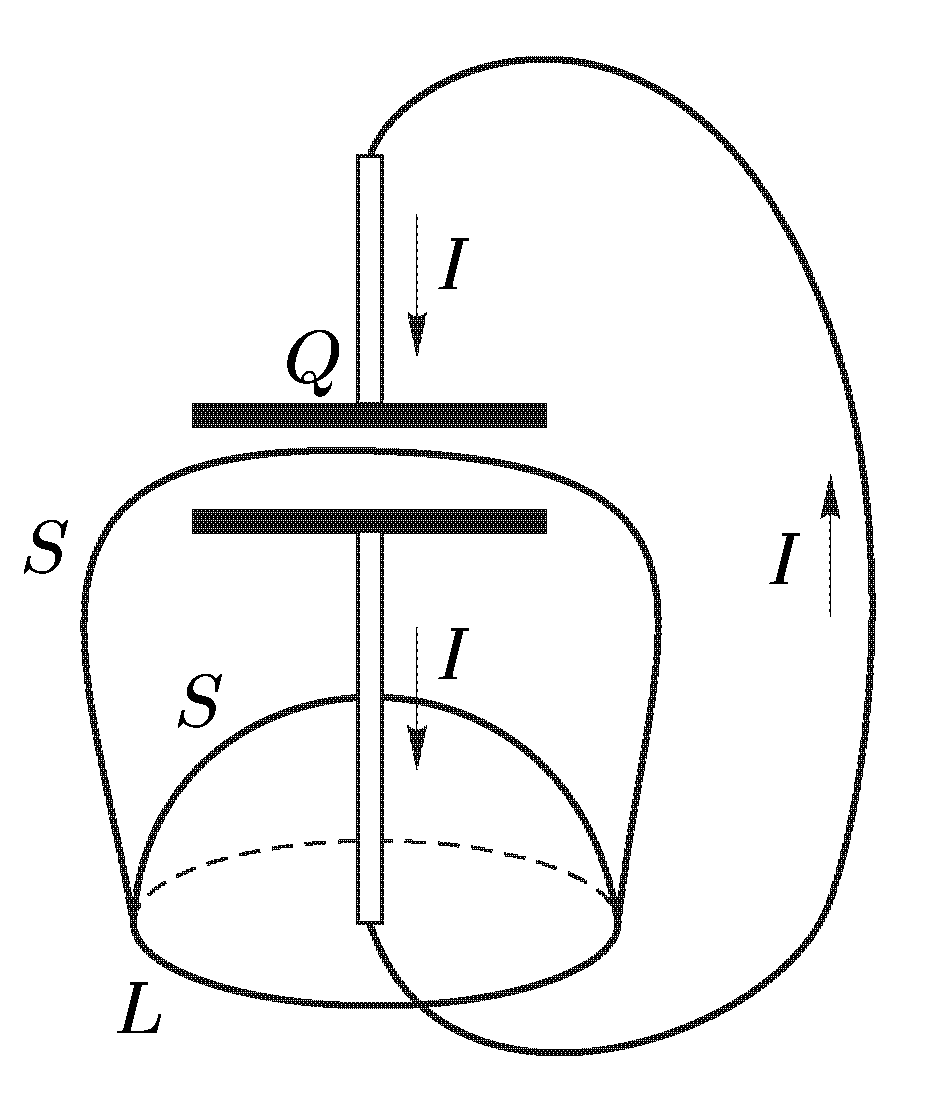
Уравнение (2) является одним из уравнением Максвелла.
Вопрос: а действительно ли существует такой ток смещения. Ответ: результат Максвелла давно подтвержден на эксперименте. На рисунке справа представлен один из таких экспериментов. На нем нарисован конденсатор, присоединенный к цепи переменного тока. В случае переменного тока в промежутке между обкладками электрическое поле становится переменным и там же возникает магнитное поле, которого в электростатике не наблюдается.
То есть Максвелл (теоретик) открыл, что изменение электрического поля создает магнитное поле. Аналогично закону электромагнитной индукции.
