56 Магнитный поток
После предварительного рассмотрения сформулируем закон в общем виде. Как и в случае электрического поля можно ввести поток индукции магнитного поля:
.
Здесь
—
площадь контура, через который проходит
магнитное поле,
—
нормаль к площадке, ограниченной
контуром. Скалярное произведение
может
быть заменено на
,
где
—
угол между направлениями вектора
индукции и нормалью. Если магнитная
индукция меняется по величине и
направлению, то формула для потока
переходит в следующую
.
И напоминаю теорему Гаусса для магнитного потока:
.
Необходимо
отметить, что поверхность, на которой
вычисляется поток индукции, можно
деформировать. Для доказательства
рассмотрим рисунок справа. На нем
представлен разрез контура (точки
и
)
и разрез двух поверхностей
(кривые
и
).
Крест в точке
и
точка — в
показывают
направление обхода контура, которое
связано правым винтом с направлением
нормалей на поверхности. Так как поток
вектора индукции через замкнутую
поверхность равен нулю, то потоки по
отдельным поверхностям
и
равны
между собой (с учетом направления
векторов нормали). Отсюда следует, что
поверхность
можно
деформировать как угодно.
57 Работа при перемещении витка с током в постоянном магнитном поле.
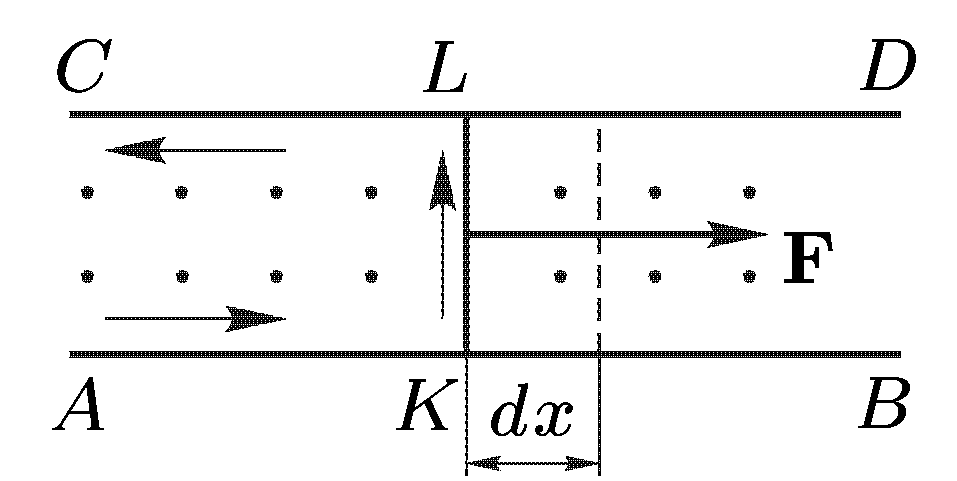
Рассмотрим
сначала частный случай. Пусть параллельные
проводники
и
(см.
рис.) помещены в однородное постоянное
магнитное поле, перпендикулярное к
плоскости рисунка и направленное к нам.
Слева находится источник тока, не
показанный на рисунке. По проводам может
свободно перемещаться проводящий мостик
,
замыкающий ток
,
текущий по проводам левее мостика. Если
—
длина мостика, то на него магнитное поле
действует с силой
.
При перемещении мостика на
эта
сила совершает работу
,
где
—
площадь прямоугольника
.
Величина
есть
магнитный поток через тот же прямоугольник.
Обозначив его через
,
получим для элементарной работы
,
а для конечной работы
.
Таким образом, работа, совершаемая магнитным полем над током, равна приращению магнитного потока, умноженного на ток. При выводе предполагалось, что ток при перемещении мостика поддерживается постоянным.
Результат
справедлив и при произвольном направлении
магнитного поля. Чтобы убедится в этом,
разложим вектор
на
три составляющие:
.
Составляющая вдоль мостика
параллельна
току в нем и не оказывает на мостик
силового воздействия. Составляющая
вдоль
перемещения дает силу, перпендикулярную
к перемещению и работы не производит.
Работа производится лишь составляющей
,
перпендикулярной к плоскости рисунка,
в которой перемещается мостик
.
Докажем теперь, что полученные формулы справедливы для любого витка с током при произвольном перемещении его в постоянном неоднородном магнитном поле. Виток может не только перемещаться, но и произвольно деформироваться. Для доказательства достаточно мысленно разбить виток на бесконечно малые элементы тока и рассмотреть бесконечно малые перемещения их. При бесконечно малом перемещении элемента тока магнитное поле, в котором он перемещается, может считаться однородным. Суммируя перемещения всех малых элементов, получаем выражение для элементарной работы. Интегрируя затем, получаем вновь выражение для конечной работы. Необходимо подчеркнуть, что ток в витке должен поддерживаться постоянным.
Если в магнитном поле перемещается катушка с намотанным на нее многократно проводом, то в работе по ее перемещению необходимо учесть перемещение каждого витка. И тогда в окончательном выражении работы будет вместо магнитного потока стоять сумма магнитных потоков через все витки
.
Величина
носит
название потокосцепления. Если все
потоки одинаковы, то
,
где — число витков катушки, а работа по перемещению катушки суть
.