51 Теорема Гаусса для магнитного поля. Циркуляция магнитного поля.
Теорема Гаусса для магнитного поля выглядит очень просто:
,
или в дифференциальной форме
.
Эти уравнения интерпретируются как отсутствие магнитных зарядов. Экспериментально эти заряды не найдены.
Циркуляция вектора (см. рисунок) выражается формулой
,
где
сумма справа распространяется на все
токи, которое пересекают площадку,
ограниченную контуром. Токи входят со
своими знаками, Положительный ток
образует правый винт с направлением
обхода контура, а отрицательный — левый
винт. Для варианта на рисунке сумма
справа выглядит как
.
Ток
не
входит в сумму, так как не пересекает
площадку.
В дифференциальной форме циркуляция ожжет быть представлена в виде
,
где левая часть формулы есть
.
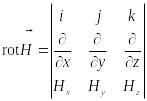Циркуляция может быть использована для вычисления магнитного поля в соленоиде:
,
где — число витков на единицу длины соленоида.
52 Магнитное поле в веществе. Различные типы магнетиков.
Внутри вещества все токи являются замкнутыми (движение электронов в атомах и молекулах) и образуют отдельные контуры. Каждый контур обладает своим магнитным моментом. Для характеристики магнитных свойств вещества вводится понятие намагниченности. Намагниченностью называется вектор, равный магнитному моменту единицы объема вещества, то есть
,
где — число молекул в малом объеме . При малых значениях внешнего магнитного поля вектор намагниченности линейно зависит от напряженности магнитного поля и в случае однородного вещества равна
,
где
—
магнитная восприимчивость. Общее
магнитное поле складывается из внешнего
и
поля создаваемого токами внутри вещества
:
,
или
.
Для однородной среды:
.
Здесь введен новый коэффициент , называемый относительной магнитной проницаемостью вещества.
Различные типы магнетиков.
Все вещества являются магнетиками, т.е. подвержены влиянию магнитного поля.
Они подразделяются, во-первых, на слабомагнитные, у которых близок к единице и сильномагнитные, у которых он может быть очень большим.
Слабомагнитные вещества в свою очередь делятся на парамагнетики, у которых чуть больше единицы и диамагнетики, у которых меньше единицы.
Сильномагнитные вещества не только обладают порядка 1000, но и имеют сложную зависимость магнитной индукции от внешнего магнитного поля, называемой гистерезисом. Делятся они на ферромагнетики, ферримагнетики, антиферромагнетики и геликоидальные магнетики.
53 Емкость проводников и конденсаторов. Емкость шарового конденсатора.
Как мы знаем, заряженный уединенный проводник имеет одинаковый потенциал в каждой своей точке. Потенциал создаваемого им электрического поля на бесконечности условимся считать равным нулю. Если удвоить заряд проводника, то его потенциал также удвоится. Между зарядом проводника и его потенциалом существует прямая пропорциональность:
.
Коэффициент
зависит
только от размеров и формы проводника,
а также от диэлектрической проницаемости
окружающего диэлектрика и ее распределения
в пространстве. Он называется емкостью
уединенного проводника. Например, для
шара радиусом
в
одиночном диэлектрике
,
и поэтому
.
Рассмотрим
прибор, называемый конденсатором. Всякий
конденсатор состоит из двух металлических
пластин, между которыми расположен слой
диэлектрика. Обычно на одной из пластин
помещается положительный заряд, а на
другой — такой же по величине отрицательный.
Кроме этого размеры пластин должны быть
много больше расстояния между ними. В
этом случае электрическое поле практически
сконцентрировано только между пластинами.
Пусть
—
заряд положительной пластины,
—
разность потенциалов между пластинами,
тогда
.
Постоянная зависит только от размеров и устройства конденсатора и называется емкостью (электроемкостью) конденсатора. Кроме этого, емкость кондесатора зависит от диэлектрической проницаемости диэлектрика, помещенного между пластинами.
Интересным
моментом является то, сто наилучшим
диэлектриком с
был
бы проводник, если бы он не проводил
электрический ток. Однако инженеры
нашли выход, создав электролитические
конденсаторы. У них между пластинами
заливают электролит (проводник), а затем
пропускают в одном направлении
электрический ток. При этом на одной из
пластин осаждается очень тонкая
диэлектрическая пленка. Такие конденсаторы
имеют самые большие емкости.
Единицей измерения емкости в системе СИ является фарад (Ф).
Емкостью
в 1 фарад обладает уединенный шар в
вакууме с радиусом
,
т.е больше радиуса Земного шара. Обычно
используют пФ и мкФ.
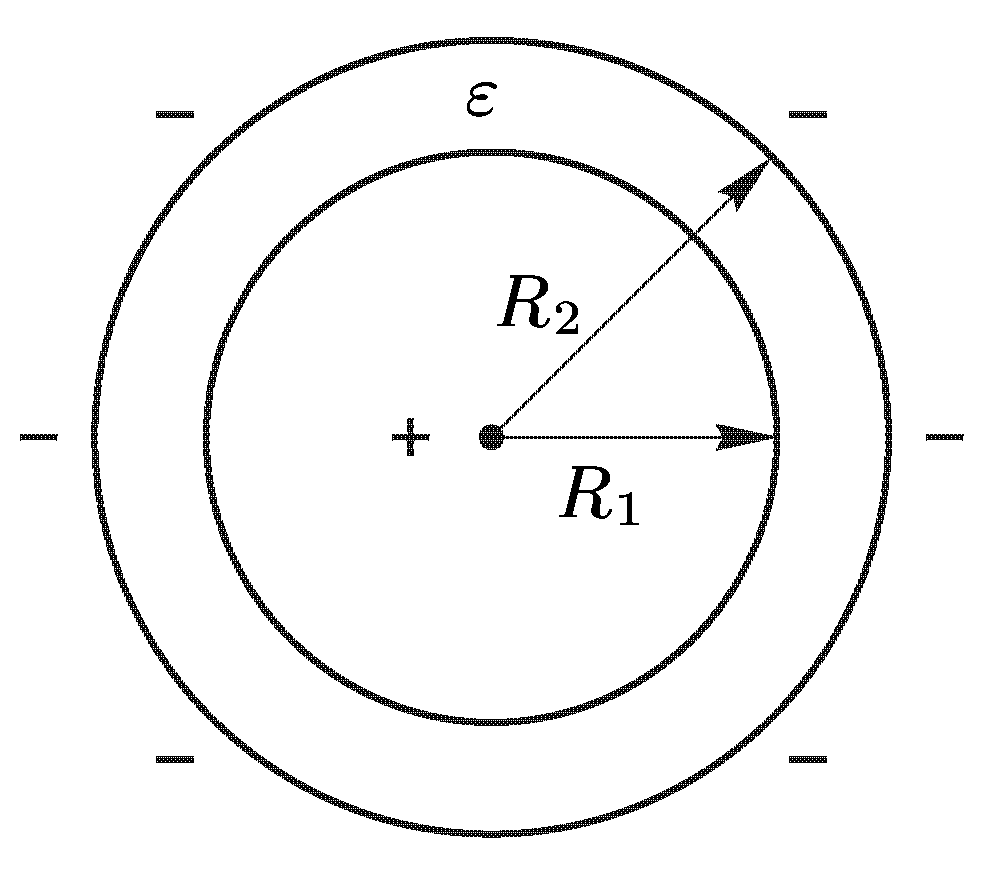
Емкость
шарового конденсатора. Обкладками
конденсатора являются две сферы:
внутренняя с радиусом
и
внешняя с радиусом
(см.
рис.). Разность потенциалов между ними
.
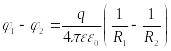Емкость конденсатора
.
Если
толщина зазора между обкладками
мала
по сравнению с радиусами
и
,
то площади обкладок почти одинаковы и
приближенно равны
.
Тогда
,
то есть совпадает с емкостью плоского конденсатора. Формула последнего выводится просто и мы не будем приводить ее вывод.
Существуют еще цилиндрические конденсаторы Пусть и — радиусы внутренней и внешней обкладок, а — длина конденсатора (см. рис.). Тогда при пренебрежении краевыми эффектами получаем
.
Эта формула при малом зазоре также переходит в формулу для плоского конденсатора.
Когда заряженных тел не одно, то можно показать, что заряды этих тел являются линейными однородными функциями их потенциалов и обратно. То есть можно записать формулу
.
Постоянные
называются
емкостными коэффициентами.