46 Электрический ток. Вектор плотности тока. Закон сохранения заряда в интегральном и дифференциальном виде.

Электрический ток.

Сторонние силы. Закон Ома для контура и его части. Представление о сторонних силах. Условие протекания стационарных токов. Электродвижущая сила (Э.Д.С.). Закон Ома для участка цепи и для контура.

 

Электрический ток есть упорядоченное движение электрических зарядов. Носителями зарядов могут быть электроны (проводники и полупроводники), в электролитах и ионизированных газах положительные и отрицательные ионы, в плазме — электроны и ядра.

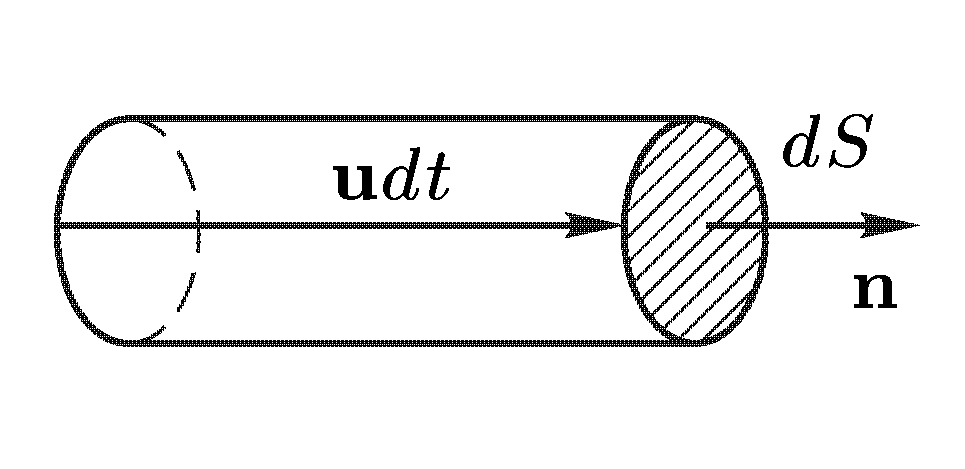
Рассмотрим простейший случай, когда все носители заряда одинаковы. Выделим в среде, по которой течет ток, произвольный бесконечно малый объем и обозначим через  средний вектор скорости рассматриваемых носителей в этом объеме. Его называют дрейфовой скоростью движения носителей заряда. Обозначим через  концентрацию носителей, т.е. их число в единице объема. Проведем бесконечно малую площадку , перпендикулярную к скорости . Построим на ней бесконечно короткий прямой цилиндр с высотой  (см. рис.). Все частицы, заключенные внутри этого цилиндра, за время  пройдут через площадку , перенося через нее в направлении скорости  электрический заряд , где  — заряд одной частицы. Через единицу площади за единицу времени переносится электрический заряд . Вектор

называется плотностью электрического тока. Направление вектора совпадает с направлением упорядоченного течения положительного электричества.

В случае нескольких типов зарядов, создающих ток, плотность тока определяется выражением

,

где  — номер носителя.

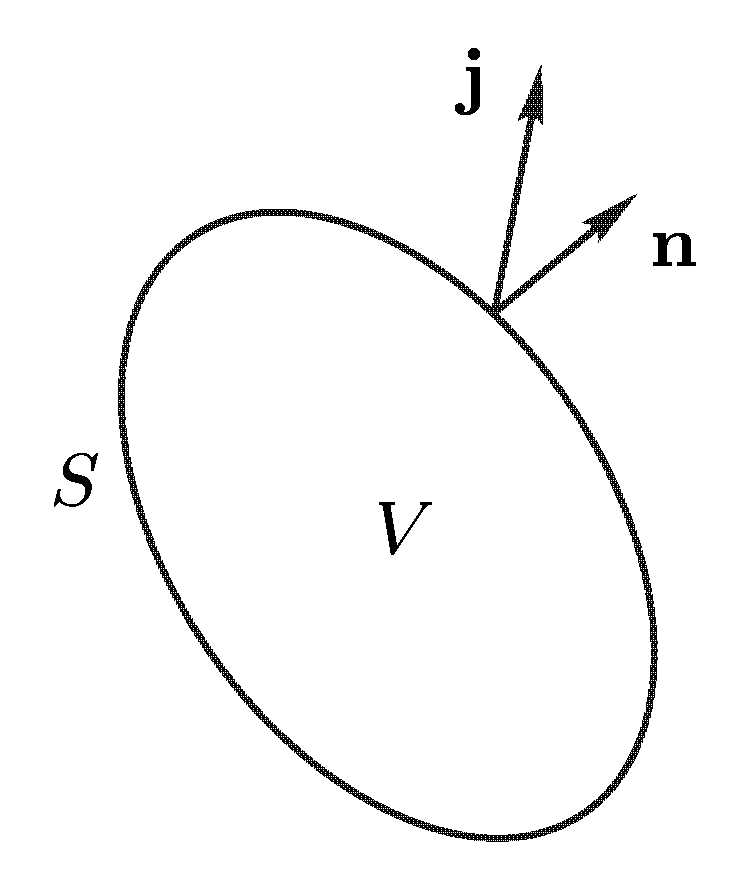
Теперь можно сформулировать закон сохранения электрического заряда. Пусть  — плотность заряда и  — вектор плотности тока. Возьмем в среде произвольную замкнутую поверхность , ограничивающую объем  (см. рис.). Количество заряда, ежесекундно вытекающее из объема  через поверхность , представляется интегралом . (Здесь  — проекция на внешнюю нормаль вектора .) Ту же величину можно представить в виде ,  — заряд, содержащийся в объеме . Выражая заряд через интеграл от плотности и приравнивая оба выражения, получаем соотношение

.

Поверхность неподвижна. После преобразований можно получить дифференциальное уравнение

.

Обе эти формулы выражают закон сохранения заряда в макроскопической электродинамике. ( ). Когда токи стационарны, т.е. не зависят от времени, то члены с производной по времени обращаются в нуль.

 

47 Закон Ома в дифференциальном и интегральном виде. Удельная проводимость и удельное сопротивление.

Одним из способов возбуждения электрического тока является создание и поддержание в них электрического поля. Как показывает опыт, для многих тел в широких пределах плотность электрического тока  пропорциональна напряженности электрического поля :

,

где  (иногда обозначается )— постоянная для данного металла величина, называемая его удельной электрической проводимостью. Этот закон носит название закона Ома. Величина удельной проводимости зависит от температуры, давления и пр.  Величина, обратная , называется удельным сопротивлением материала.

.

Если выбрать однородный проводник длины  и площадью сечения  и  перейти к величинам тока  и разности потенциалов, приложенной к концам проводника , то получим соотношение:

,

где величина  называется сопротивлением введенного выше проводника. Последнее уравнение носит название закона Ома в интегральной форме. Он выполняется для участка цепи.

Если предоставить проводник сам себе, то через некоторое довольно быстрое время ток прекратится. Этот вариант мы изучали в электростатике. Для постоянного поддержания тока необходимо, чтобы заряды, дошедшие до конца проводника возвращались к его началу. Это делается при помощи сторонних сил, роль которых выполняют различные устройства, в том числе генераторы тока на электростанциях, химические элементы и пр. Для их учета в уравнение закона Ома вводится дополнительную напряженность, . После интегрирования по проводнику получаем электродвижущую силу. И тогда уравнение закона Ома в интегральной форме выглядит так:

.

Здесь  обозначает сопротивление всей цепи. Полное сопротивление складывается из сопротивления внешней цепи  и сопротивления источника тока .