45 Поляризация диэлектриков. Поляризуемость. Вектор электрического смещения. Электрическая проницаемость.

Диэлектрики не проводят электричество. Электроны внутри них не являются свободными. Однако индукционные заряды возбуждаются.

Заряды в диэлектрике могут смещаться из своих положений равновесия лишь на малые расстояния, порядка атомных. Под действием приложенного электрического поля центр тяжести электронов в молекуле немного смещается относительно центра тяжести атомных ядер. Молекулы становятся электрическими диполями, ориентированными положительно заряженными концами в направлении электрического поля . Диэлектрик становится поляризованным. 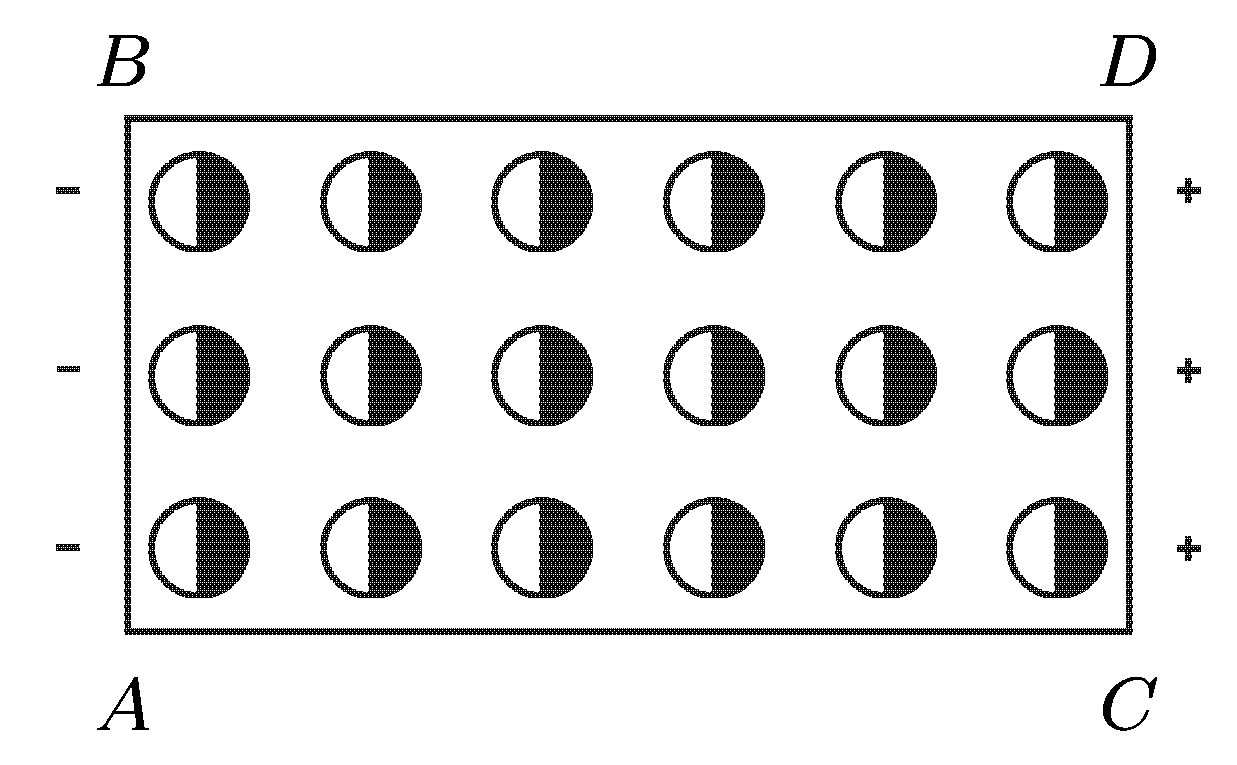На схематическом рисунке диэлектрик изображен в виде прямоугольного параллелепипеда, а молекулы — в виде шариков. Положительно заряженная половина молекулы закрашена в черный цвет, отрицательно заряженная оставлена светлой. Видно, что на конце  параллелепипеда выступают некомпенсированные отрицательные, а на конце  — положительные поверхностные заряды. Их называют поляризационными, или связанными, зарядами. В объеме диэлектрика происходит компенсация положительных и отрицательных зарядов молекул, и никаких макроскопических поляризационных зарядов не появляется. Однако это справедливо только тогда, когда поляризация диэлектрика однородна, т.е. когда все молекулы диэлектрика поляризованы и ориентированы одинаково. В случае неоднородности могут появиться объемные поляризационные заряды.

Помимо электрически нейтральных молекул в диэлектрике могут существовать положительные или отрицательно заряженные ионы, возникающие, например, при электризации трением. Такие заряды называются свободными.

Механизм поляризации диэлектрика может быть и иным. Существуют диэлектрики, молекулы которых обладают дипольными моментами уже в отсутствие электрического поля. Такие молекулы называются полярными. Если поля нет, то полярные молекулы совершают хаотические тепловые движения и ориентированы беспорядочно. При наложении электрического поля дипольные моменты молекул ориентируются преимущественно в направлении поля. Диэлектрик становится поляризованным. Есть и другие варианты.

Для описания поляризации пользуются вектором поляризации. Рассмотрим некоторый малый объем  диэлектрика. Тогда вектор поляризации определяется как сумма дипольных моментов всех молекул в этом объеме, деленная на величину объема:

,

где  — дипольный момент  - ой молекулы,  — число молекул в объеме. Опыт показывает, что связь между векторами  и  при малых полях линейна. Если среда изотропна, то эти векторы коллинеарны и можно написать

,

где  — коэффициент, зависящий от вещества диэлектрика.

Внешнее и внутреннее электрические поля векторно складываются и для описания вводится новый вектор , называемый электрическим смещением и определяемый следующей формулой:

,

где вектор  задает поле внутри диэлектрика. Если  и  коллинеарны, то связь между вектором смещения и вектором напряженности может быть записана в виде:

,

еде  называется диэлектрической проницаемостью диэлектрика. Для вакуума .

В кристалле направления векторов  и  не совпадают.