42,43 Потенциал электростатического поля. Потенциал точечного заряда. Консервативность электростатического поля
Неподвижный
точечный заряд
возбуждает
в вакууме электрическое поле
.
Пусть в этом поле перемещается другой
точечный заряд
,
переходя из начального положения 1 в
конечное положение 2 вдоль произвольной
кривой 12 (см. рис.). Работа, совершаемая
силами поля при таком перемещении,
выражается криволинейным интегралом
.
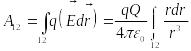Но
,
в чем легко убедится, дифференцируя
тождество
.
Поэтому криволинейный интеграл сводится
к определенному:
.
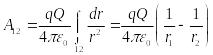Таким
образом, при любом выборе начальной и
конечной точек 1 и 2 работа
не
зависит от формы пути, а определяется
только положениями этих точек. Силовые
поля, удовлетворяющие такому условию,
называются потенциальными или
консервативными. Следовательно,
электростатическое поле точечного
заряда есть потенциальное поле.
Из принципа суперпозиции следует, что электрическое поле любой системы неподвижных зарядов потенциально. Как и в общем случае консервативных сил (см. раздел механика), можно показать, что работа по замкнутому пути равна нулю, и следовательно равна нулю циркуляция электростатического поля:
.
Это приводит к другому определению потенциальности поля. Векторное поле называется потенциальным, если циркуляция вектора по любому замкнутому контуру равна нулю.
Для
потенциальных полей можно ввести понятие
потенциала. Разностью потенциалов
между
точками 1 и 2 называется работа, совершаемая
силами поля при перемещении единичного
положительного заряда по произвольному
пути из точки 1 в точку 2. Потенциалу
какой-либо произвольной точки поля
можно
условно приписать любое значение
.
Потенциал любой другой точки определяется
однозначно. Однако, если поменять
,
то все остальные точки поменяют свой
потенциал тоже. Таким образом, потенциал
определен с точностью до аддитивной
постоянной.
Работа сил по перемещению заряда определяется выражением
.
В системе СИ потенциал измеряется в вольтах:
.
Если точки 1 и 2 расположены бесконечно близко, то можно найти связь потенциалом и напряженностью электрического поля. Формула выглядит следующим образом:
.
Выражение
в скобках есть вектор, называется
градиентом скаляра
и
обозначается
или
.
Если задана функция
,
то с помощью этой формулы можно вычислить
напряженность поля. Эта формула позволяет
ввести единицу для напряженности поля:
.
Вычислим потенциалы некоторых полей.
1. Потенциал поля точечного заряда в вакууме. Так как напряженность поля зависит только от радиуса, то уравнение связи напряженности и потенциала превращается в:
.
Отсюда после интегрирования
.
Обычно
константа равна нулю, так чтобы при
потенциал
обратился
в нуль.
2. Потенциал бесконечной равномерно заряженной плоскости.
Начало координат помещено на заряженной плоскости. Постоянная одна и та же в обоих выражениях, так как потенциал должен быть непрерывной функцией.
44 Проводники в электрическом поле.
1. Смещения электрических зарядов в металлах и изоляторах носят различный характер. В металлах есть свободные электроны, которые в пределах тела могут перемещаться как угодно. Воздействуя на проводник электрическим полем, можно разделить заряды и затем переместить заряды одного знака на другой объект.
2. Если бы внутри однородного проводника существовало макроскопическое электрическое поле, то оно привело бы в движение свободные электроны, т.е. задача стала бы не электростатической. Для равновесия необходимо, чтобы макроскопическое поле обращалось в нуль во всех точках внутри проводника. Кроме этого, объемная плотность заряда внутри однородного проводника равна нулю. Все заряды располагаются только на поверхности.
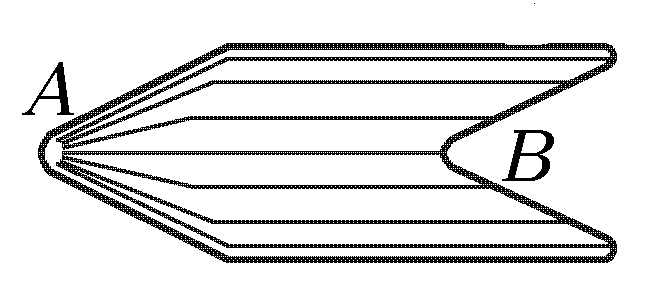
3. Распределение зарядов на поверхности проводника не обязательно однородно. Например, если зарядить тело, представленное на рисунке, то в точке плотность заряда будет значительно больше, чем в точке . Напряженность электрического поля и плотность силовых линий тоже. Кроме того, вектор напряженности перпендикулярен поверхности проводника. Если бы касательная составляющая не была равна нулю, то поверхностные заряды проводника пришли бы в движение, т.е. равновесие было бы невозможно. Величина нормальной составляющей напряженности с внешней стороны границы может быть получена при помощи теоремы Гаусса и равна:
.