
- •1 Кинематика материальной точки. Тело отсчета. Прямолинейное движение. Движение тела в пространстве. Декартова система координат. Система отсчета.
- •2 Радиус-вектор, скорость и ускорение материальной точки, их связь с декартовыми координатами.
- •3 Движение по криволинейной траектории. Тангенциальное и нормальное ускорения.
- •4 Кинематика твердого тела. Поступательное движение твердого тела. Вращение тела вокруг неподвижной оси. Угловая скорость вращения. Вектор угловой скорости. Угловое ускорение.
- •5 Первый закон Ньютона – закон инерции. Инерциальная система отсчета.
- •7 Третий закон Ньютона. Формулирование задачи движения материальных точек. Начальные условия.
- •10 Неинерциальные системы отсчета. Силы инерции.
- •11 Замкнутая система. Законы сохранения. Связь законов сохранения со свойствами пространства и времени.
- •12 Закон сохранения импульса
- •13 Момент силы и момент импульса относительно неподвижного начала. Их связь.
- •14 Закон сохранения момента импульса
- •15 Работа и кинетическая энергия
- •16 Консервативные и неконсервативные силы. Потенциальная энергия. Примеры потенциальной энергии.
- •17 Закон сохранения и изменения механической энергии
- •18 Абсолютно неупругий и абсолютно упругий удары.
- •19 Механика абсолютно твердого тела. Вращение вокруг неподвижной оси. Момент инерции.
- •20 Теорема Гюйгенса-Штейнера. Вычисление моментов инерции. Примеры.
- •21 Колебания. Разные типы колебаний.
- •22 Гармонические колебания. Основные характеристики колебательного процесса. Дифференциальное уравнение гармонических колебаний.
- •23 Пружинный маятник. Энергия маятника.
- •24 Физический маятник.
- •25 Затухающие колебания. Дифференциальное уравнение, вид решения, график,
- •26 Вынужденные колебания. Резонанс.
- •27 Волновые процессы. Уравнение плоской волны. Дифференциальное уравнение плоской волны.
- •28 Макроскопическая система большого количества молекул. Ее параметры. Равновесная система.
- •29 Массы и размеры молекул. Атомная масса. Молярная масса.
- •30 Уравнение идеального газа.
- •31 Распределение молекул по скоростям в идеальном газе.
- •32 Газ во внешнем потенциальном поле. Распределение Больцмана. Барометрическая формула.
- •33 Степени свободы. Теорема о равнораспределении энергии по степеням свободы.
- •34 Теплопередача. Макроскопическая работа. Первый закон (начало) термодинамики. Применение к изопроцессам.
- •35 Явления переноса. Средняя длина свободного пробега.
- •36 Диффузия.
- •37 Теплопроводность.
- •38 Взаимодействие зарядов. Их знаки. Единичный заряд. Закон Кулона.
- •39 Напряженность электростатического поля. Определение. Напряженность точечного заряда. Силовые линии.
- •41 Электрический диполь. Дипольный момент. Напряженность диполя на больших расстояниях.
- •41 Поток вектора и теорема Гаусса.
- •42,43 Потенциал электростатического поля. Потенциал точечного заряда. Консервативность электростатического поля
- •44 Проводники в электрическом поле.
- •45 Поляризация диэлектриков. Поляризуемость. Вектор электрического смещения. Электрическая проницаемость.
- •46 Электрический ток. Вектор плотности тока. Закон сохранения заряда в интегральном и дифференциальном виде.
- •47 Закон Ома в дифференциальном и интегральном виде. Удельная проводимость и удельное сопротивление.
- •48 Действие магнитного поля на проводники с током и движущиеся заряды.
- •49 Магнитное поле равномерно движущегося заряда. Закон Био—Савара.
- •50 Магнитное поле бесконечного прямого провода и витка с током.
- •51 Теорема Гаусса для магнитного поля. Циркуляция магнитного поля.
- •52 Магнитное поле в веществе. Различные типы магнетиков.
- •53 Емкость проводников и конденсаторов. Емкость шарового конденсатора.
- •54 Энергия заряженного конденсатора. Плотность электрической энергии. Энергия системы заряженных тел.
- •55 Электромагнитная индукция
- •56 Магнитный поток
- •57 Работа при перемещении витка с током в постоянном магнитном поле.
- •58 Самоиндукция. Коэффициенты индуктивности.
- •59 Энергия магнитного поля.
- •60 Ток смещения.
- •61 Система уравнений Максвелла.
- •62 Следствия из уравнений Максвелла.
- •63 Электромагнитные волны.
39 Напряженность электростатического поля. Определение. Напряженность точечного заряда. Силовые линии.
Электростатика изучает взаимодействие неподвижных зарядов. В классическом случае считается, что заряд некоторым образом изменяет свойства окружающего его пространства — создает электрическое поле. Основная характеристика поля должна зависеть только от величины заряда, создающего поле. Эта характеристика называется напряженностью и получается делением электростатической силы на заряд, на который действует поле:
![]() ,
,
где
![]() —
величина заряда, на который действует
поле. Для точеного заряда напряженность
получается из закона Кулона:
—
величина заряда, на который действует
поле. Для точеного заряда напряженность
получается из закона Кулона:
![]() .
.
Отношение
радиус-вектора
к
его величине выбирает (вместе со знаком
заряда) направление напряженности.
Напряженность электрического поля
нескольких неподвижных точечных зарядов
![]() равна
векторной сумме напряженностей полей,
которые создавал бы каждый из этих
зарядов в отсутствие остальных, т.е.
равна
векторной сумме напряженностей полей,
которые создавал бы каждый из этих
зарядов в отсутствие остальных, т.е.
![]() ,
,
где
![]() —
радиус-вектор, проведенный из заряда
—
радиус-вектор, проведенный из заряда
![]() в
точку наблюдения. Это положение называется
принципом суперпозиции электростатических
полей.
в
точку наблюдения. Это положение называется
принципом суперпозиции электростатических
полей.
Эта формула позволяет рассчитать напряженность электрического поля любой системы неподвижных зарядов. При непрерывном распределении зарядов сумма переходит в интеграл.
Для
изображения электрических полей
пользуются силовыми линиями. Силовая
линия есть математическая линия, в
каждой точке которой направление
касательной совпадает с направлением
вектора
![]() в
той же точке. Положительное направление
силовой линии совпадает с направлением
.
То есть силовые линии выходят из
положительных зарядов и оканчиваются
на отрицательных. Силовые линии идут
гуще там, где
сильнее.
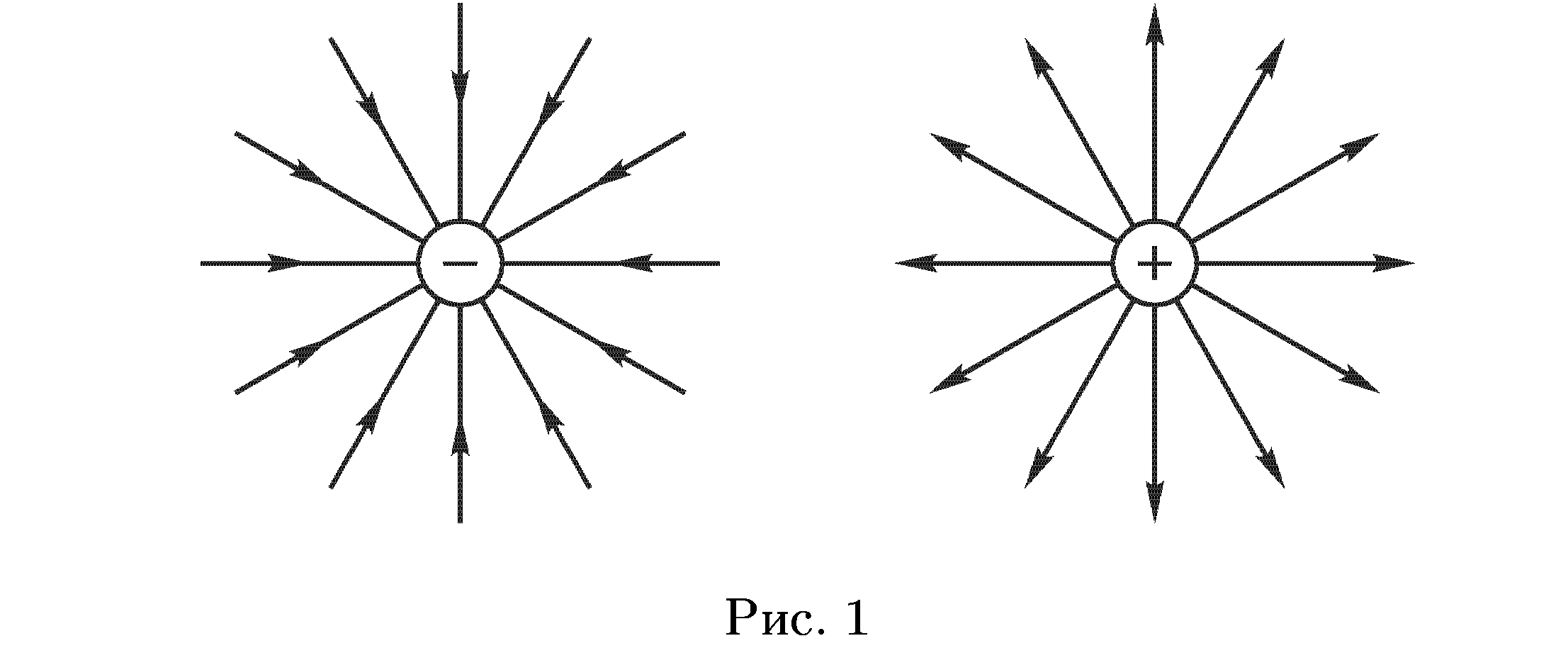
На рис. 1 изображены силовые линии
равномерно заряженных шариков —
положительного и отрицательного, а на
рис. 2 — двух разноименных и двух
одноименных зарядов равных величин.
в
той же точке. Положительное направление
силовой линии совпадает с направлением
.
То есть силовые линии выходят из
положительных зарядов и оканчиваются
на отрицательных. Силовые линии идут
гуще там, где
сильнее.
На рис. 1 изображены силовые линии
равномерно заряженных шариков —
положительного и отрицательного, а на
рис. 2 — двух разноименных и двух
одноименных зарядов равных величин.
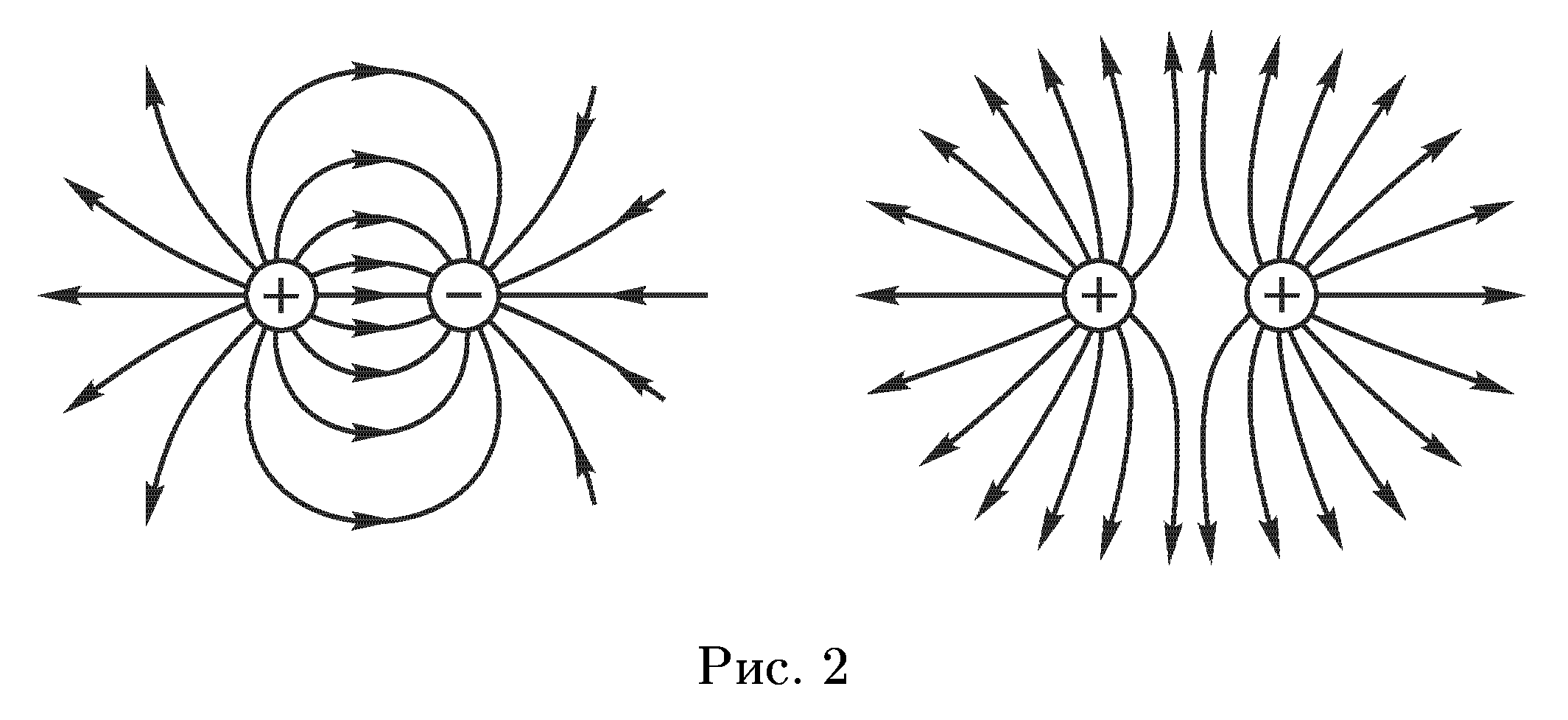
Получение этих кривых в общем случае требует решения системы дифференциальных уравнений в частных производных. Эти картинки можно получить экспериментально.
41 Электрический диполь. Дипольный момент. Напряженность диполя на больших расстояниях.
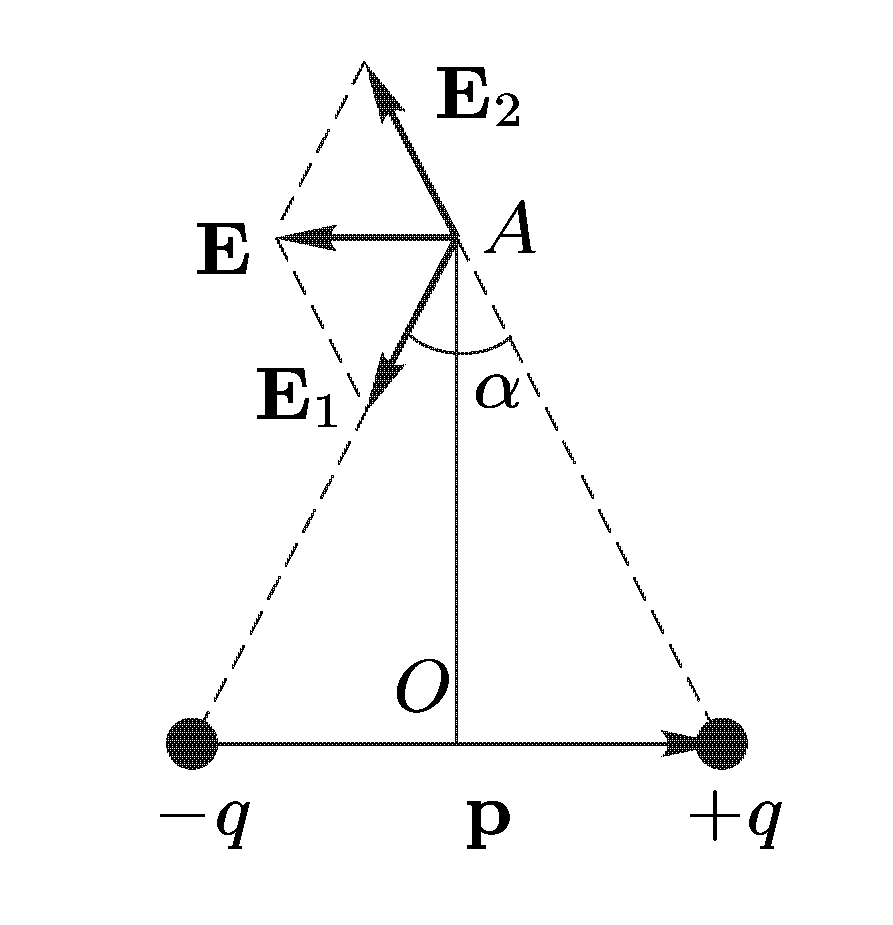
Простейшей
системой точечных зарядов является
электрический диполь. Так называется
система равных по величине, но
противоположных по знаку двух точечных
зарядов
![]() и
и
![]() ,
сдвинутых относительно друг друга на
некоторое расстояние (см рис.) Пусть
,
сдвинутых относительно друг друга на
некоторое расстояние (см рис.) Пусть
![]() —
вектор, проведенный от отрицательного
заряда к положительному. Вектор
—
вектор, проведенный от отрицательного
заряда к положительному. Вектор
![]() называется
электрическим моментом диполя или
дипольным моментом. Проведем радиус-вектор
от
точки
до
точки наблюдения. Тогда при
называется
электрическим моментом диполя или
дипольным моментом. Проведем радиус-вектор
от
точки
до
точки наблюдения. Тогда при
![]() величина
напряженности, создаваемой диполем в
точке наблюдения задается формулой
величина
напряженности, создаваемой диполем в
точке наблюдения задается формулой
![]() ,
,
где
![]() -
угол между
и
.
-
угол между
и
.
41 Поток вектора и теорема Гаусса.
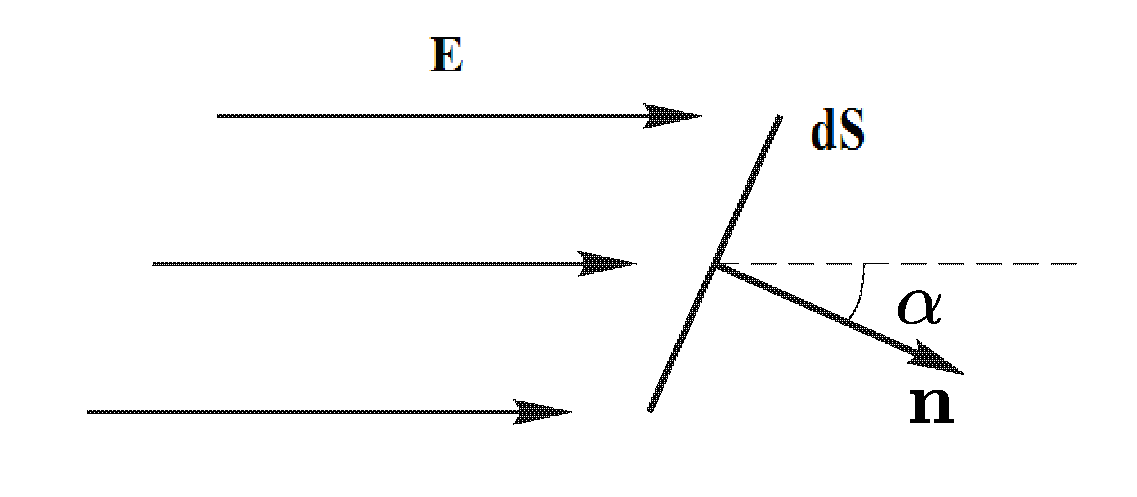
Потоком
вектора напряженности
через
малую площадку площадью
![]() называется
величина
называется
величина
![]() ,
,
где
—
угол между вектором
и
нормалью
к
площадке (см рис.). Если ввести вектор
![]() ,
то
,
то
![]() .
Если поверхность имеет сложную форму
и вектор
разный
в различных частях поверхности, то поток
напряженности
выражается
интегральной формулой
.
Если поверхность имеет сложную форму
и вектор
разный
в различных частях поверхности, то поток
напряженности
выражается
интегральной формулой
![]() .
.
Так как вектор напряженности от системы зарядов вычисляется по принципу суперпозиции, то поток полного вектора напряженности через заданную поверхность равнее сумме потоков через ту же поверхность каждого из векторов напряженности.
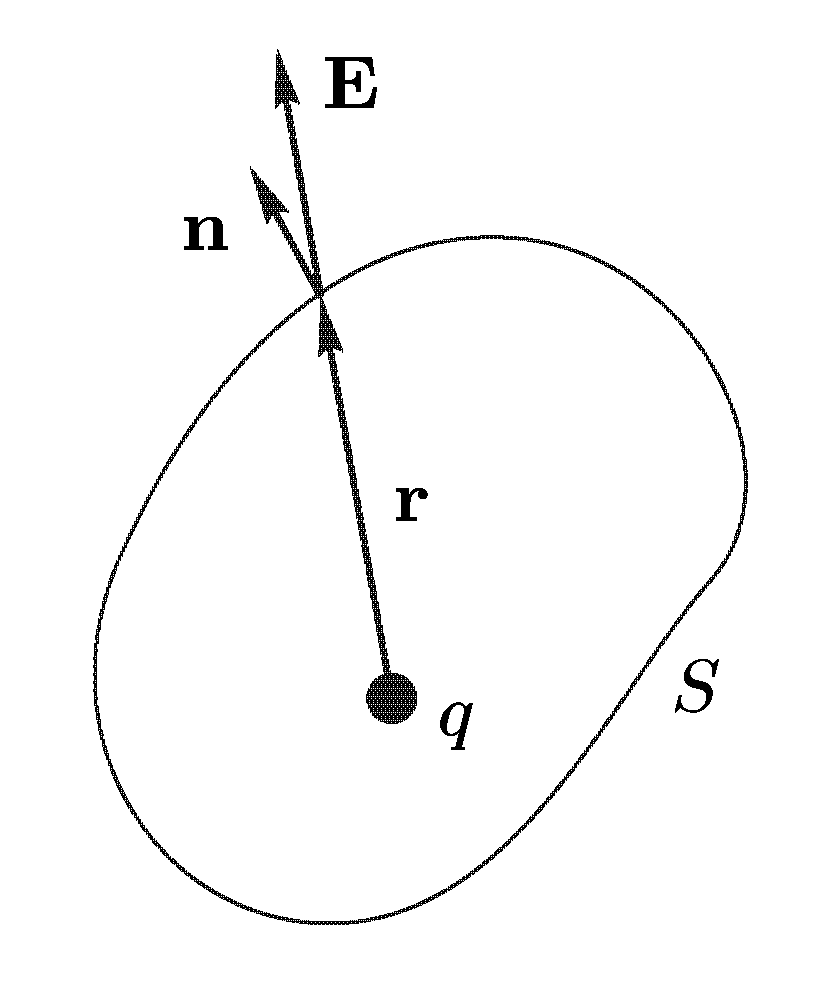
Перейдем
к теореме Гаусса. Она определяет поток
вектора через любую замкнутую поверхность
.
За положительную нормаль примем внешнюю
нормаль. Тогда можно доказать, что поток
![]() через
замкнутую поверхность выражается
формулой:
через
замкнутую поверхность выражается
формулой:
![]() ,
,
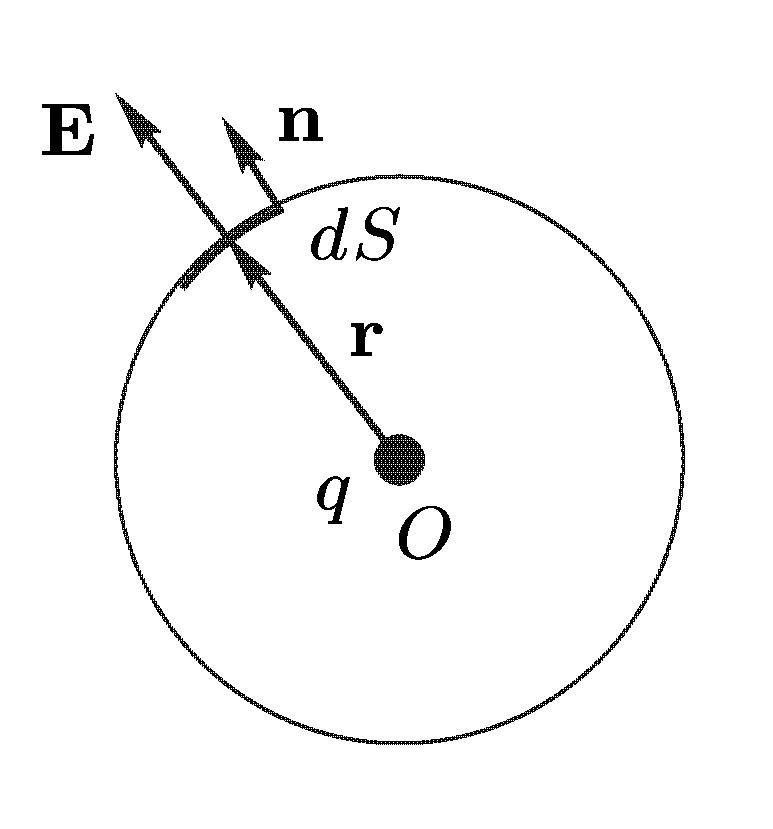
где все заряды в сумме находятся внутри объема, ограниченного замкнутой поверхностью (см. рис.). эту формулу легко получить, если поверхность является сферой, а один заряд расположен точно в центре сферы (см. след. рис.).
Теорема Гаусса выполняется для любого набора зарядов внутри объема и таким образом является хорошим уравнением для проверки вычислений электростатических полей. Однако, если система зарядов имеет симметрию, то теорему можно применять для вычисления этих полей. Покажем это на примере центрально симметричного расположения зарядов.
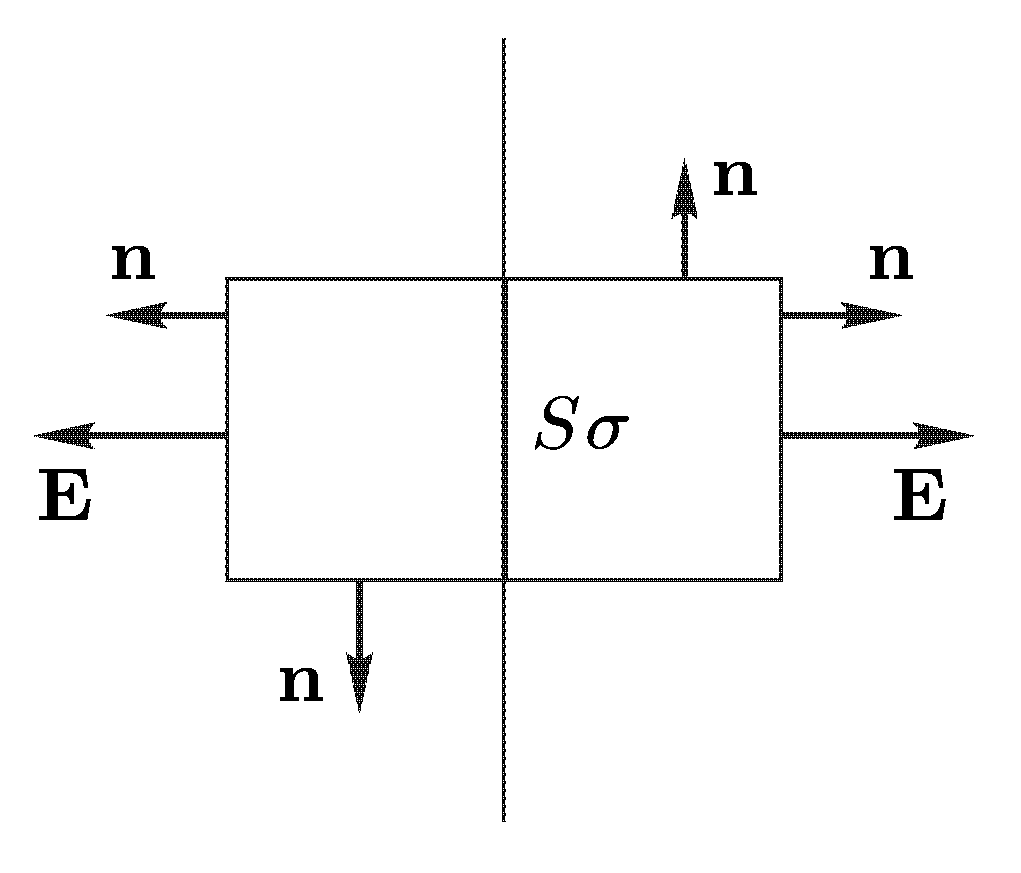
Пример. Электростатическое поле бесконечной равномерно заряженной плоскости.
Поверхностная
плотность заряда
постоянна.
Ввиду симметрии вектор
должен
быть перпендикулярен к этой плоскости.
Он направлен от плоскости, если она
заряжена положительно, и к плоскости,
если ее заряд отрицателен. Ввиду симметрии
длина вектора
может
зависеть только от расстояния до
заряженной плоскости, но не зависит от
того, с какой стороны находится точка
наблюдения. Построим цилиндр с основаниями,
симметрично расположенными по разные
стороны плоскости, и с образующими,
перпендикулярными к ней (см. рис.). Если
—
площадь основания, то поток вектора
через
одно основание равен
![]() ,
а через оба —
,
а через оба —
![]() .
Поток через боковую поверхность цилиндра
равен нулю, так как на ней векторы
и
взаимно
перпендикулярны. Поток через всю
поверхность цилиндра будет равен
.
Поток через боковую поверхность цилиндра
равен нулю, так как на ней векторы
и
взаимно
перпендикулярны. Поток через всю
поверхность цилиндра будет равен
![]() .
Используя теорему Гаусса, получаем:
.
Используя теорему Гаусса, получаем:
![]() .
.
Отсюда
![]() .
Величина напряженности не зависит от
расстояния.
.
Величина напряженности не зависит от
расстояния.
Много других симметричных задач можно решить подобным способом.
