32 Газ во внешнем потенциальном поле. Распределение Больцмана. Барометрическая формула.

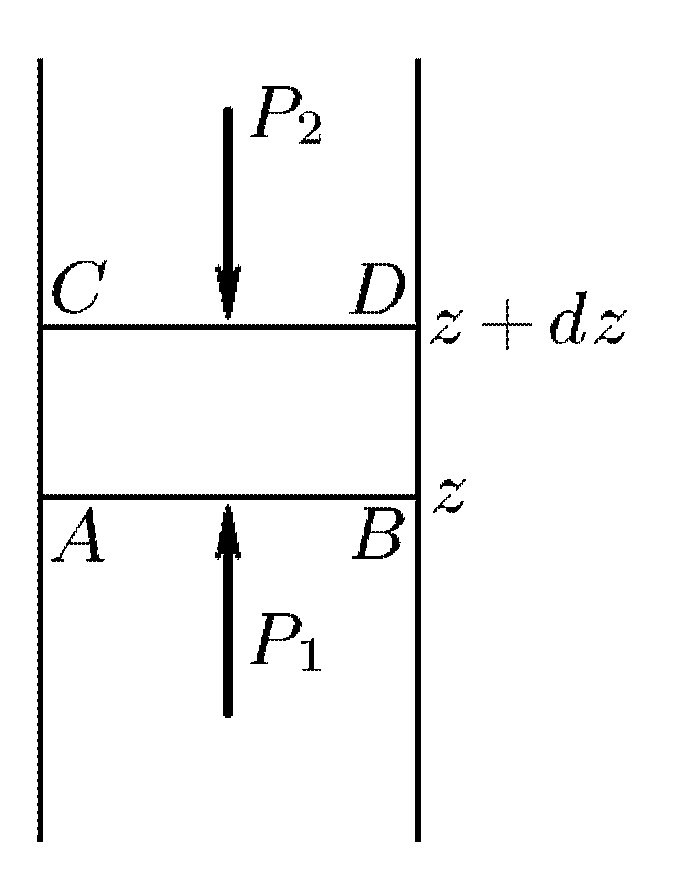
В отсутствие внешних сил концентрация молекул газа  в состоянии равновесия всюду одинакова. Но при наличии силовых полей это не так. Рассмотрим идеальный газ в однородном поле тяжести. В состоянии теплового равновесия температура  должна быть одинаковой по всей толщине газа. Найдем распределение концентрации по высоте. Направим ось  вверх. Выделим бесконечно короткий столб газа  (см. рис.) с высотой . Пусть площадь основания столба равна единице. Вес столба  должен уравновешиваться разностью давлений

.

Это приводит к соотношению

.

Подставляя сюда  и принимая во внимание, что температура  одинакова на всех высотах, получим

, или .

Аналогично можно получить формулу для любого неоднородного поля. В результате получится формула

,

где  — потенциальная энергия молекулы. Интегрируя, получаем

.

Это соотношение называется распределением Больцмана. Постоянная  — концентрация при .

Применительно к однородному полю тяжести, если от концентрации перейти к давлению , эта формула преобразуется в

.

Это — барометрическая формула.

 

 

Распределение энергии по степеням свободы. Теорема о равнораспределении энергии по степеням свободы. Внутренняя энергия идеального газа. Одноатомный, двухатомный и Многоатомный газы. Теплоемкость идеального газа.

Диффузия и теплопроводность. Неравновесные системы. Эволюция состояния неравновесных систем. Закон диффузии. Коэффициент диффузии. Уравнение сохранения числа частиц. Уравнение диффузии. Закон теплопроводности. Коэффициент теплопроводности.

 

33 Степени свободы. Теорема о равнораспределении энергии по степеням свободы.

 

Числом степеней свободы любого материального тела называется число величин, которые надо зафиксировать, чтобы полностью определить его положение. Чаще всего такими величинами являются координаты. Тогда у материальной точки в трехмерном пространстве число степеней свободы равно трем. Для любого тела число степеней свободы равно , где  — число материальных точек, образующих тело. Для абсолютно твердого тела задача упрощается. Так как все точки жестко связаны между собой, то достаточно задать три координаты центра инерции и три угла поворота относительно трех осей вращения, связанных с телом. Первые называются поступательными степенями свободы, а вторые вращательными.

Перейдем теперь к определению внутренней энергии простейшей системы — идеального газа. Все направления движения молекул идеального газа равновероятны. Поэтому можно предположить, что средние кинетические энергии по отдельным направлениям равны между собой, а также равны между собой средние кинетические энергии вращения относительно трех осей. Можно также показать, что для классического случая равны также средние кинетические энергии для поступательной степени свободы и для вращательной степени свободы. Для квантового случая последнее равенство выполняется не всегда. Теорема о равнораспределении энергии по степеням свободы еще дает величину средней энергии для каждой степени свободы в одном объекте: .

Молекулы газов бывают разные: одноатомные, двухатомные, трехатомные и многоатомные. Если не рассматривать внутреннюю структуру атома, т.е. взаимодействие электронов и ядра, то каждый атом в молекуле можно представить в в идее МТ. Кроме этого часто пренебрегают движением атомов внутри молекулы относительно друг друга (колебания). В этом случае нетрудно определить среднюю энергию, приходящуюся на одну молекулу идеального газа. В случае одноатомного газа на одну молекулу приходится средняя энергия, равная . В случае двухатомного газа таких степеней 5: 3 поступательных и 2 вращательных степени свободы (вращение относительно оси, проходящей через атомы не дает вклада в энергию). Средняя энергия: . В случае трех и многоатомного газа таких степеней столько же, сколько у твердого тела: 6, 3 поступательных и 3 вращательных степени свободы. Средняя энергия: . Общая формула , где  — число степеней свободы молекулы.

Следовательно, можно записать формулу для внутренней энергии идеального газа. Умножаем на полное число молекул:

Отсюда

 и

.

В классическом случае число степеней свободы не меняется с температурой. Однако, эксперимент и квантовая теория показывают обратное. При малых абсолютных температурах во внутреннюю энергию любого газа дают вклад только 3 поступательные степени свободы. При некоторой температуре включаются вращательные степени свободы. И, наконец, могут включиться колебательные степени свободы, для которых средний вклад во внутреннюю энергию молекулы вычисляется так . Это связано с тем, что при колебаниях усредняется не только кинетическая, но и потенциальная энергия.