30 Уравнение идеального газа.

Уравнение состояния заданной массы газа должно иметь вид

,

где  — давление,  — объем,  — термодинамическая температура. Единицей давления в СИ является паскаль (Па), равный Па=Н/м². Внесистемной единицей давления является «миллиметр ртутного столба», причем 1 мм.рт.ст.=133,3 Па. Стандартное атмосферное давление на поверхности Земли составляет примерно 0,1 МПа.

Термодинамическая температура , называемая также абсолютной, измеряется в кельвинах (К). Связь между ней и температурой , единицей которой является градус Цельсия ( ), имеет вид

Объем измеряется в м³.

Идеальным газом называется газ, параметры которого подчиняется уравнению Клапейрона—Менделеева:

.

Здесь  — масса газа,  — универсальная газовая постоянная. Это уравнение может быть преобразовано к некоторым другим видам. Наиболее важный получится, если обе уравнения разделить на объем и представить отношение число молей  в виде , где  — число молекул в газе. Определим теперь концентрацию  и уравнение преобразуется к виду

.

Отношение  называется постоянной Больцмана. Уравнение состояния еще более упрощается

.

Если рассматривать смесь различных идеальных газов (например, воздух), то надо сформулировать закон Дальтона. Пусть несколько идеальных газов занимают один и тот же объем (молекулы перемешиваются). Для каждого газа можно ввести свое отдельное давление, которое будет в этом газе, если бы всех остальных не было в объеме. Оно называется парциальным и в соответствии с уравнением идеального газа равно

,

где  — номер газа.

Дальтон экспериментально установил, что полное давление смеси равно сумме парциальных давлений

.

Кроме выше данного определения, ничего не говорящего о свойствах молекул газа, можно ввести физическое определение идеального газа. Идеальным газом называется газ, молекулы которого не взаимодействуют на расстоянии и при столкновении ведут себя абсолютно упруго. А суммарный объем всех молекул данного газа пренебрежимо мал по сравнению с объемом газа.

 

31 Распределение молекул по скоростям в идеальном газе.

Это распределение для идеального газа нашел теоретически Максвелл.

 

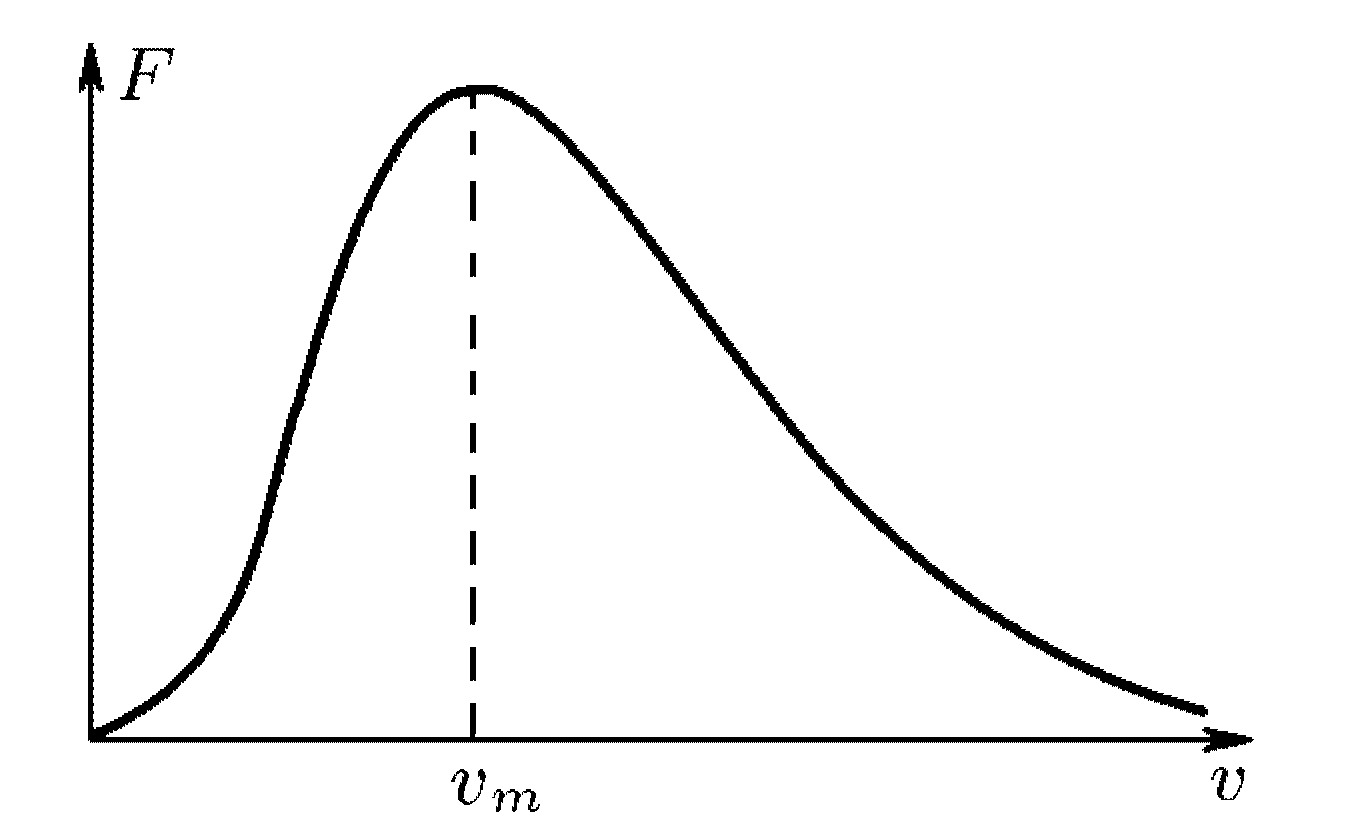Мы рассмотрим только распределение молекул по модулю их скорости.

Число молекул , имеющих модуль скорости (в дальнейшем просто скорости) в диапазоне от  до  может быть записано в виде

.

Здесь  — общее число молекул газа. Функция  называется функцией распределения молекул по скоростям. Эта по Максвеллу равна

.

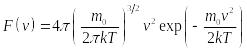Здесь   — масса молекулы газа.

Из рисунка видно, что функция имеет максимум в точке  (обычно называемой наиболее вероятностной  скоростью) и стремится к нулю на бесконечности. Эта функция может быть применена к газу, у которого очень много молекул. Величина  считается бесконечно малой. Для того, чтобы узнать количество молекул, имеющих скорость в не бесконечно малом диапазоне скоростей, надо воспользоваться интегральным исчислением:

,

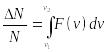где  и  — нижняя и верхняя границы скоростного диапазона.

Пользуясь этим распределением, можно получить необходимые для физиков величины средней, среднеквадратичной и наиболее вероятной скоростей.

Наиболее вероятная скорость получается, если взять производную от  и приравнять ее нулю. Получившееся уравнение приводит к

.

Любые средние величины вычисляются с помощью интегралов:

.

Вычисления приводят к следующим результатам:

,

.

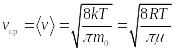Скорости хаотического движения молекул при обычных температурах велики. Например, для молекулы азота (азот главная составляющая воздуха), квадратичная скорость при 20⁰ С равна

.